2018-2019学年九年级数学下册单元测试(一)二次函数(B卷)(含答案)
文档属性
| 名称 | 2018-2019学年九年级数学下册单元测试(一)二次函数(B卷)(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 90.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-02 13:58:01 | ||
图片预览


文档简介
单元测试(一) 二次函数(B卷)
一、选择题(每小题3分,共30分)
1.抛物线y=-2x2+1的对称轴是(C)
A.直线x= B.直线x=-
C.y轴 D.直线x=2
2.将二次函数y=x2-2x+3化为y=(x-h)2+k的形式,结果为(D)
A.y=(x+1)2+4 B.y=(x+1)2+2
C.y=(x-1)2+4 D.y=(x-1)2+2
3.若函数y=axa2-2a-6是二次函数且图象开口向上,则a=(B)
A.-2 B.4
C.4或-2 D.4或3
4.顶点为(5,1),形状与函数y=x2的图象相同且开口方向相反的抛物线是(A)
A.y=-(x-5)2+1 B.y=-x2-5
C.y=-(x-5)2-1 D.y=(x+5)2-1
5.二次函数y=(x-2)2+3是由二次函数y=x2怎样平移得到的(A)
A.向右平移2个单位长度,向上平移3个单位长度
B.向左平移2个单位长度,向上平移3个单位长度
C.向右平移3个单位长度,向上平移2个单位长度
D.向右平移2个单位长度,向下平移3个单位长度
6.若二次函数y=x2-mx+1的图象的顶点在x轴上,则m的值是(D)
A.2 B.-2
C.0 D.±2
7.若二次函数y=ax2+bx+c(a<0)的图象经过点(2,0),且其对称轴为直线x=-1,则使函数值y>0成立的x的取值范围是(D)
A.x<-4或x>2 B.-4≤x≤2
C.x≤-4或x≥2 D.-48.已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式h=-t2+24t+1.则下列说法中正确的是(D)
A.点火后9 s和点火后13 s的升空高度相同
B.点火后24 s火箭落于地面
C.点火后10 s的升空高度为139 m
D.火箭升空的最大高度为145 m
9.当ab>0时,y=ax2与y=ax+b的图象大致是(D)
A B C D
10.如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A,B的横坐标分别为-1和3,则下列结论正确的是(D)
A.2a-b=0
B.a+b+c>0
C.3a-c=0
D.当a=时,△ABD是等腰直角三角形
二、填空题(每小题4分,共24分)
11.若函数y=x2+2x-m的图象与x轴有且只有一个交点,则m的值为-1.
12.如果点A(-2,y1)和点B(2,y2)是抛物线y=(x+3)2上的两点,那么 y1<y2(填“>”“=”或“<”).
13.已知函数y=ax2+bx+c,当x=3时,函数取最大值4,当x=0时,y=-14,则函数表达式为y=-2(x-3)2+4.
14.某旅行社组团去外地旅游,30人起组团,每人单价800元.旅行社对超过30人的团给予优惠,即旅行团的人数每增加一人,每人的单价就降低10元.当一个旅行团的人数是55人时,这个旅行社可以获得最大的营业额.
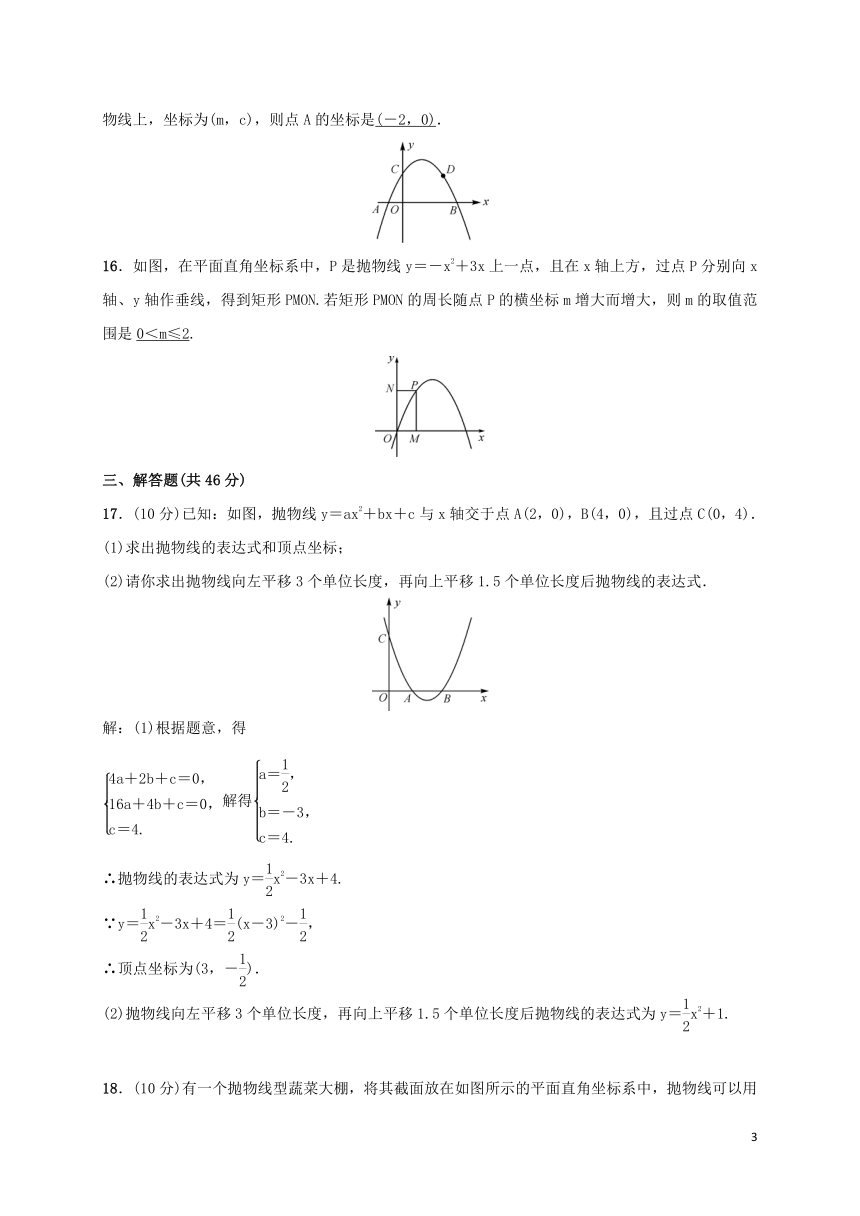
15.如图,抛物线y=ax2+bx+c与x轴相交于点A,B(m+2,0),与y轴相交于点C,点D在该抛物线上,坐标为(m,c),则点A的坐标是(-2,0).
16.如图,在平面直角坐标系中,P是抛物线y=-x2+3x上一点,且在x轴上方,过点P分别向x轴、y轴作垂线,得到矩形PMON.若矩形PMON的周长随点P的横坐标m增大而增大,则m的取值范围是0<m≤2.
三、解答题(共46分)
17.(10分)已知:如图,抛物线y=ax2+bx+c与x轴交于点A(2,0),B(4,0),且过点C(0,4).
(1)求出抛物线的表达式和顶点坐标;
(2)请你求出抛物线向左平移3个单位长度,再向上平移1.5个单位长度后抛物线的表达式.
解:(1)根据题意,得
解得
∴抛物线的表达式为y=x2-3x+4.
∵y=x2-3x+4=(x-3)2-,
∴顶点坐标为(3,-).
(2)抛物线向左平移3个单位长度,再向上平移1.5个单位长度后抛物线的表达式为y=x2+1.
18.(10分)有一个抛物线型蔬菜大棚,将其截面放在如图所示的平面直角坐标系中,抛物线可以用函数y=ax2+bx来表示.已知大棚在地面上的宽度OA为8米,距离O点2米处的棚高BC为米.
(1)求该抛物线的函数关系式;
(2)若借助横梁DE建一个门,要求门的高度不低于1.5米,则横梁DE的宽度最多是多少米?
解:(1)由题意可得,抛物线经过(2,),(8,0),
∴
解得∴y=-x2+x.
(2)由题意可得:当y=1.5时,1.5=-x2+x,
解得x1=4+2,x2=4-2.
故DE=|x1-x2|=|4+2-(4-2)|=4.
即横梁DE的宽度最多是4米.
19.(12分)如图,矩形ABCD的两边长AB=18 cm,AD=4 cm,点P,Q分别从A,B同时出发,P在边AB上沿AB方向以2 cm/s的速度匀速运动,Q在边BC上沿BC方向以1 cm/s的速度匀速运动,当一点到达终点时,另一点也停止运动.设运动时间为x s,△PBQ的面积为y(cm2).
(1)求y关于x的函数表达式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.
解:(1)∵S△PBQ=PB·BQ,
PB=AB-AP=18-2x,BQ=x,
∴y=x(18-2x),
即y=-x2+9x(0(2)由(1)知y=-x2+9x,
∴y=-(x-)2+.
∵当0<x≤时,y随x的增大而增大,而0∴当x=4时,y最大=20,即△PBQ的最大面积是20 cm2.
20.(14分)如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.
(1)求二次函数y=ax2+bx+4的表达式;
(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,求OM与AC的数量关系.
解:(1)将点B,C的坐标分别代入y=ax2+bx+4,得
解得
∴二次函数的表达式为y=-x2+x+4.
(2)设点N的坐标为(n,0)(-2<n<8),则BN=n+2,CN=8-n.
∵B(-2,0),C(8,0),∴BC=10.
在y=-x2+x+4中,令x=0,则y=4.
∴A(0,4),OA=4.
∴S△ABN=BN·OA=(n+2)×4=2(n+2).
∵MN∥AC,∴==.
∴==,
∴S△AMN=S△ABN=(8-n)(n+2)=-(n-3)2+5.
∵-<0,∴当n=3时,即N(3,0)时,△AMN的面积最大.
(3)当N(3,0)时,N为BC边的中点.
∵MN∥AC,∴M为AB边中点.∴OM=AB.
∵AB==2,AC==4,
∴AB=AC.∴OM=AC.
一、选择题(每小题3分,共30分)
1.抛物线y=-2x2+1的对称轴是(C)
A.直线x= B.直线x=-
C.y轴 D.直线x=2
2.将二次函数y=x2-2x+3化为y=(x-h)2+k的形式,结果为(D)
A.y=(x+1)2+4 B.y=(x+1)2+2
C.y=(x-1)2+4 D.y=(x-1)2+2
3.若函数y=axa2-2a-6是二次函数且图象开口向上,则a=(B)
A.-2 B.4
C.4或-2 D.4或3
4.顶点为(5,1),形状与函数y=x2的图象相同且开口方向相反的抛物线是(A)
A.y=-(x-5)2+1 B.y=-x2-5
C.y=-(x-5)2-1 D.y=(x+5)2-1
5.二次函数y=(x-2)2+3是由二次函数y=x2怎样平移得到的(A)
A.向右平移2个单位长度,向上平移3个单位长度
B.向左平移2个单位长度,向上平移3个单位长度
C.向右平移3个单位长度,向上平移2个单位长度
D.向右平移2个单位长度,向下平移3个单位长度
6.若二次函数y=x2-mx+1的图象的顶点在x轴上,则m的值是(D)
A.2 B.-2
C.0 D.±2
7.若二次函数y=ax2+bx+c(a<0)的图象经过点(2,0),且其对称轴为直线x=-1,则使函数值y>0成立的x的取值范围是(D)
A.x<-4或x>2 B.-4≤x≤2
C.x≤-4或x≥2 D.-4
A.点火后9 s和点火后13 s的升空高度相同
B.点火后24 s火箭落于地面
C.点火后10 s的升空高度为139 m
D.火箭升空的最大高度为145 m
9.当ab>0时,y=ax2与y=ax+b的图象大致是(D)
A B C D
10.如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A,B的横坐标分别为-1和3,则下列结论正确的是(D)
A.2a-b=0
B.a+b+c>0
C.3a-c=0
D.当a=时,△ABD是等腰直角三角形
二、填空题(每小题4分,共24分)
11.若函数y=x2+2x-m的图象与x轴有且只有一个交点,则m的值为-1.
12.如果点A(-2,y1)和点B(2,y2)是抛物线y=(x+3)2上的两点,那么 y1<y2(填“>”“=”或“<”).
13.已知函数y=ax2+bx+c,当x=3时,函数取最大值4,当x=0时,y=-14,则函数表达式为y=-2(x-3)2+4.
14.某旅行社组团去外地旅游,30人起组团,每人单价800元.旅行社对超过30人的团给予优惠,即旅行团的人数每增加一人,每人的单价就降低10元.当一个旅行团的人数是55人时,这个旅行社可以获得最大的营业额.
15.如图,抛物线y=ax2+bx+c与x轴相交于点A,B(m+2,0),与y轴相交于点C,点D在该抛物线上,坐标为(m,c),则点A的坐标是(-2,0).
16.如图,在平面直角坐标系中,P是抛物线y=-x2+3x上一点,且在x轴上方,过点P分别向x轴、y轴作垂线,得到矩形PMON.若矩形PMON的周长随点P的横坐标m增大而增大,则m的取值范围是0<m≤2.
三、解答题(共46分)
17.(10分)已知:如图,抛物线y=ax2+bx+c与x轴交于点A(2,0),B(4,0),且过点C(0,4).
(1)求出抛物线的表达式和顶点坐标;
(2)请你求出抛物线向左平移3个单位长度,再向上平移1.5个单位长度后抛物线的表达式.
解:(1)根据题意,得
解得
∴抛物线的表达式为y=x2-3x+4.
∵y=x2-3x+4=(x-3)2-,
∴顶点坐标为(3,-).
(2)抛物线向左平移3个单位长度,再向上平移1.5个单位长度后抛物线的表达式为y=x2+1.
18.(10分)有一个抛物线型蔬菜大棚,将其截面放在如图所示的平面直角坐标系中,抛物线可以用函数y=ax2+bx来表示.已知大棚在地面上的宽度OA为8米,距离O点2米处的棚高BC为米.
(1)求该抛物线的函数关系式;
(2)若借助横梁DE建一个门,要求门的高度不低于1.5米,则横梁DE的宽度最多是多少米?
解:(1)由题意可得,抛物线经过(2,),(8,0),
∴
解得∴y=-x2+x.
(2)由题意可得:当y=1.5时,1.5=-x2+x,
解得x1=4+2,x2=4-2.
故DE=|x1-x2|=|4+2-(4-2)|=4.
即横梁DE的宽度最多是4米.
19.(12分)如图,矩形ABCD的两边长AB=18 cm,AD=4 cm,点P,Q分别从A,B同时出发,P在边AB上沿AB方向以2 cm/s的速度匀速运动,Q在边BC上沿BC方向以1 cm/s的速度匀速运动,当一点到达终点时,另一点也停止运动.设运动时间为x s,△PBQ的面积为y(cm2).
(1)求y关于x的函数表达式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.
解:(1)∵S△PBQ=PB·BQ,
PB=AB-AP=18-2x,BQ=x,
∴y=x(18-2x),
即y=-x2+9x(0
∴y=-(x-)2+.
∵当0<x≤时,y随x的增大而增大,而0
20.(14分)如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.
(1)求二次函数y=ax2+bx+4的表达式;
(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,求OM与AC的数量关系.
解:(1)将点B,C的坐标分别代入y=ax2+bx+4,得
解得
∴二次函数的表达式为y=-x2+x+4.
(2)设点N的坐标为(n,0)(-2<n<8),则BN=n+2,CN=8-n.
∵B(-2,0),C(8,0),∴BC=10.
在y=-x2+x+4中,令x=0,则y=4.
∴A(0,4),OA=4.
∴S△ABN=BN·OA=(n+2)×4=2(n+2).
∵MN∥AC,∴==.
∴==,
∴S△AMN=S△ABN=(8-n)(n+2)=-(n-3)2+5.
∵-<0,∴当n=3时,即N(3,0)时,△AMN的面积最大.
(3)当N(3,0)时,N为BC边的中点.
∵MN∥AC,∴M为AB边中点.∴OM=AB.
∵AB==2,AC==4,
∴AB=AC.∴OM=AC.
