2018-2019学年九年级数学下册单元测试(一)二次函数(A卷)(含答案)
文档属性
| 名称 | 2018-2019学年九年级数学下册单元测试(一)二次函数(A卷)(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 150.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-02 13:59:10 | ||
图片预览

文档简介
单元测试(一) 二次函数(A卷)
一、选择题(每小题3分,共30分)
1.下列各式中,y是x的二次函数的是(B)
A.xy+x2=1 B.x2-y+2=0
C.y= D.y2-4x=3
2.抛物线y=(x-1)2+1的顶点坐标为(A)
A.(1,1) B.(1,-1)
C.(-1,1) D.(-1,-1)
3.将二次函数y=x2-4x-4化为y=a(x-h)2+k的形式,正确的是(D)
A.y=(x-2)2 B.y=(x+2)2-8
C.y=(x+2)2 D.y=(x-2)2-8
4.抛物线y=2x2向右平移3个单位长度,再向下平移5个单位长度,得到的抛物线的表达式为(A)
A.y=2(x-3)2-5 B.y=2(x+3)2+5
C.y=2(x-3)2+5 D.y=2(x+3)2-5
5.关于函数y=3x2的性质的叙述,错误的是(B)
A.顶点是原点
B.y有最大值
C.当x>0时,y随x的增大而增大
D.当x<0时,y随x的增大而减小
6.在平面直角坐标系中,二次函数y=a(x-h)2(a≠0)的图象可能是(D)
A B C D
7.小颖用计算器探索方程ax2+bx+c=0的根,作出如图所示的图象,并求得一个近似根x=-3.4,则方程的另一个近似根为(精确到0.1)(D)
A.4.4 B.3.4 C.2.4 D.1.4
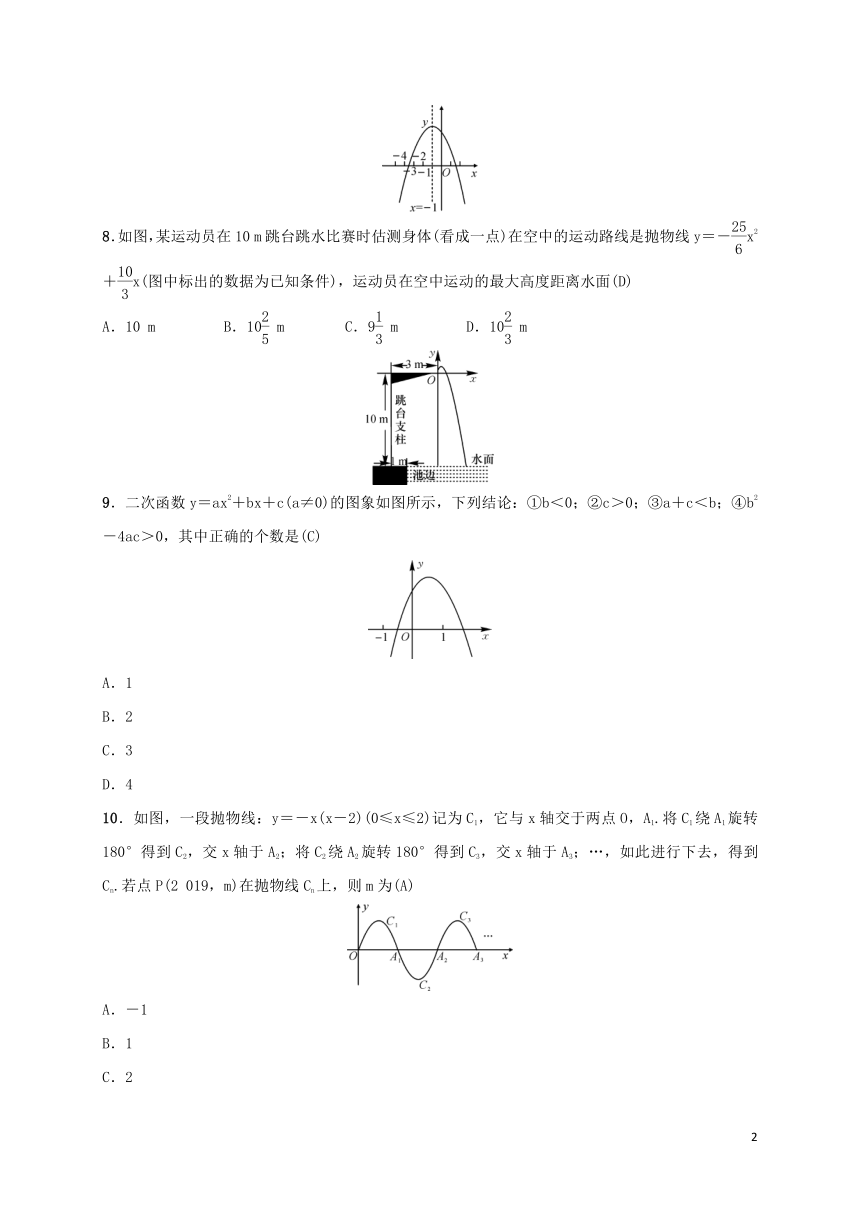
8.如图,某运动员在10 m跳台跳水比赛时估测身体(看成一点)在空中的运动路线是抛物线y=-x2+x(图中标出的数据为已知条件),运动员在空中运动的最大高度距离水面(D)
A.10 m B.10 m C.9 m D.10 m
9.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b<0;②c>0;③a+c<b;④b2-4ac>0,其中正确的个数是(C)
A.1
B.2
C.3
D.4
10.如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1,它与x轴交于两点O,A1.将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…,如此进行下去,得到Cn.若点P(2 019,m)在抛物线Cn上,则m为(A)
A.-1
B.1
C.2
D.3
二、填空题(每小题4分,共24分)
11.抛物线y=(x-1)2+5与y轴交点的坐标是(0,6).
12.已知抛物线y=ax2-3x+c(a≠0)经过点(-2,4),则4a+c-1=-3.
13.如图,已知二次函数y=x2-4x-5与x轴交于A,B两点,则AB的长度为6.
14.已知点A(x1,y1),B(x2,y2)在二次函数y=-x2-2x的图象上.若x1>x2>-1,则y1<y2.(填“>”“<”或“=”)
15.出售某种文具盒,若每个获利x元,一天可售出(6-x)个,则当x=3元时,一天出售该种文具盒的总利润最大.
16.某学习小组为了探究函数y=x2-|x|的图象和性质,根据以往学习函数的经验,列表确定了该函数图象上一些点的坐标,表格中的m=__0.75.
x
…
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
…
y
…
2
0.75
0
-0.25
0
-0.25
0
m
2
…
三、解答题(共46分)
17.(10分)已知抛物线y=3x2-2x+4.
(1)通过配方,将抛物线的表达式写成y=a(x-h)2+k的形式;
(2)写出抛物线的开口方向和对称轴.
解:(1)y=3x2-2x+4=3[x2-x+()2-()2]+4=3(x-)2-+4=3(x-)2+.
(2)开口向上,对称轴是直线x=.
18.(10分)已知抛物线y=-x2+2(m-1)x+m+1.
(1)求证:无论m取何值,抛物线与x轴总有两个不同的交点;
(2)若抛物线与x轴交于A,B两点,且A点在原点的右边,B点在原点的左边,求m的取值范围.
解:(1)证明:∵b2-4ac=[2(m-1)]2-4×(-1)×(m+1)=(2m-1)2+7>0,
∴抛物线与x轴总有两个不同的交点.
(2)设A(x1,0),B(x2,0),则x1>0,x2<0,
∴x1x2=-(m+1)<0.
∴m>-1.
19.(12分)投资1万元围一个矩形菜园(如图),其中一边靠墙,另外三边选用不同材料建造.墙长24 m,平行于墙的边的费用为200元/m,垂直于墙的边的费用为150元/m,设平行于墙的边长为x m.
(1)设垂直于墙的一边长为y m,直接写出y与x之间的函数关系式;
(2)若菜园面积为384 m2,求x的值;
(3)求菜园的最大面积.
解:(1)根据题意知,y==-x+.
(2)根据题意,得(-x+)x=384,
解得x=18或x=32.
∵墙的长度为24 m,∴x=18.
(3)设菜园的面积是S,则S=(-x+)x=-(x-25)2+.
∵-<0,∴当x<25时,S随x的增大而增大.
∵x≤24,
∴当x=24时,S取得最大值,最大值为416.
答:菜园的最大面积为416 m2.
20.(14分)如图,顶点为(,-)的抛物线y=ax2+bx+c过点M(2,0).
(1)求抛物线的表达式;
(2)点A是抛物线与x轴的交点(不与点M重合),点B是抛物线与y轴的交点,点C是直线y=x+1上一点(处于x轴下方),点D是反比例函数y=(k>0)图象上一点,若以点A,B,C,D为顶点的四边形是菱形,求k的值.
解:(1)依题意可设抛物线为y=a(x-)2-,将点M(2,0)代入,得
a(2-)2-=0,解得a=1.
∴抛物线的表达式为y=(x-)2-.
(2)当y=0时,(x-)2-=0,
解得x1=-1,x2=2,∴A(-1,0).
当x=0时,y=(x-)2-=-2,∴B(0,-2).
在Rt△OAB中,OA=1,OB=2,∴AB=.
设直线y=x+1与y轴的交点为G,易求G(0,1),
∴Rt△AOG为等腰直角三角形.∴∠AGO=45°.
∵点C在y=x+1上且在x轴下方,而k>0,所以y=的图象位于第一、第三象限,故点D只能在第一、第三象限,因而符合条件的菱形中有如下两种情况:
①此菱形以AB为边且AC也为边,如图1所示,k=+.
②此菱形以AB为对角线,如图2所示,k=.
图1 图2
一、选择题(每小题3分,共30分)
1.下列各式中,y是x的二次函数的是(B)
A.xy+x2=1 B.x2-y+2=0
C.y= D.y2-4x=3
2.抛物线y=(x-1)2+1的顶点坐标为(A)
A.(1,1) B.(1,-1)
C.(-1,1) D.(-1,-1)
3.将二次函数y=x2-4x-4化为y=a(x-h)2+k的形式,正确的是(D)
A.y=(x-2)2 B.y=(x+2)2-8
C.y=(x+2)2 D.y=(x-2)2-8
4.抛物线y=2x2向右平移3个单位长度,再向下平移5个单位长度,得到的抛物线的表达式为(A)
A.y=2(x-3)2-5 B.y=2(x+3)2+5
C.y=2(x-3)2+5 D.y=2(x+3)2-5
5.关于函数y=3x2的性质的叙述,错误的是(B)
A.顶点是原点
B.y有最大值
C.当x>0时,y随x的增大而增大
D.当x<0时,y随x的增大而减小
6.在平面直角坐标系中,二次函数y=a(x-h)2(a≠0)的图象可能是(D)
A B C D
7.小颖用计算器探索方程ax2+bx+c=0的根,作出如图所示的图象,并求得一个近似根x=-3.4,则方程的另一个近似根为(精确到0.1)(D)
A.4.4 B.3.4 C.2.4 D.1.4
8.如图,某运动员在10 m跳台跳水比赛时估测身体(看成一点)在空中的运动路线是抛物线y=-x2+x(图中标出的数据为已知条件),运动员在空中运动的最大高度距离水面(D)
A.10 m B.10 m C.9 m D.10 m
9.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b<0;②c>0;③a+c<b;④b2-4ac>0,其中正确的个数是(C)
A.1
B.2
C.3
D.4
10.如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1,它与x轴交于两点O,A1.将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…,如此进行下去,得到Cn.若点P(2 019,m)在抛物线Cn上,则m为(A)
A.-1
B.1
C.2
D.3
二、填空题(每小题4分,共24分)
11.抛物线y=(x-1)2+5与y轴交点的坐标是(0,6).
12.已知抛物线y=ax2-3x+c(a≠0)经过点(-2,4),则4a+c-1=-3.
13.如图,已知二次函数y=x2-4x-5与x轴交于A,B两点,则AB的长度为6.
14.已知点A(x1,y1),B(x2,y2)在二次函数y=-x2-2x的图象上.若x1>x2>-1,则y1<y2.(填“>”“<”或“=”)
15.出售某种文具盒,若每个获利x元,一天可售出(6-x)个,则当x=3元时,一天出售该种文具盒的总利润最大.
16.某学习小组为了探究函数y=x2-|x|的图象和性质,根据以往学习函数的经验,列表确定了该函数图象上一些点的坐标,表格中的m=__0.75.
x
…
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
…
y
…
2
0.75
0
-0.25
0
-0.25
0
m
2
…
三、解答题(共46分)
17.(10分)已知抛物线y=3x2-2x+4.
(1)通过配方,将抛物线的表达式写成y=a(x-h)2+k的形式;
(2)写出抛物线的开口方向和对称轴.
解:(1)y=3x2-2x+4=3[x2-x+()2-()2]+4=3(x-)2-+4=3(x-)2+.
(2)开口向上,对称轴是直线x=.
18.(10分)已知抛物线y=-x2+2(m-1)x+m+1.
(1)求证:无论m取何值,抛物线与x轴总有两个不同的交点;
(2)若抛物线与x轴交于A,B两点,且A点在原点的右边,B点在原点的左边,求m的取值范围.
解:(1)证明:∵b2-4ac=[2(m-1)]2-4×(-1)×(m+1)=(2m-1)2+7>0,
∴抛物线与x轴总有两个不同的交点.
(2)设A(x1,0),B(x2,0),则x1>0,x2<0,
∴x1x2=-(m+1)<0.
∴m>-1.
19.(12分)投资1万元围一个矩形菜园(如图),其中一边靠墙,另外三边选用不同材料建造.墙长24 m,平行于墙的边的费用为200元/m,垂直于墙的边的费用为150元/m,设平行于墙的边长为x m.
(1)设垂直于墙的一边长为y m,直接写出y与x之间的函数关系式;
(2)若菜园面积为384 m2,求x的值;
(3)求菜园的最大面积.
解:(1)根据题意知,y==-x+.
(2)根据题意,得(-x+)x=384,
解得x=18或x=32.
∵墙的长度为24 m,∴x=18.
(3)设菜园的面积是S,则S=(-x+)x=-(x-25)2+.
∵-<0,∴当x<25时,S随x的增大而增大.
∵x≤24,
∴当x=24时,S取得最大值,最大值为416.
答:菜园的最大面积为416 m2.
20.(14分)如图,顶点为(,-)的抛物线y=ax2+bx+c过点M(2,0).
(1)求抛物线的表达式;
(2)点A是抛物线与x轴的交点(不与点M重合),点B是抛物线与y轴的交点,点C是直线y=x+1上一点(处于x轴下方),点D是反比例函数y=(k>0)图象上一点,若以点A,B,C,D为顶点的四边形是菱形,求k的值.
解:(1)依题意可设抛物线为y=a(x-)2-,将点M(2,0)代入,得
a(2-)2-=0,解得a=1.
∴抛物线的表达式为y=(x-)2-.
(2)当y=0时,(x-)2-=0,
解得x1=-1,x2=2,∴A(-1,0).
当x=0时,y=(x-)2-=-2,∴B(0,-2).
在Rt△OAB中,OA=1,OB=2,∴AB=.
设直线y=x+1与y轴的交点为G,易求G(0,1),
∴Rt△AOG为等腰直角三角形.∴∠AGO=45°.
∵点C在y=x+1上且在x轴下方,而k>0,所以y=的图象位于第一、第三象限,故点D只能在第一、第三象限,因而符合条件的菱形中有如下两种情况:
①此菱形以AB为边且AC也为边,如图1所示,k=+.
②此菱形以AB为对角线,如图2所示,k=.
图1 图2
