运动快慢的描述（二）

(共17张PPT)
运动快慢的描述（二）
刘翔在110米栏的竞赛中，前半程速度与后半程速度是否一样？
一辆汽车10s内向东行驶120m，另一辆汽车向西行驶120m，比较这两种情况下的平均速度的大小和方向。
参考：
平均速度的大小相等，但方向不同。所以它们的平均速度不同。
三、平均速度和瞬时速度
(1)平均速度
在变速直线运动中，运动物体的位移和所用时间的比值，叫做这段时间内（或这段位移内）的平均速度。
△x
△t
υ=
-
平均速度只是粗略的描述变速运动的快慢。△t 越小，平均速度越接近质点运动的真实速度，描述越精确。
三、平均速度和瞬时速度
(1)平均速度
对于变速直线运动，不同时间内（或不同位移上）的平均速度的值可能不一样。所以提到平均速度必须要指明是哪一段时间或哪一段位移内的平均速度。
平均速度是矢量，方向与这段时间内发生的位移方向相同。
平均速度概念与速度的平均值概念是完全不相同的。
一物体做同向直线运动，前一半时间以速度υ1匀速运动，后一半时间以速度υ2 匀速运动，则该物体的平均速度为多少？另一物体也做同向直线运动，前一半路程以速度υ1匀速运动，后一半路程以速度υ2匀速运动，则该物体的平均速度为多大？
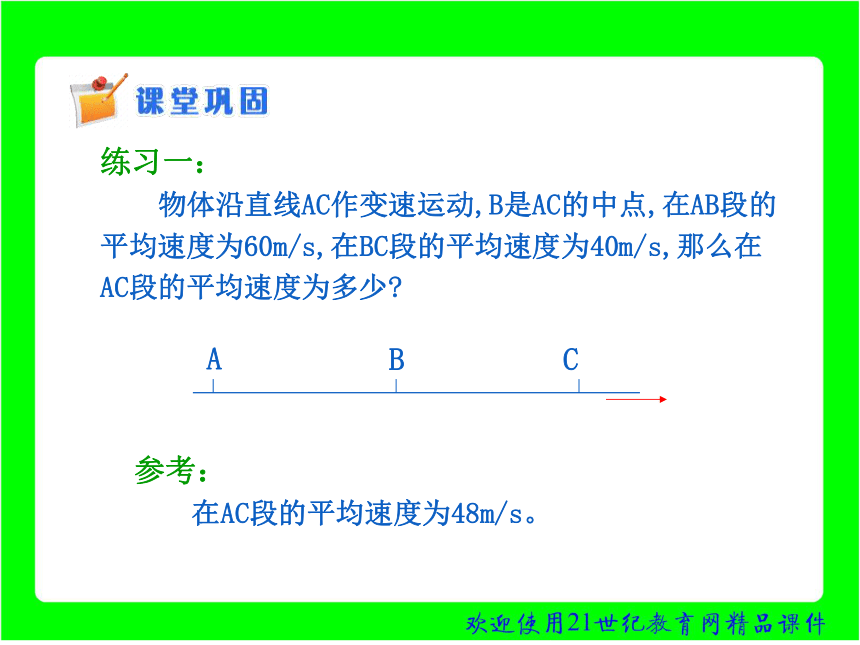
练习一： 物体沿直线AC作变速运动,B是AC的中点,在AB段的平均速度为60m/s,在BC段的平均速度为40m/s,那么在AC段的平均速度为多少
A
C
B
参考： 在AC段的平均速度为48m/s。
练习二： 一辆汽车沿笔直的公路行驶，第1ｓ内通过5ｍ的距离，第2ｓ内和第3ｓ内各通过20ｍ的距离，第4ｓ内又通过15ｍ的距离.求汽车在最初两秒内的平均速度和这4ｓ内的平均速度各是多少
参考：根据平均速度的定义式得：
=12.5m/s
υ1=
-
υ2=
-
X1 + X2
t1 + t2
m/s
=
5+20
1+1
X1+X2+X3+X4
t
=
5+20+20+15
4
m/s
=15m/s
三、平均速度和瞬时速度
(2)瞬时速度
三、平均速度和瞬时速度
(2)瞬时速度
由于υ=△x/△t，若△t越小，则描述越精确；想象△t非常小时，可以认为此时的平均速度△x/△t就是瞬时速度。
定义： 运动物体经过某一时刻(或某一位置)的速度。
瞬时速度能对变速运动做精确描述。
瞬时速度是矢量，方向是轨迹上物体所在点的切线方向（与轨迹在该点的延伸方向一致）。
练习： (1)试判断下面的几个速度中哪个是平均速度？哪个是瞬时速度？ A.子弹出枪口的速度是800m/s，以790m/s的速度击中目标。 B.汽车从甲站行驶到乙站的速度是40km/h。 C.汽车通过站牌时的速度是72km/h。 D.小球第3s末的速度是6m/s。
(2)子弹离开枪口时的 速度是900m/s；汽车启动后第5s的 速度是15m/s；小球在第4s内的 速度是5m/s；一人在百米赛跑冲过终点时的 速度是10m/s。
(3)短跑运动员在100m的竞赛中，测得他5s末的速度是8.7m/s，10s末到达终点的速度为10.3m/s，此运动员在这100m中的平均速度的大小是（ ）
　A.9.5m/s 　B.10.3m/s 　C.9m/s D.10m/s
四、速度和速率
(1)速率
瞬时速度的大小叫瞬时速率，简称速率。
汽车速度计显示的速度可以看作瞬时速度，瞬时速度的大小（80Km/h）即为速率。
四、速度和速率
(2)速率与速度的区别
速度是矢量，既有大小又有方向。速率只表示瞬时速度的大小，不能表示它的方向。
如：汽车速度计不能显示车辆运动的方向，它只能显示汽车在运行过程中的瞬时速度的大小。日常生活与物理学中说到的“速度”，有时是指速率，应根据具体情况进行判断。
(3) 常见物体的速度
在变速直线运动s-t图象中,某段时间内的平均速度,可用图象在该段时间内的割线的斜率k来表示，如图所示。
在变速直线运动s-t图象中，某时刻的瞬时速度，可用图象上过该时刻（或该位置）对应点的切线斜率k来表示，如图所示。