动能定理习题课

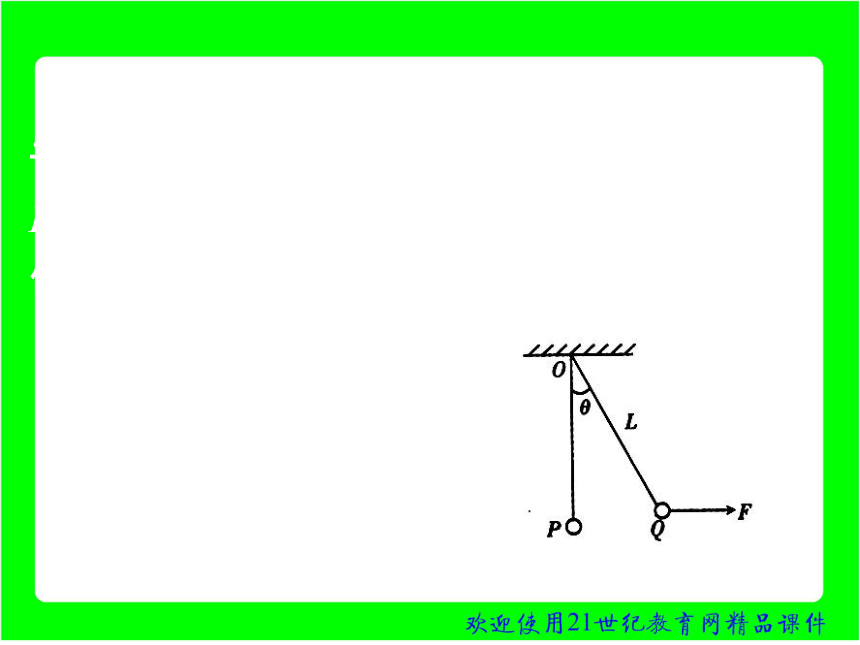
课件10张PPT。动能定理习题课2. 文字表述：合力在一个过程中对物体所做的功等于物体动能的变化.1. 公式：W合 = Ek2?Ek1= ΔEk =动 能 定 理3. 对动能定理的理解 (1)动能定理的计算式为标量式，v为相对地面的速率。W为合力的功。 (2)可用于求功、力、质量、位移、初速度、末速度等物理量。 1.一质量为m的小球，用长为L的轻绳悬挂
于O点。小球在水平拉力F作用下，从平衡位置
P点很缓慢地移动到Q点，如图所示，则力F所
做的功为（ ） A. mgLcos? B. mgL（1-cos?） C. FLcos? D. FL? 2.竖直放置的轻弹簧下
端固定在地面上，上端与轻
质平板相连，平板与地面间
的距离为H1，如图所示，现
将一质量为m的物体轻轻放在
平板中心，让它由静止开始向下运动，直至物
块速度为零，此时平板与地面间的距离为H2，若取弹簧无形变时为弹性势能的零点，则此时弹簧的弹性势能为____________。 3.一辆汽车在平直的公路上以速度v0开始
加速行驶，经过一段时间t，前进了距离s，此
时恰好达到其最大速度vmax。设此过程中汽车
发动机始终以额定功率P工作，汽车所受的阻
力恒为F，则在这段时间里，发动机所做的功
为（ ） 1. 动能定理不但能处理恒力做功的问题，对变力做功同样适用。 2. 动能定理不但适用直线运动，也适用于曲线运动。 3. 较牛顿定律处理问题更具优越性，广泛应用于解决各种力学问题。应用动能定理求变力的功归纳一 4. 物体从高出地面H处由静止自由落
下，不考虑空气阻力，落至地面进入沙坑h
处时停止（如图所示），求物体在沙坑中受
到的平均阻力是其重力的多少倍。多过程问题归纳二 若物体在某个运动过程中包含有几个不同的小过程，此时可以分段考虑，也可以对全过程考虑，但如能对整个过程利用动能定理列式则往往能使问题简化。 5. 如图，AB为
1/4圆弧轨道，BC为水
平直轨道，圆弧的半径
为R，BC的长度也为R。一质量为m的物体，
与两个轨道与物体的动摩擦因素都为?，当
它由轨道顶端A从静止开始下落，恰好运动到C处停止，那么物体在AB段克服摩擦力所做的功为（ ）