太阳与行星间的引力
图片预览







文档简介
课件24张PPT。太阳与行星间的引力1. 问题的提出:
开普勒找出行
星运动规律后,人
们开始更深入的思
考:为什么行星围
绕太阳运动?一、行星的运动2. 猜想与假设1. 伽利略: 一切物体都有合并的趋势,这
种趋势导致物体做圆周运动。
2. 开普勒: 受到了来自太阳的类似与磁力 的作用。
3. 笛卡儿: 在行星周围有旋转的物质(以太) 作用在行星上,使得行星绕太阳运动。4. 胡克、哈雷等: 受到了太阳对它的引 力,证明了如果行星的轨道是圆形的, 其所受的引力大小跟行星到太阳的距离 的二次方成反比,但没法证明在椭圆轨 道规律也成立。
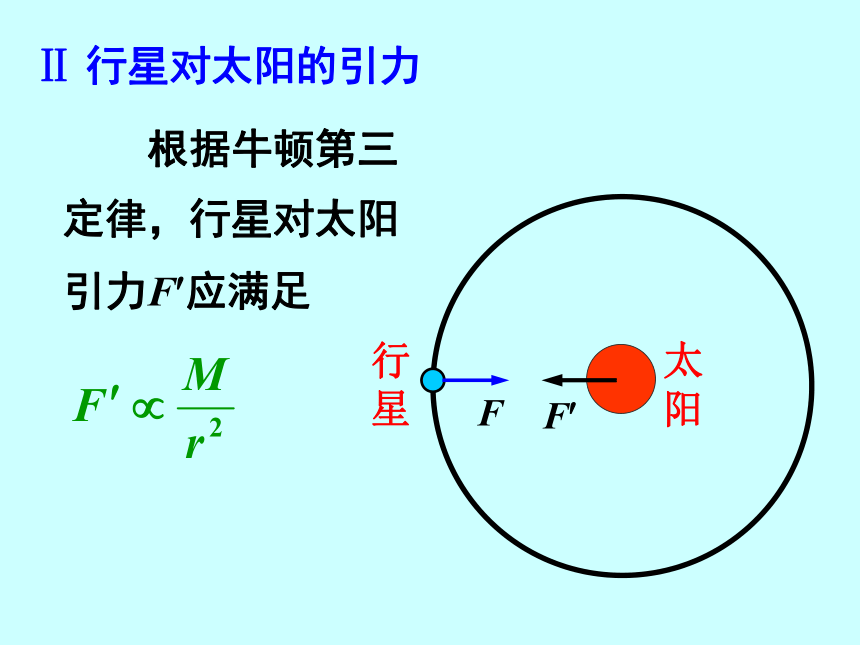
5. 牛顿: 如果太阳和行星间的引力与距离 的二次方成反比,则行星的轨迹是椭 圆。并且阐述了普遍意义下的万有引力 定律。行星太阳3. 简化模型4. 追寻牛顿的足迹——演绎与推理Ⅰ太阳对行星的引力 1. 设行星的质量为m,速度为v, 行星到太阳的距离为r,则行星绕太阳 做匀速圆周运动的向心力太阳对行星 的引力来提供:4. 追寻牛顿的足迹——演绎与推理Ⅰ太阳对行星的引力即: 太阳对不同行星的引力,与行星的 质量成正比,与行星和太阳间的距离的 二次方成反比。 根据牛顿第三 定律,行星对太阳 引力F?应满足Ⅱ 行星对太阳的引力概括起来有Ⅲ 太阳与行星间的引力概括起来有则太阳与行星间引力大小为Ⅲ 太阳与行星间的引力概括起来有G比例系数, 与太阳、行星的质量无关则太阳与行星间引力大小为Ⅲ 太阳与行星间的引力概括起来有G比例系数, 与太阳、行星的质量无关则太阳与行星间引力大小为方向:沿着太阳和行星的连线Ⅲ 太阳与行星间的引力 如果要验证太阳与行星间的引力规律是否适用于行星与它的卫星,我们需要观测这些卫星运动的哪些数据?观测前你对这些数据的规律有什么假设? 行星绕太阳运动遵守这个规律,那么在其他地方是否适用这个规律呢? 宇宙间的一切物体都是相互吸引的,两个物体间的引力大小与它们的质量的乘积成正比,跟它们距离的平方成反比。二、万有引力定律1.内容F=Gm1m2/r2 2. 公式: G=6.67×10-11Nm2/kg2,数值上 等于两个质量均为1kg的物体相距1米 时它们之间的相互吸引力。F=Gm1m2/r2 3.引力常量:2. 公式:4. 万有引力的适用条件:(1)适用于质点(2)当两物体是质量分布均匀的球体时, 式中r指两球心间的距离。4. 万有引力的适用条件:(3)若物体不能视为质点,则可把每一个物 体视为若干个质点的集合,然后按定律 求出各质点间的引力,再按矢量法求它 们的合力。5. 万有引力的特征: (1)普遍性: 普遍存在于宇宙中的任何有 质量的物体间的吸引力,是自然界的基本相 互作用之一.5. 万有引力的特征: (1)普遍性: 普遍存在于宇宙中的任何有 质量的物体间的吸引力,是自然界的基本相 互作用之一. (2)相互性: 两个物体相互作用的引力是 一对作用力和反作用力,符合牛顿第三定律.5. 万有引力的特征: (1)普遍性: 普遍存在于宇宙中的任何有 质量的物体间的吸引力,是自然界的基本相 互作用之一. (2)相互性: 两个物体相互作用的引力是 一对作用力和反作用力,符合牛顿第三定律. (3)宏观性: 通常情况下,万有引力非常 小,只有在质量巨大的天体间或天体与物体 间它的存在才有宏观的实际意义.5. 万有引力的特征:
2. 开普勒: 受到了来自太阳的类似与磁力 的作用。
3. 笛卡儿: 在行星周围有旋转的物质(以太) 作用在行星上,使得行星绕太阳运动。4. 胡克、哈雷等: 受到了太阳对它的引 力,证明了如果行星的轨道是圆形的, 其所受的引力大小跟行星到太阳的距离 的二次方成反比,但没法证明在椭圆轨 道规律也成立。
5. 牛顿: 如果太阳和行星间的引力与距离 的二次方成反比,则行星的轨迹是椭 圆。并且阐述了普遍意义下的万有引力 定律。行星太阳3. 简化模型4. 追寻牛顿的足迹——演绎与推理Ⅰ太阳对行星的引力 1. 设行星的质量为m,速度为v, 行星到太阳的距离为r,则行星绕太阳 做匀速圆周运动的向心力太阳对行星 的引力来提供:4. 追寻牛顿的足迹——演绎与推理Ⅰ太阳对行星的引力即: 太阳对不同行星的引力,与行星的 质量成正比,与行星和太阳间的距离的 二次方成反比。 根据牛顿第三 定律,行星对太阳 引力F?应满足Ⅱ 行星对太阳的引力概括起来有Ⅲ 太阳与行星间的引力概括起来有则太阳与行星间引力大小为Ⅲ 太阳与行星间的引力概括起来有G比例系数, 与太阳、行星的质量无关则太阳与行星间引力大小为Ⅲ 太阳与行星间的引力概括起来有G比例系数, 与太阳、行星的质量无关则太阳与行星间引力大小为方向:沿着太阳和行星的连线Ⅲ 太阳与行星间的引力 如果要验证太阳与行星间的引力规律是否适用于行星与它的卫星,我们需要观测这些卫星运动的哪些数据?观测前你对这些数据的规律有什么假设? 行星绕太阳运动遵守这个规律,那么在其他地方是否适用这个规律呢? 宇宙间的一切物体都是相互吸引的,两个物体间的引力大小与它们的质量的乘积成正比,跟它们距离的平方成反比。二、万有引力定律1.内容F=Gm1m2/r2 2. 公式: G=6.67×10-11Nm2/kg2,数值上 等于两个质量均为1kg的物体相距1米 时它们之间的相互吸引力。F=Gm1m2/r2 3.引力常量:2. 公式:4. 万有引力的适用条件:(1)适用于质点(2)当两物体是质量分布均匀的球体时, 式中r指两球心间的距离。4. 万有引力的适用条件:(3)若物体不能视为质点,则可把每一个物 体视为若干个质点的集合,然后按定律 求出各质点间的引力,再按矢量法求它 们的合力。5. 万有引力的特征: (1)普遍性: 普遍存在于宇宙中的任何有 质量的物体间的吸引力,是自然界的基本相 互作用之一.5. 万有引力的特征: (1)普遍性: 普遍存在于宇宙中的任何有 质量的物体间的吸引力,是自然界的基本相 互作用之一. (2)相互性: 两个物体相互作用的引力是 一对作用力和反作用力,符合牛顿第三定律.5. 万有引力的特征: (1)普遍性: 普遍存在于宇宙中的任何有 质量的物体间的吸引力,是自然界的基本相 互作用之一. (2)相互性: 两个物体相互作用的引力是 一对作用力和反作用力,符合牛顿第三定律. (3)宏观性: 通常情况下,万有引力非常 小,只有在质量巨大的天体间或天体与物体 间它的存在才有宏观的实际意义.5. 万有引力的特征:
