4.4 图形变化的简单运用同步练习(含答案)
文档属性
| 名称 | 4.4 图形变化的简单运用同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-08 00:00:00 | ||
图片预览


文档简介
第四章 图形的平移和旋转
4 图形变化的简单运用
自主预习
图案设计的一般过程:(1)确定设计图案表达意图;(2)分析设计图案所给定的____________;
(3)对基本图形综合运用__________变换、________变换、________变换,力求设计的图案形式清新、寓意明确。
课堂巩固
知识点:利用几何变换设计图案
1.如图,A,B,C,D四点在同一条直线上,AB=CD,AE=BF,CE=DF.则下列结论正确的是( )
A.△ACE和△BDF成轴对称
B.△ACE经过旋转可以和△BDF重合
C.△ACE和△BDF成中心对称
D.△ACE经过平移可以和△BDF重合
2.下图所示图案是由六个全等的四边形拼成的,它也可以看做是以“某个图案”为基础通过旋转得到的以下图案中,不能作为“某个图案”的是( )
3.如图,要把右边的“新月形”变为左边的“新月形”,最简便的方法是________________。
4.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠部分,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有_________种。
5.如图,试说明△A’B’C’是由△ABC通过怎样的图形变换或变换组合(平移、旋转、轴对称)得到的?
课后提升
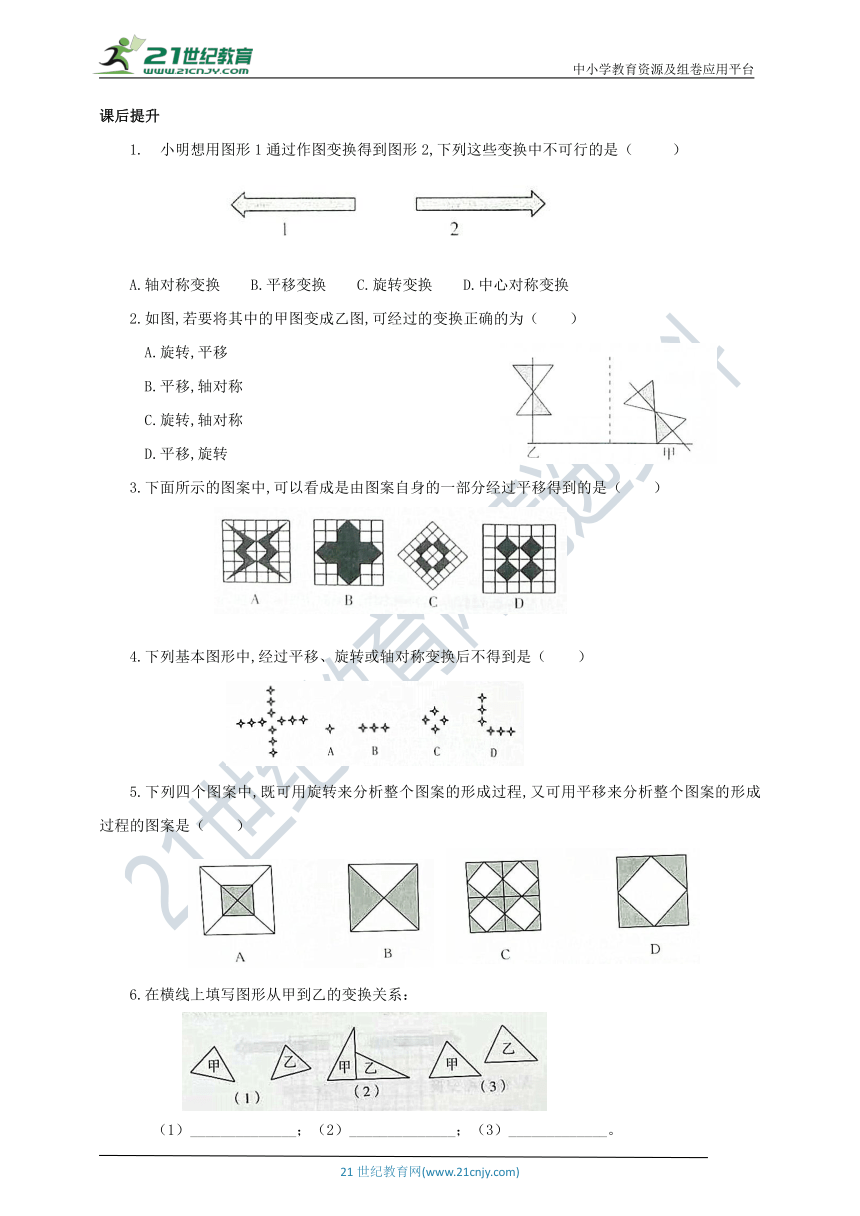
小明想用图形1通过作图变换得到图形2,下列这些变换中不可行的是( )
A.轴对称变换 B.平移变换 C.旋转变换 D.中心对称变换
2.如图,若要将其中的甲图变成乙图,可经过的变换正确的为( )
A.旋转,平移
B.平移,轴对称
C.旋转,轴对称
D.平移,旋转
3.下面所示的图案中,可以看成是由图案自身的一部分经过平移得到的是( )
4.下列基本图形中,经过平移、旋转或轴对称变换后不得到是( )
5.下列四个图案中,既可用旋转来分析整个图案的形成过程,又可用平移来分析整个图案的形成过程的图案是( )
6.在横线上填写图形从甲到乙的变换关系:
(1)______________;(2)______________;(3)_____________。
7.在如图4×21的方格纸中,右侧的四个三角形中,不能由△ABC经过旋转或平移得到的是_______________。(填写序号即可)
8.如图,8×8方格纸上的两条对称轴EF,MN相交于中心点O,将格点△ABC(顶点在小正方形的顶点上)分别做下列三种变换:①先以点A为旋转中顺时针旋转90°,再向右平移4格,最后向上平移4格;②先以点O为对称中心作中心对称图形,再以点A的对应点为中心逆时针旋转90°;③先以直线MN为轴对称作轴对称图形,再向上平移4格,最后以点A的对应点为旋转中心顺时针旋转90°,其中能将△ABC变换成△PQR的是______________。(填写序号即可)
9.如图,在6×6的方格中,点A,O,B都在小方格的顶点上,请在方格中取点C和点D,画△AOC和
△BOD,使这两个三角形全等。
(1)在图1中画出的两个三角形,可以使其中一个三角形通过轴对称得到另一个三角形;
(2)在图2中画出的两个三角形,可以使其中一个三角形通过旋转得到另一个三角形.
素养锤炼
在网格中画对称图形
(1)如图是五个小正方形拼成的图形,请你移动其中个小正方形,重新拼成一个图形,使得所拼成的形满足下列条件,并分别画在图①、图②、图③中(只需各画一个,内部涂上阴影);
①是轴对称图形,但不是中心对称图形;
②是中心对称图形,但不是轴对称图形;
③既是轴对称图形,又是中心对称图形。
(2)请你在图④的网格内设计一个商标,满足下列要求:
①是顶点在格点的凸多边形(不是平行四边形);
②是中心对称图形,但不是轴对称图形;
③商标内部涂上阴影。
参考答案及解析
自主预习
基本图形 平移 旋转 轴对称
课堂巩固
1.D 2.B
3.以图中直线为对称轴,作右边图形的对称图形 4. 4
5.解:通过旋转、平移得到.以点B为旋转中心,逆时针旋90°,向下平移1个单位,再向右平移5个单位.
课后提升
1.B 2.C 3.D 4.C 5.C
6.(1)轴对称 (2)旋转 (3)平移 7.② 8.①②③
9.解: (1)如图1所示:△ACO,△DOB即为所求;
(2)如图2所示:△ACO,△DOB即为所求。
素养锤炼
解:(1)如图①,是轴对称图形,但不是中心对称图形;
如图②,是中心对称图形,但不是轴对称图形;
如图③,既是轴对称图形,又是中心对称图形。
(2)如图④即为所求。
4 图形变化的简单运用
自主预习
图案设计的一般过程:(1)确定设计图案表达意图;(2)分析设计图案所给定的____________;
(3)对基本图形综合运用__________变换、________变换、________变换,力求设计的图案形式清新、寓意明确。
课堂巩固
知识点:利用几何变换设计图案
1.如图,A,B,C,D四点在同一条直线上,AB=CD,AE=BF,CE=DF.则下列结论正确的是( )
A.△ACE和△BDF成轴对称
B.△ACE经过旋转可以和△BDF重合
C.△ACE和△BDF成中心对称
D.△ACE经过平移可以和△BDF重合
2.下图所示图案是由六个全等的四边形拼成的,它也可以看做是以“某个图案”为基础通过旋转得到的以下图案中,不能作为“某个图案”的是( )
3.如图,要把右边的“新月形”变为左边的“新月形”,最简便的方法是________________。
4.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠部分,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有_________种。
5.如图,试说明△A’B’C’是由△ABC通过怎样的图形变换或变换组合(平移、旋转、轴对称)得到的?
课后提升
小明想用图形1通过作图变换得到图形2,下列这些变换中不可行的是( )
A.轴对称变换 B.平移变换 C.旋转变换 D.中心对称变换
2.如图,若要将其中的甲图变成乙图,可经过的变换正确的为( )
A.旋转,平移
B.平移,轴对称
C.旋转,轴对称
D.平移,旋转
3.下面所示的图案中,可以看成是由图案自身的一部分经过平移得到的是( )
4.下列基本图形中,经过平移、旋转或轴对称变换后不得到是( )
5.下列四个图案中,既可用旋转来分析整个图案的形成过程,又可用平移来分析整个图案的形成过程的图案是( )
6.在横线上填写图形从甲到乙的变换关系:
(1)______________;(2)______________;(3)_____________。
7.在如图4×21的方格纸中,右侧的四个三角形中,不能由△ABC经过旋转或平移得到的是_______________。(填写序号即可)
8.如图,8×8方格纸上的两条对称轴EF,MN相交于中心点O,将格点△ABC(顶点在小正方形的顶点上)分别做下列三种变换:①先以点A为旋转中顺时针旋转90°,再向右平移4格,最后向上平移4格;②先以点O为对称中心作中心对称图形,再以点A的对应点为中心逆时针旋转90°;③先以直线MN为轴对称作轴对称图形,再向上平移4格,最后以点A的对应点为旋转中心顺时针旋转90°,其中能将△ABC变换成△PQR的是______________。(填写序号即可)
9.如图,在6×6的方格中,点A,O,B都在小方格的顶点上,请在方格中取点C和点D,画△AOC和
△BOD,使这两个三角形全等。
(1)在图1中画出的两个三角形,可以使其中一个三角形通过轴对称得到另一个三角形;
(2)在图2中画出的两个三角形,可以使其中一个三角形通过旋转得到另一个三角形.
素养锤炼
在网格中画对称图形
(1)如图是五个小正方形拼成的图形,请你移动其中个小正方形,重新拼成一个图形,使得所拼成的形满足下列条件,并分别画在图①、图②、图③中(只需各画一个,内部涂上阴影);
①是轴对称图形,但不是中心对称图形;
②是中心对称图形,但不是轴对称图形;
③既是轴对称图形,又是中心对称图形。
(2)请你在图④的网格内设计一个商标,满足下列要求:
①是顶点在格点的凸多边形(不是平行四边形);
②是中心对称图形,但不是轴对称图形;
③商标内部涂上阴影。
参考答案及解析
自主预习
基本图形 平移 旋转 轴对称
课堂巩固
1.D 2.B
3.以图中直线为对称轴,作右边图形的对称图形 4. 4
5.解:通过旋转、平移得到.以点B为旋转中心,逆时针旋90°,向下平移1个单位,再向右平移5个单位.
课后提升
1.B 2.C 3.D 4.C 5.C
6.(1)轴对称 (2)旋转 (3)平移 7.② 8.①②③
9.解: (1)如图1所示:△ACO,△DOB即为所求;
(2)如图2所示:△ACO,△DOB即为所求。
素养锤炼
解:(1)如图①,是轴对称图形,但不是中心对称图形;
如图②,是中心对称图形,但不是轴对称图形;
如图③,既是轴对称图形,又是中心对称图形。
(2)如图④即为所求。
