第四章 图形的平移与旋转单元测试题(含答案)
文档属性
| 名称 | 第四章 图形的平移与旋转单元测试题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-09 00:00:00 | ||
图片预览


文档简介
周测三
时间:45分钟 满分:100分
一、精心选一选(每题3分,共24分)
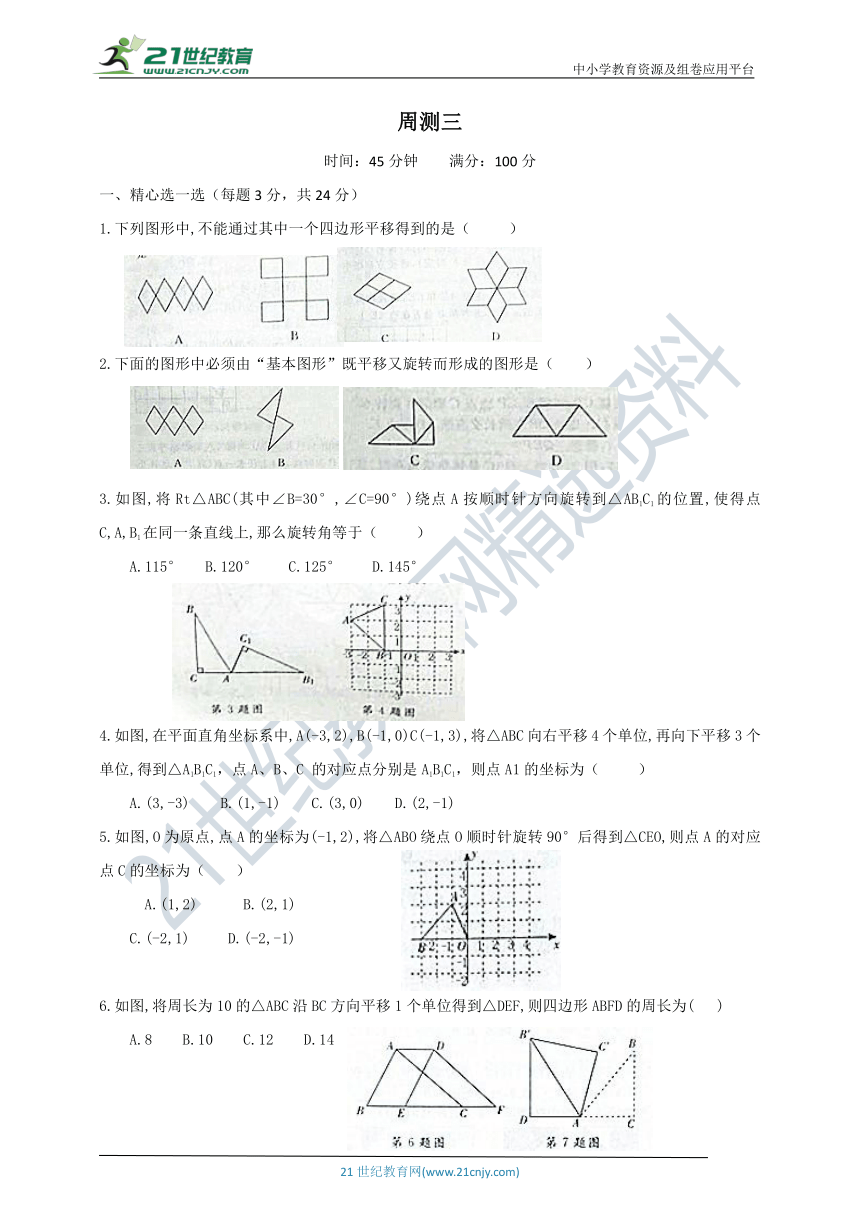
1.下列图形中,不能通过其中一个四边形平移得到的是( )
2.下面的图形中必须由“基本图形”既平移又旋转而形成的图形是( )
3.如图,将Rt△ABC(其中∠B=30°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角等于( )
A.115° B.120° C.125° D.145°
4.如图,在平面直角坐标系中,A(-3,2),B(-1,0)C(-1,3),将△ABC向右平移4个单位,再向下平移3个单位,得到△A1B1C1,点A、B、C 的对应点分别是A1B1C1,则点A1的坐标为( )
A.(3,-3) B.(1,-1) C.(3,0) D.(2,-1)
5.如图,O为原点,点A的坐标为(-1,2),将△ABO绕点O顺时针旋转90°后得到△CEO,则点A的对应点C的坐标为( )
A.(1,2) B.(2,1)
C.(-2,1) D.(-2,-1)
6.如图,将周长为10的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
A.8 B.10 C.12 D.14
7.如图,△ABC为等腰直角三角形,∠ACB=90°,将△ABC绕点A逆时针旋转75°,得到△AB’C’,过点B’作B’D⊥CA,交CA的延长线于点D,若AC=6,则AD的长为( )
A.2 B.3 C. D.
8.如图,△ABC是等腰直角三角形,DE是过点C的直线,BD⊥DE,AE⊥DE,则△BDC与△ACE通过下列变换:①绕点C旋转后重合;
②沿AB的中垂线翻折后重合;
③沿ED方向平移△CEA后与△BDC重合;
④绕中点M逆时针旋转90度,则△ACE与△BDC重合;
⑤先沿ED方向平移△CEA,使点E与点D重合后,再将平移后的三角形绕点D逆时针旋转90度,则△BDC与△ACE重合。
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、细心填一填(每题4分,共24分)
9.一个图形无论经过平移变换还是旋转变换,下列结论一定正确的是__________(把所有你认为正确的序号都写上)。
①对应线段平行;②对应线段相等;③对应角相等;④图形的形状和大小都不变。
10.如图,将△ABC平移到△A’B’C’的位置(点B’在AC边上),若∠B=55°,∠C=100°,则∠AB’A’的度数为___________。
11.如图,在一块长为12cm,宽为6cm的矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是2cm),则空白部分表示的草地面积______________。
12.在平面直角坐标系中,已知线段AB的两个端点的坐标分别是A(-4,-1),B(1,1),将线段AB平移后得到线段A'B'(点A的对应点为点A’),若点A’的坐标为(-2,a),则点B'的坐标为(b,4),则=_________。
13.如图所示,将图形(1)以点O为旋转中心,每次旋转90°,则第2015次旋转后的图形是__________(在下列各图中选填正确图形的序号即可)。
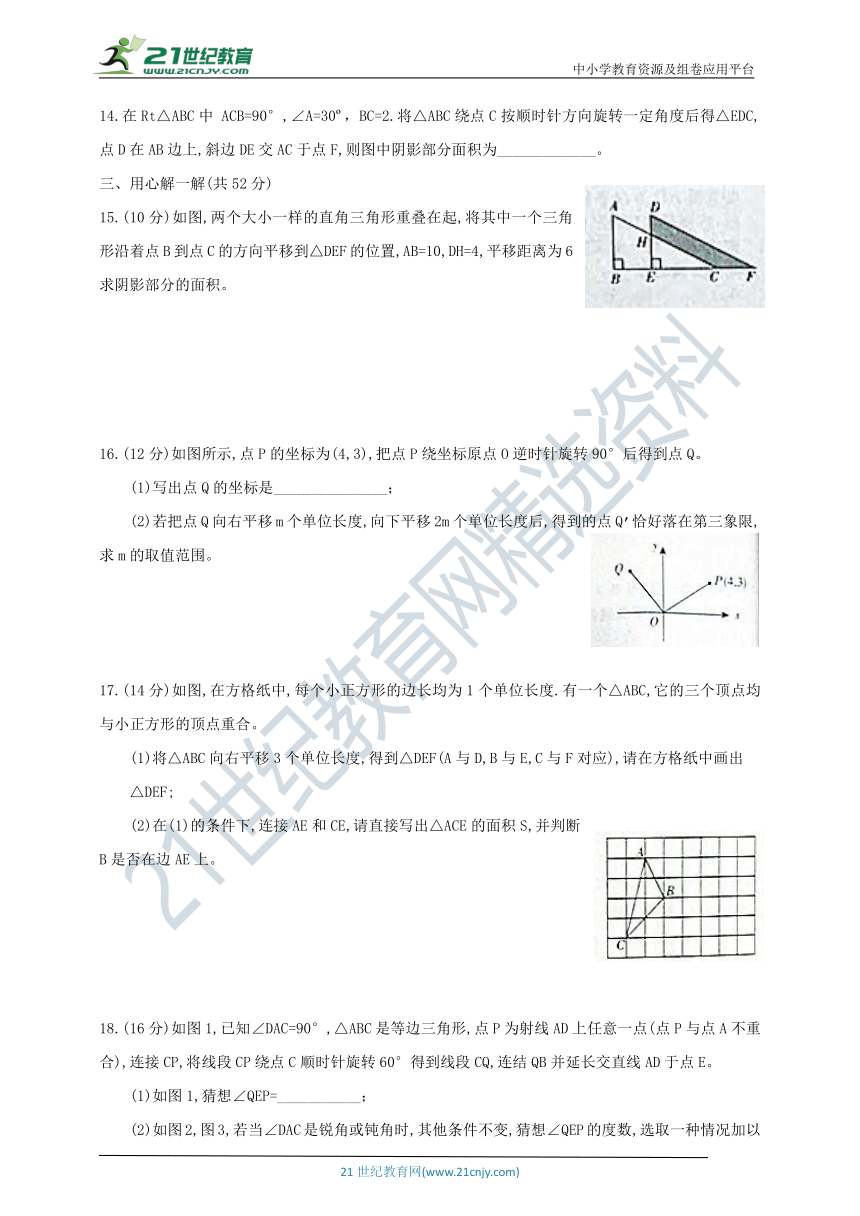
14.在Rt△ABC中 ACB=90°,∠A=30o,BC=2.将△ABC绕点C按顺时针方向旋转一定角度后得△EDC,点D在AB边上,斜边DE交AC于点F,则图中阴影部分面积为_____________。
三、用心解一解(共52分)
15.(10分)如图,两个大小一样的直角三角形重叠在起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=10,DH=4,平移距离为6,求阴影部分的面积。
16.(12分)如图所示,点P的坐标为(4,3),把点P绕坐标原点O逆时针旋转90°后得到点Q。
(1)写出点Q的坐标是_______________;
(2)若把点Q向右平移m个单位长度,向下平移2m个单位长度后,得到的点Q’恰好落在第三象限,求m的取值范围。
17.(14分)如图,在方格纸中,每个小正方形的边长均为1个单位长度.有一个△ABC,它的三个顶点均与小正方形的顶点重合。
(1)将△ABC向右平移3个单位长度,得到△DEF(A与D,B与E,C与F对应),请在方格纸中画出
△DEF;
(2)在(1)的条件下,连接AE和CE,请直接写出△ACE的面积S,并判断B是否在边AE上。
18.(16分)如图1,已知∠DAC=90°,△ABC是等边三角形,点P为射线AD上任意一点(点P与点A不重合),连接CP,将线段CP绕点C顺时针旋转60°得到线段CQ,连结QB并延长交直线AD于点E。
(1)如图1,猜想∠QEP=___________;
(2)如图2,图3,若当∠DAC是锐角或钝角时,其他条件不变,猜想∠QEP的度数,选取一种情况加以证明。
参考答案及解析
1.D 2.D 3.B 4.B 5.B 6.C 7.D 8.B 9.②③④
10.25 11.60cm2 12.8 13.(4) 14
15.解:∵两个三角形大小一样,
∴阴影部分面积等于梯形ABEH的面积,由平移的性质得,DE=AB,BE=6,
∵AB=10,DH=4, ∴HE=DE-DH=10-4=6,
∴阴影部分的面积=×(6+10)×6=48
16.解:(1)(-3,4);
(2)把点Q(-3,4)向右平移m个单位长度,向下平移2m个单位长度后,得到的点Q’的坐标为(-3+m,4-2m),而Q’在第三象限, 所以 解得2即m的取值范围为217.解:(1)如图所示:
(2)由图可知,S=5×4-×4×1-×2×4-×2×5=20-2-4-5=9
根据图形可知,点B不在边AE上
18.解:(1)∠QEP=60°;
证明:连接PQ。∵PC=CQ,且∠PCQ=60°,则△CQB和△CPA中,PC=CQ;∠PCQ=∠ACB; AC=BC
∴△CQB≌△CPA(SAS), ∴∠CQB=∠CPA,
又因为在△PEM和△CQM中,∠EMP=∠CMQ,∴∠QEP=∠QCP=60°
故答案为:60;
(2)∠QEP=60°.以∠DAC是锐角为例
证明:如图2
∵△ABC是等边三角形, ∴AC=BC,∠ACB=60°,
∵线段CP绕点C顺时针旋转60°得到线段CQ, ∴CP=CQ,∠PCQ=60°,
∴∠ACB+∠BCP=∠BCP+∠PCQ,即∠ACP=∠BCQ,在△ACP和△BCQ中: CA=CB,
∠ACP=∠BCQ, CP=CQ,
∴△ACP≌△BCQ(SAS),∴∠APC=∠Q,∠1=∠2,
∴∠QEP=∠PCQ=60o。
时间:45分钟 满分:100分
一、精心选一选(每题3分,共24分)
1.下列图形中,不能通过其中一个四边形平移得到的是( )
2.下面的图形中必须由“基本图形”既平移又旋转而形成的图形是( )
3.如图,将Rt△ABC(其中∠B=30°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角等于( )
A.115° B.120° C.125° D.145°
4.如图,在平面直角坐标系中,A(-3,2),B(-1,0)C(-1,3),将△ABC向右平移4个单位,再向下平移3个单位,得到△A1B1C1,点A、B、C 的对应点分别是A1B1C1,则点A1的坐标为( )
A.(3,-3) B.(1,-1) C.(3,0) D.(2,-1)
5.如图,O为原点,点A的坐标为(-1,2),将△ABO绕点O顺时针旋转90°后得到△CEO,则点A的对应点C的坐标为( )
A.(1,2) B.(2,1)
C.(-2,1) D.(-2,-1)
6.如图,将周长为10的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
A.8 B.10 C.12 D.14
7.如图,△ABC为等腰直角三角形,∠ACB=90°,将△ABC绕点A逆时针旋转75°,得到△AB’C’,过点B’作B’D⊥CA,交CA的延长线于点D,若AC=6,则AD的长为( )
A.2 B.3 C. D.
8.如图,△ABC是等腰直角三角形,DE是过点C的直线,BD⊥DE,AE⊥DE,则△BDC与△ACE通过下列变换:①绕点C旋转后重合;
②沿AB的中垂线翻折后重合;
③沿ED方向平移△CEA后与△BDC重合;
④绕中点M逆时针旋转90度,则△ACE与△BDC重合;
⑤先沿ED方向平移△CEA,使点E与点D重合后,再将平移后的三角形绕点D逆时针旋转90度,则△BDC与△ACE重合。
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、细心填一填(每题4分,共24分)
9.一个图形无论经过平移变换还是旋转变换,下列结论一定正确的是__________(把所有你认为正确的序号都写上)。
①对应线段平行;②对应线段相等;③对应角相等;④图形的形状和大小都不变。
10.如图,将△ABC平移到△A’B’C’的位置(点B’在AC边上),若∠B=55°,∠C=100°,则∠AB’A’的度数为___________。
11.如图,在一块长为12cm,宽为6cm的矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是2cm),则空白部分表示的草地面积______________。
12.在平面直角坐标系中,已知线段AB的两个端点的坐标分别是A(-4,-1),B(1,1),将线段AB平移后得到线段A'B'(点A的对应点为点A’),若点A’的坐标为(-2,a),则点B'的坐标为(b,4),则=_________。
13.如图所示,将图形(1)以点O为旋转中心,每次旋转90°,则第2015次旋转后的图形是__________(在下列各图中选填正确图形的序号即可)。
14.在Rt△ABC中 ACB=90°,∠A=30o,BC=2.将△ABC绕点C按顺时针方向旋转一定角度后得△EDC,点D在AB边上,斜边DE交AC于点F,则图中阴影部分面积为_____________。
三、用心解一解(共52分)
15.(10分)如图,两个大小一样的直角三角形重叠在起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=10,DH=4,平移距离为6,求阴影部分的面积。
16.(12分)如图所示,点P的坐标为(4,3),把点P绕坐标原点O逆时针旋转90°后得到点Q。
(1)写出点Q的坐标是_______________;
(2)若把点Q向右平移m个单位长度,向下平移2m个单位长度后,得到的点Q’恰好落在第三象限,求m的取值范围。
17.(14分)如图,在方格纸中,每个小正方形的边长均为1个单位长度.有一个△ABC,它的三个顶点均与小正方形的顶点重合。
(1)将△ABC向右平移3个单位长度,得到△DEF(A与D,B与E,C与F对应),请在方格纸中画出
△DEF;
(2)在(1)的条件下,连接AE和CE,请直接写出△ACE的面积S,并判断B是否在边AE上。
18.(16分)如图1,已知∠DAC=90°,△ABC是等边三角形,点P为射线AD上任意一点(点P与点A不重合),连接CP,将线段CP绕点C顺时针旋转60°得到线段CQ,连结QB并延长交直线AD于点E。
(1)如图1,猜想∠QEP=___________;
(2)如图2,图3,若当∠DAC是锐角或钝角时,其他条件不变,猜想∠QEP的度数,选取一种情况加以证明。
参考答案及解析
1.D 2.D 3.B 4.B 5.B 6.C 7.D 8.B 9.②③④
10.25 11.60cm2 12.8 13.(4) 14
15.解:∵两个三角形大小一样,
∴阴影部分面积等于梯形ABEH的面积,由平移的性质得,DE=AB,BE=6,
∵AB=10,DH=4, ∴HE=DE-DH=10-4=6,
∴阴影部分的面积=×(6+10)×6=48
16.解:(1)(-3,4);
(2)把点Q(-3,4)向右平移m个单位长度,向下平移2m个单位长度后,得到的点Q’的坐标为(-3+m,4-2m),而Q’在第三象限, 所以 解得2
(2)由图可知,S=5×4-×4×1-×2×4-×2×5=20-2-4-5=9
根据图形可知,点B不在边AE上
18.解:(1)∠QEP=60°;
证明:连接PQ。∵PC=CQ,且∠PCQ=60°,则△CQB和△CPA中,PC=CQ;∠PCQ=∠ACB; AC=BC
∴△CQB≌△CPA(SAS), ∴∠CQB=∠CPA,
又因为在△PEM和△CQM中,∠EMP=∠CMQ,∴∠QEP=∠QCP=60°
故答案为:60;
(2)∠QEP=60°.以∠DAC是锐角为例
证明:如图2
∵△ABC是等边三角形, ∴AC=BC,∠ACB=60°,
∵线段CP绕点C顺时针旋转60°得到线段CQ, ∴CP=CQ,∠PCQ=60°,
∴∠ACB+∠BCP=∠BCP+∠PCQ,即∠ACP=∠BCQ,在△ACP和△BCQ中: CA=CB,
∠ACP=∠BCQ, CP=CQ,
∴△ACP≌△BCQ(SAS),∴∠APC=∠Q,∠1=∠2,
∴∠QEP=∠PCQ=60o。
