4.3.1 中心对称同步练习(含答案)
图片预览
文档简介
第四章 图形的平移和旋转
3 中心对称
第1课时
自主预习
1.中心对称的概念:在平面内,如果把一个图形绕某个点旋转___________后,能与另一个图形______________,那么就说这两个图形关于这个点成中心对称,这个点叫做_____________,两个图形上能重合的两个点叫做_______________。
2.中心对称的性质:成中心对称的两个图形中,对应点的连线经过______________,且被__________平分。
课堂巩固
知识点一:成中心对称的定义
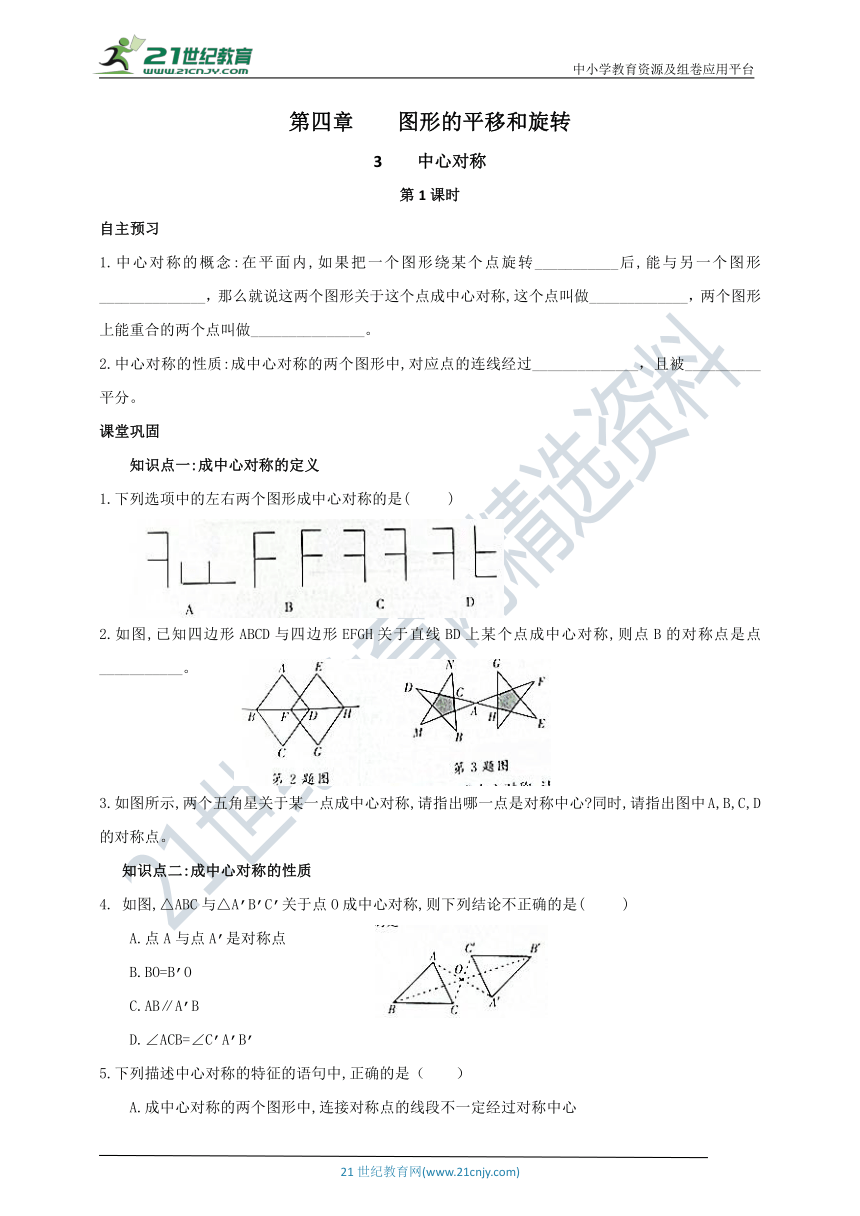
1.下列选项中的左右两个图形成中心对称的是( )
2.如图,已知四边形ABCD与四边形EFGH关于直线BD上某个点成中心对称,则点B的对称点是点___________。
3.如图所示,两个五角星关于某一点成中心对称,请指出哪一点是对称中心?同时,请指出图中A,B,C,D
的对称点。
知识点二:成中心对称的性质
如图,△ABC与△A’B’C’关于点O成中心对称,则下列结论不正确的是( )
A.点A与点A’是对称点
B.BO=B’O
C.AB∥A’B
D.∠ACB=∠C’A’B’
5.下列描述中心对称的特征的语句中,正确的是( )
A.成中心对称的两个图形中,连接对称点的线段不一定经过对称中心
B.成中心对称的两个图形中,对称中心不一定平分连接对称点的线段
C.成中心对称的两个图形中,对称点的连线一定经过对称中心,但不一定被对称中心平分
D.成中心对称的两个图形中,对称点的连线一定经过对称中心,且被对称中心平分
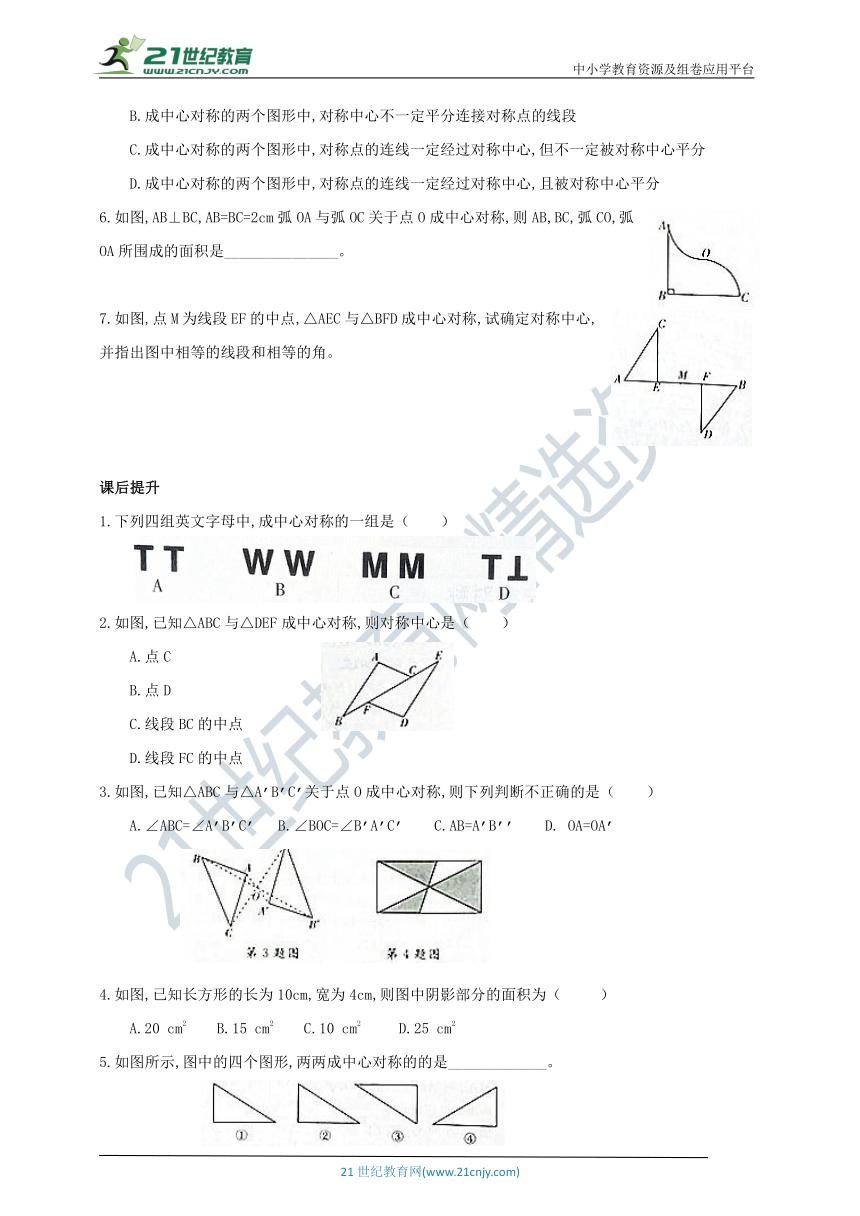
6.如图,AB⊥BC,AB=BC=2cm弧OA与弧OC关于点O成中心对称,则AB,BC,弧CO,弧OA所围成的面积是_______________。
7.如图,点M为线段EF的中点,△AEC与△BFD成中心对称,试确定对称中心,并指出图中相等的线段和相等的角。
课后提升
1.下列四组英文字母中,成中心对称的一组是( )
2.如图,已知△ABC与△DEF成中心对称,则对称中心是( )
A.点C
B.点D
C.线段BC的中点
D.线段FC的中点
3.如图,已知△ABC与△A’B’C’关于点O成中心对称,则下列判断不正确的是( )
A.∠ABC=∠A’B’C’ B.∠BOC=∠B’A’C’ C.AB=A’B’’ D. OA=OA’
4.如图,已知长方形的长为10cm,宽为4cm,则图中阴影部分的面积为( )
A.20 cm2 B.15 cm2 C.10 cm2 D.25 cm2
5.如图所示,图中的四个图形,两两成中心对称的的是_____________。
6.如图,△ABC与△A1B1C1关于点O成中心对称.若∠A=55o,∠B=90o,则∠C1的度数为_______。
7.如图,△ABC和△AB’C’成中心对称,A为对称中心若∠C=90°,
∠B=30°,BC=,则BB’的长为__________。
8.已知A,B,O三点不在同一条直线上,A与A1关于点O对称,B与B1关于点O对称,那么线段AB与A1B1的位置和数量关系是___________。
9.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,若△ABC与△A’BC’关于点B成中心对称,求AA’的长。
10.观察下图,试回答下列问题:
(1)请画出△ABC关于直线MN成轴对称的图形△A1B1C1
(2)如果点A2与点A关于某点成中心对称,请标出这个对称中心点O,并画出△ABC关于点O成中心对称的图形△A2B2C2
素养锤炼
如图,已知△ABM与△ACM关于直线AF成轴对称,△ABE与△DCE关 于点E成中心对称,点E,D,M都在线段AF上,BM的延长线交CF于点P 。
(1)求证:AC=CD;
(2)若∠BAC=2∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由。
B
参考答案及解析
自主预习
1.180° 重合 对称中心 对应点
2.对称中心 对称中心
课堂巩固
1.D 2.H
3.解:点A是对称中心;图中A,B,C,D的对称点分别是A、G、H、E 。
4.D 5.D 6. 2 cm2
7.解:观察图形可知,A,E,M,F,B共线,M为线段EF的中点。
∴对称中心为M点,
根据中心对称的性质可知,相等线段为AC=BD,CE=DF,AE=BF,EM=FM,AM=BM, AF=BE,
相等的角为:∠A=∠B,∠C=∠D,∠CEA=∠DFB,∠CEB=∠DFA
课后提升
1.D 2.D 3.B 4.A 5.①和③,②和③ 6.35° 7. 8.平行且相等
9.解:∵∠C=90°,AC=8,BC=6,∴
又∵△ABC与△A’BC’关于点B成中心对称, ∴AB=A’B=10。
∴ AA′=AB+A'B=20。
10.解:(1)如图所示,△A1B1C1即为所求;
(2)找出对称中心O,△A2B2C2即为所求。
素养锤炼
(1)证明:∵△ABM与△ACM关于直线AF成轴对称, ∴AB=AC,
又∵△ABE与△DCE关于点E成中心对称,
∴AB=CD, ∴AC=CD;
(2)解:∠F=∠MCD
理由:由(1)可得∠BAE=∠CAE=∠CDE,∠CMA=∠BMA,
∵∠BAC=2∠MPC,∠BMA=∠PMF
∴设∠MPC=a,则∠BAE=∠CAE=∠CDE=a,
设∠BMA=β,则∠PMF=∠CMA=β,
∴∠F=∠CPM-∠PMF=a-β, ∠MCD=∠CDE-∠DMC=a-β,
∴∠F=∠MCD。
3 中心对称
第1课时
自主预习
1.中心对称的概念:在平面内,如果把一个图形绕某个点旋转___________后,能与另一个图形______________,那么就说这两个图形关于这个点成中心对称,这个点叫做_____________,两个图形上能重合的两个点叫做_______________。
2.中心对称的性质:成中心对称的两个图形中,对应点的连线经过______________,且被__________平分。
课堂巩固
知识点一:成中心对称的定义
1.下列选项中的左右两个图形成中心对称的是( )
2.如图,已知四边形ABCD与四边形EFGH关于直线BD上某个点成中心对称,则点B的对称点是点___________。
3.如图所示,两个五角星关于某一点成中心对称,请指出哪一点是对称中心?同时,请指出图中A,B,C,D
的对称点。
知识点二:成中心对称的性质
如图,△ABC与△A’B’C’关于点O成中心对称,则下列结论不正确的是( )
A.点A与点A’是对称点
B.BO=B’O
C.AB∥A’B
D.∠ACB=∠C’A’B’
5.下列描述中心对称的特征的语句中,正确的是( )
A.成中心对称的两个图形中,连接对称点的线段不一定经过对称中心
B.成中心对称的两个图形中,对称中心不一定平分连接对称点的线段
C.成中心对称的两个图形中,对称点的连线一定经过对称中心,但不一定被对称中心平分
D.成中心对称的两个图形中,对称点的连线一定经过对称中心,且被对称中心平分
6.如图,AB⊥BC,AB=BC=2cm弧OA与弧OC关于点O成中心对称,则AB,BC,弧CO,弧OA所围成的面积是_______________。
7.如图,点M为线段EF的中点,△AEC与△BFD成中心对称,试确定对称中心,并指出图中相等的线段和相等的角。
课后提升
1.下列四组英文字母中,成中心对称的一组是( )
2.如图,已知△ABC与△DEF成中心对称,则对称中心是( )
A.点C
B.点D
C.线段BC的中点
D.线段FC的中点
3.如图,已知△ABC与△A’B’C’关于点O成中心对称,则下列判断不正确的是( )
A.∠ABC=∠A’B’C’ B.∠BOC=∠B’A’C’ C.AB=A’B’’ D. OA=OA’
4.如图,已知长方形的长为10cm,宽为4cm,则图中阴影部分的面积为( )
A.20 cm2 B.15 cm2 C.10 cm2 D.25 cm2
5.如图所示,图中的四个图形,两两成中心对称的的是_____________。
6.如图,△ABC与△A1B1C1关于点O成中心对称.若∠A=55o,∠B=90o,则∠C1的度数为_______。
7.如图,△ABC和△AB’C’成中心对称,A为对称中心若∠C=90°,
∠B=30°,BC=,则BB’的长为__________。
8.已知A,B,O三点不在同一条直线上,A与A1关于点O对称,B与B1关于点O对称,那么线段AB与A1B1的位置和数量关系是___________。
9.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,若△ABC与△A’BC’关于点B成中心对称,求AA’的长。
10.观察下图,试回答下列问题:
(1)请画出△ABC关于直线MN成轴对称的图形△A1B1C1
(2)如果点A2与点A关于某点成中心对称,请标出这个对称中心点O,并画出△ABC关于点O成中心对称的图形△A2B2C2
素养锤炼
如图,已知△ABM与△ACM关于直线AF成轴对称,△ABE与△DCE关 于点E成中心对称,点E,D,M都在线段AF上,BM的延长线交CF于点P 。
(1)求证:AC=CD;
(2)若∠BAC=2∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由。
B
参考答案及解析
自主预习
1.180° 重合 对称中心 对应点
2.对称中心 对称中心
课堂巩固
1.D 2.H
3.解:点A是对称中心;图中A,B,C,D的对称点分别是A、G、H、E 。
4.D 5.D 6. 2 cm2
7.解:观察图形可知,A,E,M,F,B共线,M为线段EF的中点。
∴对称中心为M点,
根据中心对称的性质可知,相等线段为AC=BD,CE=DF,AE=BF,EM=FM,AM=BM, AF=BE,
相等的角为:∠A=∠B,∠C=∠D,∠CEA=∠DFB,∠CEB=∠DFA
课后提升
1.D 2.D 3.B 4.A 5.①和③,②和③ 6.35° 7. 8.平行且相等
9.解:∵∠C=90°,AC=8,BC=6,∴
又∵△ABC与△A’BC’关于点B成中心对称, ∴AB=A’B=10。
∴ AA′=AB+A'B=20。
10.解:(1)如图所示,△A1B1C1即为所求;
(2)找出对称中心O,△A2B2C2即为所求。
素养锤炼
(1)证明:∵△ABM与△ACM关于直线AF成轴对称, ∴AB=AC,
又∵△ABE与△DCE关于点E成中心对称,
∴AB=CD, ∴AC=CD;
(2)解:∠F=∠MCD
理由:由(1)可得∠BAE=∠CAE=∠CDE,∠CMA=∠BMA,
∵∠BAC=2∠MPC,∠BMA=∠PMF
∴设∠MPC=a,则∠BAE=∠CAE=∠CDE=a,
设∠BMA=β,则∠PMF=∠CMA=β,
∴∠F=∠CPM-∠PMF=a-β, ∠MCD=∠CDE-∠DMC=a-β,
∴∠F=∠MCD。
