(公开课)必修一第二章_基本初等函数(I)_复习(14张ppt)
文档属性
| 名称 | (公开课)必修一第二章_基本初等函数(I)_复习(14张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-09 14:45:35 | ||
图片预览






文档简介
第二章 基本初等函数(Ⅰ)复习
高中数学教师欧阳文丰制作
一、目标要求
1、指数与指数函数
(1)理解有理指数幂的含义,了解实数指数幂的意义,掌握幂的运算.
(2)理解指数函数的概念和意义,探索并理解指数函数的单调性与特殊点.体会指数函数是一类重要的函数模型.
2、对数与对数函数
(1)理解对数的概念及其运算,知道用换底公式能将一般对数转化成自然对数和常用对数.
(2)初步理解对数函数的概念,体会对数函数是一类重要的函数模型,探索并了解对数函数的单调性与特殊点.
(3)知道函数y=ax与y=logax互为反函数(a>0且a≠1).
3、幂函数
通过实例,了解幂函数的概念;结合具体的幂函数的图象,了解它们的变化情况.
4、函数单调性与奇偶性的关联:同学们一起背诵!
整数指数幂
有理指数幂
无理指数幂
指数
对数
定义
运算性质
指数函数
对数函数
幂函数
定义
定义
图象与性质
图象与性质
二、知识结构和思维导图
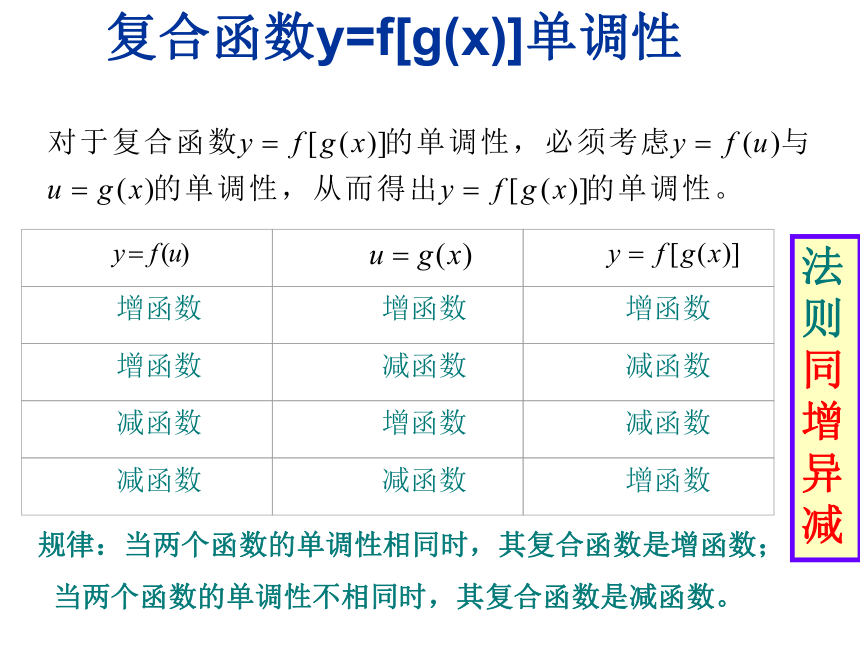
复合函数y=f[g(x)]单调性
增函数
增函数
增函数
增函数
增函数
增函数
减函数
减函数
减函数
减函数
减函数
减函数
法则同增异减
规律:当两个函数的单调性相同时,其复合函数是增函数;
当两个函数的单调性不相同时,其复合函数是减函数。
三、重点内容
(一)基本概念:
1.根式与分数指数幂:
2.对数式与指数式的转化:
3.反函数的概念
三、重点内容
(二)基本运算:
1.指数运算
2.对数运算
如果a>0,且a≠1,M>0,N>0 ,那么:
三、重点内容
(二)基本运算:
3.换底公式
三、重点内容
(三)基本性质:
R
R
当x>0时0当x<0时y>1;
当x=0时y=1;
在R上是减函数
当x>0时y>1;
当x<0时0当x=0时y=1;
在R上是增函数
01
图象
定义域
值域
性质
三、重点内容
(三)基本性质:
1
1
图象
定义域
值域
性质
三、重点内容
(三)基本性质:
四、限时练习
答案:1 、D
答案:2 、B
答案:3、D
答案:4、D
答案:5、D
四、限时练习
-2
0
x=-1
奇函数
四、限时练习
6
奇函数
五、小结
1、基本概念
2、指数式、对数式的运算
3、指数函数、对数函数、幂函数性质的应用
高中数学教师欧阳文丰制作
一、目标要求
1、指数与指数函数
(1)理解有理指数幂的含义,了解实数指数幂的意义,掌握幂的运算.
(2)理解指数函数的概念和意义,探索并理解指数函数的单调性与特殊点.体会指数函数是一类重要的函数模型.
2、对数与对数函数
(1)理解对数的概念及其运算,知道用换底公式能将一般对数转化成自然对数和常用对数.
(2)初步理解对数函数的概念,体会对数函数是一类重要的函数模型,探索并了解对数函数的单调性与特殊点.
(3)知道函数y=ax与y=logax互为反函数(a>0且a≠1).
3、幂函数
通过实例,了解幂函数的概念;结合具体的幂函数的图象,了解它们的变化情况.
4、函数单调性与奇偶性的关联:同学们一起背诵!
整数指数幂
有理指数幂
无理指数幂
指数
对数
定义
运算性质
指数函数
对数函数
幂函数
定义
定义
图象与性质
图象与性质
二、知识结构和思维导图
复合函数y=f[g(x)]单调性
增函数
增函数
增函数
增函数
增函数
增函数
减函数
减函数
减函数
减函数
减函数
减函数
法则同增异减
规律:当两个函数的单调性相同时,其复合函数是增函数;
当两个函数的单调性不相同时,其复合函数是减函数。
三、重点内容
(一)基本概念:
1.根式与分数指数幂:
2.对数式与指数式的转化:
3.反函数的概念
三、重点内容
(二)基本运算:
1.指数运算
2.对数运算
如果a>0,且a≠1,M>0,N>0 ,那么:
三、重点内容
(二)基本运算:
3.换底公式
三、重点内容
(三)基本性质:
R
R
当x>0时0
当x=0时y=1;
在R上是减函数
当x>0时y>1;
当x<0时0
在R上是增函数
0
图象
定义域
值域
性质
三、重点内容
(三)基本性质:
1
1
图象
定义域
值域
性质
三、重点内容
(三)基本性质:
四、限时练习
答案:1 、D
答案:2 、B
答案:3、D
答案:4、D
答案:5、D
四、限时练习
-2
0
x=-1
奇函数
四、限时练习
6
奇函数
五、小结
1、基本概念
2、指数式、对数式的运算
3、指数函数、对数函数、幂函数性质的应用
