人教版九年级数学上册 22.1二次函数的图象与性质复习课件46张PPT
文档属性
| 名称 | 人教版九年级数学上册 22.1二次函数的图象与性质复习课件46张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 464.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-11 14:04:33 | ||
图片预览







文档简介
第一部分 夯实基础 提分多
第三单元 函数
第13课时 二次函数的图象与性质
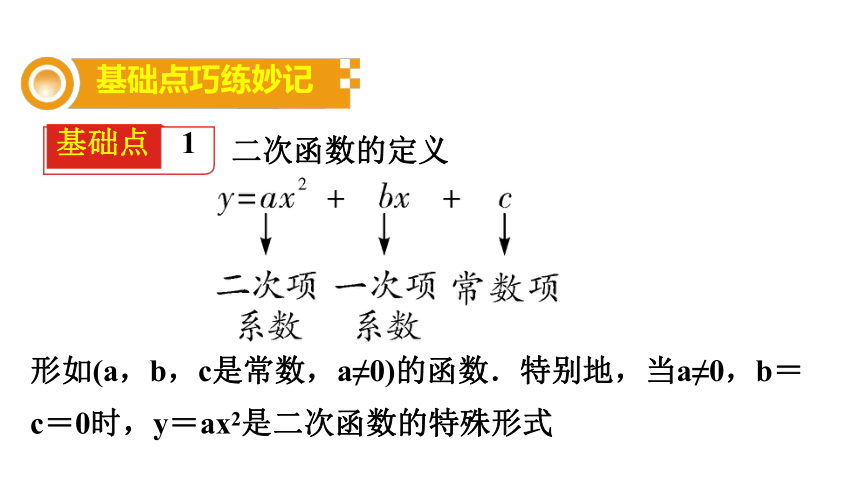
基础点 1
二次函数的定义
基础点巧练妙记
形如(a,b,c是常数,a≠0)的函数.特别地,当a≠0,b=c=0时,y=ax2是二次函数的特殊形式
基础点 2
二次函数的图象与性质
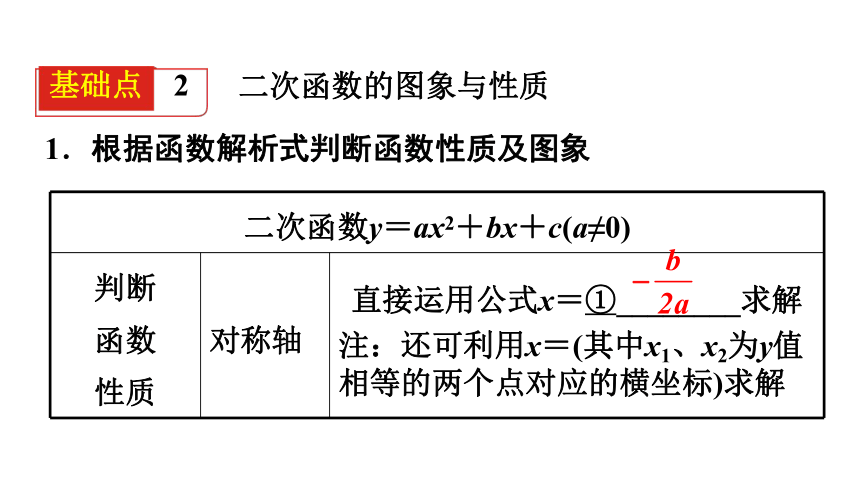
1.根据函数解析式判断函数性质及图象
二次函数y=ax2+bx+c(a≠0)
判断
函数
性质 对称轴 直接运用公式x=①________求解
注:还可利用x=(其中x1、x2为y值相等的两个点对应的横坐标)求解
二次函数y=ax2+bx+c(a≠0)
判断
函数
性质 顶点坐标 1. 直接运用顶点坐标公式
②________________求解;
2. 运用配方法将一般式转化为顶点式求解;
3. 将对称轴的x值代入函数表达式求得对应y值
二次函数y=ax2+bx+c(a≠0)
判断
函数
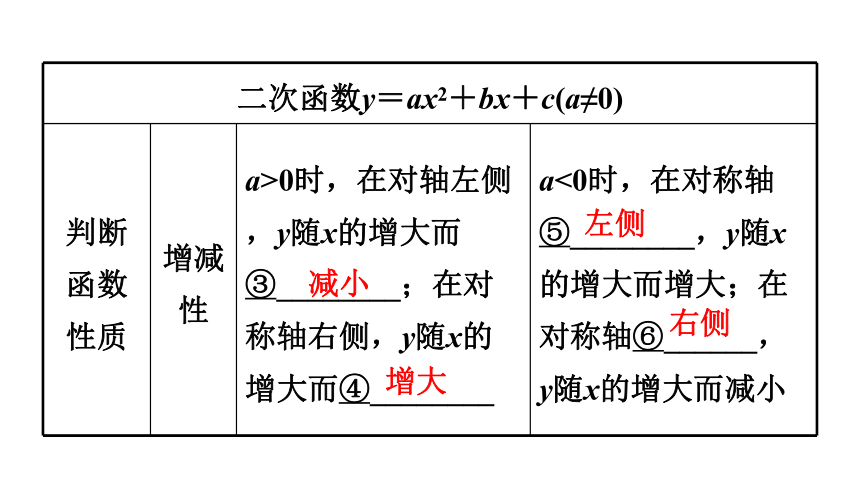
性质 增减性 a>0时,在对轴左侧,y随x的增大而③________;在对称轴右侧,y随x的增大而④________ a<0时,在对称轴⑤________,y随x的增大而增大;在对称轴⑥______,
y随x的增大而减小
减小
增大
左侧
右侧
二次函数y=ax2+bx+c(a≠0)
判断
函数
性质 最值 a>0时,当x=⑦
______时,y的最小值为 ;
离对称轴越近的点函数值越小 a<0时,y的最大值
为⑧________;
离对称轴越近的点函数值越大
二次函数y=ax2+bx+c(a≠0)
判断
函数
图象 a,决定抛物线开口方向 a⑨_____0 开口向上
a<0 开口向下
a,b决定抛物线的对称轴位置 b=0 对称轴为y轴
a、b同号 对称轴为y轴⑩____侧
a、b异号 对称轴为y轴右侧
>
左
二次函数y=ax2+bx+c(a≠0)
判断
函数
图象 c,决定抛物线与y轴交点的位置
c=0 抛物线过原点
c>0 抛物线与y轴交于?______半轴
c<0 抛物线与y轴交于?______半轴
正
负
二次函数y=ax2+bx+c(a≠0)
判断
函数
图象
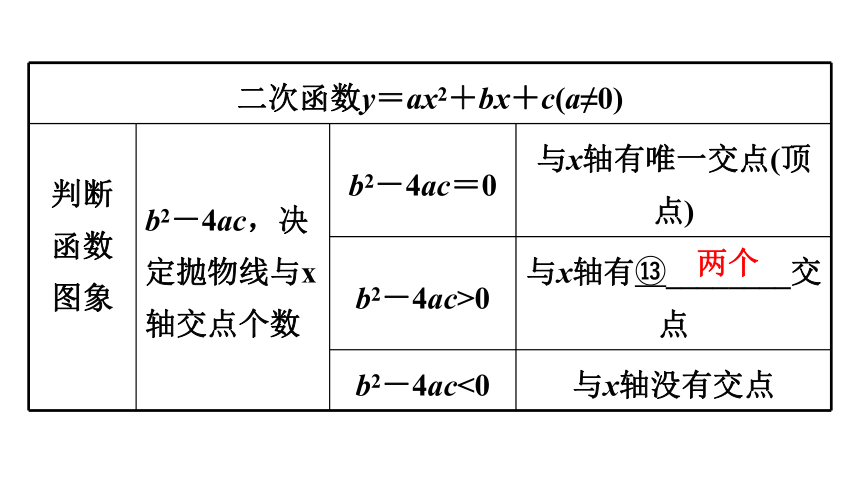
b2-4ac,决定抛物线与x轴交点个数 b2-4ac=0 与x轴有唯一交点(顶点)
b2-4ac>0 与x轴有?________交点
b2-4ac<0 与x轴没有交点
两个
二次函数y=ax2+bx+c(a≠0)
判断
特殊
关系 2a+b - 与1比较
2a-b - 与-1比较
b2-4ac 与x轴交点个数
二次函数y=ax2+bx+c(a≠0)
判断
特殊
关系 a+b+c 令x=1,看纵坐标
a-b+c 令x=-1,看纵坐标
4a+2b+c 令x=2,看纵坐标
4a-2b+c 令x=-2,看纵坐标
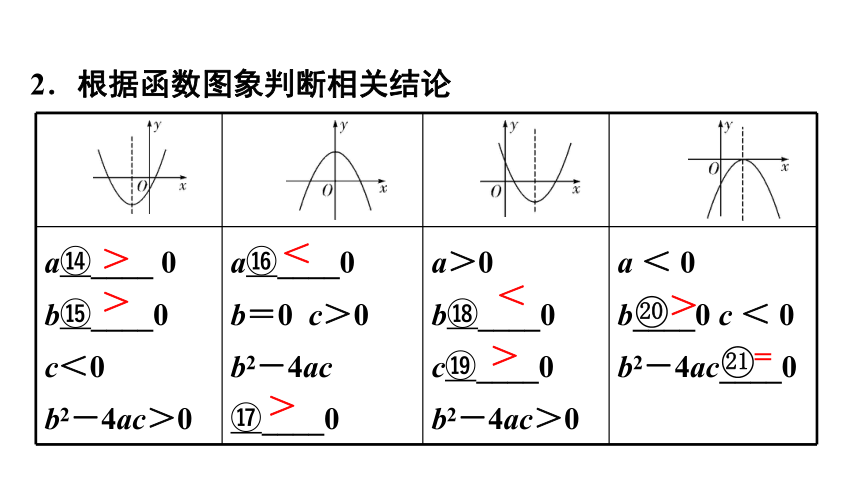
2.根据函数图象判断相关结论
a?____ 0
b?____0
c<0
b2-4ac>0 a?____0
b=0 c>0
b2-4ac
?____0 a>0
b?____0
c?____0
b2-4ac>0 a < 0
b____0 c < 0
b2-4ac____0
>
>
>
<
<
>
=
>
20
21
a>0
b?____0
c>0
b2-4ac?__0 a?____0
b>0
c?____0
b2-4ac>0 a?____0
b?____0
c=0
b2-4ac>0 a>0
b?____0
c=0
b2-4ac?__0
>
<
>
=
<
>
=
=
1.表达式的三种形式
(1)一般式:y=ax2+bx+c(a、b、c为常数,a≠0);
(2)顶点式:____________(a为常数,a≠0,(h,k)为顶点坐标);
(3)交点式:_________________ (a为常数,a≠0,x1,x2为抛物线与x轴交点的横坐标);
基础点 3
二次函数表达式的确定
y=a(x-h)2+k
y=a(x-x1)(x-x2)
顶点式 一般式 交点式,若顶点在原点,可设为y=ax2.
配方
因式分解
(4)三种表达式之间的关系
2.待定系数法求二次函数的表达式:
(1)对于二次函数y=ax2+bx+c,若系数a、b、c中有一个未知,则代入任意一点坐标;若有两个未知,则代入任意两点坐标;若三个都未知,根据下表所给的点坐标选择适当的表达式
已知 所设表达式
顶点+其他点 y=a(x-h)2+k
与x轴的两个交点+其他点 y=a(x-x1)(x-x2)
与x轴的一个交点+对称轴+其他点
任意三个点 y=ax2+bx+c
(2)联立方程(组),求得系数或常数项;将所得系数或常数项代入表达式即可.
基础点 4
二次函数图象的平移
(1)上加下减:
y=ax2+bx+c
y=ax2+bx+c+m
y=ax2+bx+c+n
向上平移m个单位
向下平移m个单位
(2)左加右减:
方法一:
y=ax2+bx+c
化为
y=a(x-h)2+k
规律:
向右平移m个单位
y=a(x-h-m)2+k
向左平移m个单位
y=a(x-h+m)2+k
左+
右-
方法二:
y=ax2+bx+c左右平移时,给每一个x都加m或减m.
向左平移m个单位
规律:
向右平移m个单位
y=a(x+m)2+b(x+m)+c
y=a(x-m)2+b(x-m)+c
左+
右-
基础点 5
二次函数与一元二次方程、不等式的关系
1.二次函数与一元二次方程的关系
(1)抛物线与x轴有两个交点?b2-4ac >0?方程ax2+bx+c=0有两个不相等的实数根;
(2)抛物线与x轴有一个交点?b2-4ac=0?方程ax2+bx+c=0有两个相等的实数根;
(3)抛物线与x轴无交点?b2-4ac<0?方程ax2+bx+c=0无实数根.
2. 二次函数与不等式的关系
(1)ax2+bx+c>0的解集?函数y=ax2+bx+c的图象位于x轴上方对应的点的横坐标的取值范围;
(2)ax2+bx+c<0的解集?函数y=ax2+bx+c的图象位于x轴下方对应的点的横坐标的取值范围.
??????????
练
提
分
必
抛物线y=x2+6x+8与x轴交点坐标为______________________;
当x2+6x+8=0时,x的值为________;
当x2+6x+8>0时,x的取值范围为_____________;
x2+6x+8<0时,x的取值范围为___________.
(-2,0)或(-4,0)
-2或-4
x<-4或x>-2
-4例1 在探究二次函数图象性质的过程中,x与y的对应值如下表:
重难点精讲优练
类型 1
二次函数的顶点坐标、对称轴与增减性
x … -1 0 1 2 3 …
y … 0 -3 -4 -3 0 …
(1)表中二次函数表达式为______________;
(2)函数图象开口向________,顶点坐标为________,对称轴为________;
(3)当x=____时,函数取最小值,最小值为________;
x … -1 0 1 2 3 …
y … 0 -3 -4 -3 0 …
y=x2-2x-3
上
(1,-4)
x=1
1
-4
(4)函数图象与y轴交点坐标为__________,与x轴交点坐标为_________________;
(5)画出此函数图象;
(0,-3)
(-1,0),(3,0)
例1题图
例1题解图
(6)根据图象回答:x取何值时,y>0;x取何值时,y<0;x取何值时,y随x的增大而增大;x取何值时,y随x的增大而减小?
当x<-1或x>3时,y>0;当-1<x<3时,y<0;当x>1时,y随x的增大而增大;当x<1时,y随x的增大而减小.
练习1 已知:抛物线y=x2-3kx+2k+.
(1)当顶点在y轴上时,k的值为________;
(2)当顶点在x轴上时,k的值为________;
(3)当函数图象经过原点时,k的值为________;
(4)当函数图象与x轴的两个交点在y轴的两侧时,k的取值范围为________.
0
解法提示:
(1)∵抛物线y=x2-3kx+2k+ 顶点在y轴上,
∴-3k=0,解得k=0;
(2)∵抛物线y=x2-3kx+2k+ 在x轴上,
∴b2-4ac=0,
∴(-3k)2-4×1×(2k+ )=0,
解得k=1或k=- ;
(3)抛物线y=x2-3kx+2k+ 经过原点,
∴2k+ =0,解得x=- ;
(4)设抛物线y=x2-3kx+2k+ 的两个交点坐标为(x1,0),(x2,0),
∵抛物线与x轴的两个交点在y轴的两侧,
∴x1x2<0,
∴x1x2= = <0,即k<- .
变式拓展 已知:二次函数y=x2+bx+c(b,c为常数).
(1)当b=2,c=-3时,求二次函数的最小值;
(2)当c=b2时,若在自变量x的值满足 b≤x≤b+3的情况下,与其对应的函数值y的最小值为21,求此时二次函数的解析式.
解:(1)当b=2,c=-3时,二次函数的解析式为y=x2+2x-3,即y=(x+1)2-4,
∴当x=-1时,二次函数取得最小值-4;
(2)当c=b2时,二次函数的解析式为y=x2+bx+b2,其图象是开口向上,对称轴为x=- 的抛物线,
①若- <b,即b>0,
∴当b≤x≤b+3时,y随x的增大而增大,
∴当x=b时,y最小值=b2+b·b+b2=3b2,
∴3b2=21,解得b1=- (舍),b2= .
∴二次函数解析式为y=x2+ x+7;
②若b≤- ≤b+3,即-2≤b≤0,
∴当x=- 时,y最小值=(- )2+b·(- )+b2= b2,
∴ b2=21,解得b1=-2 (舍),b2=2 (舍);
③若- >b+3,即b< -2
∴当b≤x≤b+3时,y随x的增大而减小,
∴当x=b+3时,y最小值=(b+3)2+b(b+3)+b2=3b2+9b+9,∴3b2+9b+9=21,即b2+3b-4=0,解得b1=1(舍),b2=-4,∴二次函数解析式为y=x2-4x+16,
综上所述,b= 或b=-4,
∴此时二次函数的解析式为y=x2+ x+7或y=x2-4x+16.
类型 2
二次函数图象与系数a、b、c的关系
例2题图
C
例2 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc<0;②a+b+c<0;③4a+c>2b;④2a-b=0;⑤m(am+b)+b<a(m≠-1),其中,正确结论的个数为( )
A. 2个 B. 3个 C. 4个 D. 5个
【解析】∵抛物线开口向下,∴a<0,∵抛物线的对称轴为直线x=- =-1<0,∴b=2a,∴b<0,∵抛物线与y轴的交点在x轴上方,∴c>0,∴abc>0,∴①错误;∵x=1时,y<0,∴a+b+c<0,∴②正确;∵抛物线的对称轴为直线x=-1,抛物线与x轴的一个交点在点(0,0)和(1,0)之间,∴抛物线与x轴的另一个交点在点(-3,0)和(-2,0)之间,∴当x=-2时,y>0,∴4a-
2b+c>0,∴③正确;∵抛物线对称轴x=- =-1.∴b=2a,即2a-b=0,∴④正确;∵抛物线的对称轴为直线x=-1,∴当x=-1时,y有最大值,∴am2+bm+c<a-b+c(m≠-1),∴m(am+b)<a-b(m≠-1),∴⑤正确;综上所述,正确的结论有②③④⑤.
A
练习2 已知二次函数y=ax2+bx+c的图象与x轴交于点(-2,0)、(x2,0),且1<x2<2,与y轴正半轴的交点在(0,2)下方,在下列结论中:①b<0,② 4a-2b+c=0,③2a-b+1<0,④b<a<c.其中,正确的结论是( )
A. ①② B. ③④ C. ①②③ D. ①②④
【解析】画出图象如解图,
∵开口向下,∴a<0,∵x=- <0,∴b<0,∴①正确;根据二次函数y=ax2+bx+c的图象与x轴交于点(-2,0)、(x2,0),且1<x2<2,与y轴的正半轴的交点在(0,2)的下方,把x=-2代入得:4a-2b+c=0,∴②正确;由4a-2b+c=0得2a-b=-
例2题解图
而0<c<2,∴-1<- <0,∴-1<2a-b<0,∴2a-b+1>0,∴③错误;∵图象与x轴两交点为(-2,0),(x2,0),且1<x2<2,对称轴x=- =- ,则对称轴- <- <0,且a<0,∴-a>-b,∴a<b<0,由抛物线与y轴的正半轴的交点在(0,2)的下方,得c>0,即a<b<c,∴④错误;∴正确的结论为①②.
类型 3
二次函数与一元二次方程的关系
例3 已知抛物线y=(x-m)2-(x-m),其中m是常数.
(1)求证:不论m为何值,该抛物线与x轴一定有两个公共点;
(2)若该抛物线的对称轴为直线x= .
①求该抛物线的函数解析式;②把该抛物线沿y轴向上平移多少个单位长度后,得到的抛物线与x轴只有一个公共点
【自主解答】(1)证明:
∵y=(x-m)2-(x-m)=x2-(2m+1)x+m2+m,
∴b2-4ac=[-(2m+1)]2-4×1×(m2+m)=4m2
+4m+1-4m2-4m=1>0,
∴不论m为何值,该抛物线与x轴一定有两个公共点;
(2)解:①∵y=x2-(2m+1)x+m2+m的对称轴为直线x=- = ,
抛物线对称轴为直线x= ,
∴ = ,
解得m=2,
∴抛物线解析式为y=x2-5x+6;
②设抛物线沿y轴向上平移k个单位长度后,得到的抛物线与x轴只有一个公共点,则平移后抛物线的解析式为
y=x2-5x+6+k.
∵抛物线y=x2-5x+6+k与x轴只有一个公共点,
∴Δ=52-4(6+k)=0,
∴k= ,
即把该抛物线沿y轴向上平移 个单位长度后,得到的抛物线与x轴只有一个公共点.
练习3 (2017张家界节选)已知抛物线c1的顶点为A(-1,4),与y轴的交点为D(0,3).
(1)求c1的解析式;
(2)若直线l1:y=x+m与c1仅有唯一的交点,求m的值;
(3)若抛物线c1关于y轴对称的抛物线记作c2,平行于x轴的直线记作l2:y=n.试结合图形回答:当n为何值时,l2与c1和c2共有:①两个交点;②三个交点;③四个交点.
解:(1)∵抛物线c1的顶点为A(-1,4),
∴设抛物线c1的解析式为y=a(x+1)2+4,
∵点D(0,3)在抛物线上,
∴a(0+1)2+4=3,
∴a=-1,
则抛物线c1的解析式为y=-(x+1)2+4,
即y=-x2-2x+3;
(2) 由题意可得,
即x2+3x+m-3=0,
∵直线与抛物线仅有唯一的交点,
∴b2-4ac=9-4(m-3)=0,解得m= ;
(3)根据题意可得抛物线c1:y=-(x+1)2+4关于y轴对称的抛物线c2的解析式为:y=-(x-1)2+4.
①由图象可得当n=4时,直线y=4经过两抛物线顶点(-1,4),(1,4),此时直线y=4与抛物线有两个交点;
②当n=3时,直线y=3,经过两抛物线的交点D(0,3),此时直线y=3与抛物线有三个交点;
③当n<3或3<n<4时,直线y=n与抛物线有四个交点.
第三单元 函数
第13课时 二次函数的图象与性质
基础点 1
二次函数的定义
基础点巧练妙记
形如(a,b,c是常数,a≠0)的函数.特别地,当a≠0,b=c=0时,y=ax2是二次函数的特殊形式
基础点 2
二次函数的图象与性质
1.根据函数解析式判断函数性质及图象
二次函数y=ax2+bx+c(a≠0)
判断
函数
性质 对称轴 直接运用公式x=①________求解
注:还可利用x=(其中x1、x2为y值相等的两个点对应的横坐标)求解
二次函数y=ax2+bx+c(a≠0)
判断
函数
性质 顶点坐标 1. 直接运用顶点坐标公式
②________________求解;
2. 运用配方法将一般式转化为顶点式求解;
3. 将对称轴的x值代入函数表达式求得对应y值
二次函数y=ax2+bx+c(a≠0)
判断
函数
性质 增减性 a>0时,在对轴左侧,y随x的增大而③________;在对称轴右侧,y随x的增大而④________ a<0时,在对称轴⑤________,y随x的增大而增大;在对称轴⑥______,
y随x的增大而减小
减小
增大
左侧
右侧
二次函数y=ax2+bx+c(a≠0)
判断
函数
性质 最值 a>0时,当x=⑦
______时,y的最小值为 ;
离对称轴越近的点函数值越小 a<0时,y的最大值
为⑧________;
离对称轴越近的点函数值越大
二次函数y=ax2+bx+c(a≠0)
判断
函数
图象 a,决定抛物线开口方向 a⑨_____0 开口向上
a<0 开口向下
a,b决定抛物线的对称轴位置 b=0 对称轴为y轴
a、b同号 对称轴为y轴⑩____侧
a、b异号 对称轴为y轴右侧
>
左
二次函数y=ax2+bx+c(a≠0)
判断
函数
图象 c,决定抛物线与y轴交点的位置
c=0 抛物线过原点
c>0 抛物线与y轴交于?______半轴
c<0 抛物线与y轴交于?______半轴
正
负
二次函数y=ax2+bx+c(a≠0)
判断
函数
图象
b2-4ac,决定抛物线与x轴交点个数 b2-4ac=0 与x轴有唯一交点(顶点)
b2-4ac>0 与x轴有?________交点
b2-4ac<0 与x轴没有交点
两个
二次函数y=ax2+bx+c(a≠0)
判断
特殊
关系 2a+b - 与1比较
2a-b - 与-1比较
b2-4ac 与x轴交点个数
二次函数y=ax2+bx+c(a≠0)
判断
特殊
关系 a+b+c 令x=1,看纵坐标
a-b+c 令x=-1,看纵坐标
4a+2b+c 令x=2,看纵坐标
4a-2b+c 令x=-2,看纵坐标
2.根据函数图象判断相关结论
a?____ 0
b?____0
c<0
b2-4ac>0 a?____0
b=0 c>0
b2-4ac
?____0 a>0
b?____0
c?____0
b2-4ac>0 a < 0
b____0 c < 0
b2-4ac____0
>
>
>
<
<
>
=
>
20
21
a>0
b?____0
c>0
b2-4ac?__0 a?____0
b>0
c?____0
b2-4ac>0 a?____0
b?____0
c=0
b2-4ac>0 a>0
b?____0
c=0
b2-4ac?__0
>
<
>
=
<
>
=
=
1.表达式的三种形式
(1)一般式:y=ax2+bx+c(a、b、c为常数,a≠0);
(2)顶点式:____________(a为常数,a≠0,(h,k)为顶点坐标);
(3)交点式:_________________ (a为常数,a≠0,x1,x2为抛物线与x轴交点的横坐标);
基础点 3
二次函数表达式的确定
y=a(x-h)2+k
y=a(x-x1)(x-x2)
顶点式 一般式 交点式,若顶点在原点,可设为y=ax2.
配方
因式分解
(4)三种表达式之间的关系
2.待定系数法求二次函数的表达式:
(1)对于二次函数y=ax2+bx+c,若系数a、b、c中有一个未知,则代入任意一点坐标;若有两个未知,则代入任意两点坐标;若三个都未知,根据下表所给的点坐标选择适当的表达式
已知 所设表达式
顶点+其他点 y=a(x-h)2+k
与x轴的两个交点+其他点 y=a(x-x1)(x-x2)
与x轴的一个交点+对称轴+其他点
任意三个点 y=ax2+bx+c
(2)联立方程(组),求得系数或常数项;将所得系数或常数项代入表达式即可.
基础点 4
二次函数图象的平移
(1)上加下减:
y=ax2+bx+c
y=ax2+bx+c+m
y=ax2+bx+c+n
向上平移m个单位
向下平移m个单位
(2)左加右减:
方法一:
y=ax2+bx+c
化为
y=a(x-h)2+k
规律:
向右平移m个单位
y=a(x-h-m)2+k
向左平移m个单位
y=a(x-h+m)2+k
左+
右-
方法二:
y=ax2+bx+c左右平移时,给每一个x都加m或减m.
向左平移m个单位
规律:
向右平移m个单位
y=a(x+m)2+b(x+m)+c
y=a(x-m)2+b(x-m)+c
左+
右-
基础点 5
二次函数与一元二次方程、不等式的关系
1.二次函数与一元二次方程的关系
(1)抛物线与x轴有两个交点?b2-4ac >0?方程ax2+bx+c=0有两个不相等的实数根;
(2)抛物线与x轴有一个交点?b2-4ac=0?方程ax2+bx+c=0有两个相等的实数根;
(3)抛物线与x轴无交点?b2-4ac<0?方程ax2+bx+c=0无实数根.
2. 二次函数与不等式的关系
(1)ax2+bx+c>0的解集?函数y=ax2+bx+c的图象位于x轴上方对应的点的横坐标的取值范围;
(2)ax2+bx+c<0的解集?函数y=ax2+bx+c的图象位于x轴下方对应的点的横坐标的取值范围.
??????????
练
提
分
必
抛物线y=x2+6x+8与x轴交点坐标为______________________;
当x2+6x+8=0时,x的值为________;
当x2+6x+8>0时,x的取值范围为_____________;
x2+6x+8<0时,x的取值范围为___________.
(-2,0)或(-4,0)
-2或-4
x<-4或x>-2
-4
重难点精讲优练
类型 1
二次函数的顶点坐标、对称轴与增减性
x … -1 0 1 2 3 …
y … 0 -3 -4 -3 0 …
(1)表中二次函数表达式为______________;
(2)函数图象开口向________,顶点坐标为________,对称轴为________;
(3)当x=____时,函数取最小值,最小值为________;
x … -1 0 1 2 3 …
y … 0 -3 -4 -3 0 …
y=x2-2x-3
上
(1,-4)
x=1
1
-4
(4)函数图象与y轴交点坐标为__________,与x轴交点坐标为_________________;
(5)画出此函数图象;
(0,-3)
(-1,0),(3,0)
例1题图
例1题解图
(6)根据图象回答:x取何值时,y>0;x取何值时,y<0;x取何值时,y随x的增大而增大;x取何值时,y随x的增大而减小?
当x<-1或x>3时,y>0;当-1<x<3时,y<0;当x>1时,y随x的增大而增大;当x<1时,y随x的增大而减小.
练习1 已知:抛物线y=x2-3kx+2k+.
(1)当顶点在y轴上时,k的值为________;
(2)当顶点在x轴上时,k的值为________;
(3)当函数图象经过原点时,k的值为________;
(4)当函数图象与x轴的两个交点在y轴的两侧时,k的取值范围为________.
0
解法提示:
(1)∵抛物线y=x2-3kx+2k+ 顶点在y轴上,
∴-3k=0,解得k=0;
(2)∵抛物线y=x2-3kx+2k+ 在x轴上,
∴b2-4ac=0,
∴(-3k)2-4×1×(2k+ )=0,
解得k=1或k=- ;
(3)抛物线y=x2-3kx+2k+ 经过原点,
∴2k+ =0,解得x=- ;
(4)设抛物线y=x2-3kx+2k+ 的两个交点坐标为(x1,0),(x2,0),
∵抛物线与x轴的两个交点在y轴的两侧,
∴x1x2<0,
∴x1x2= = <0,即k<- .
变式拓展 已知:二次函数y=x2+bx+c(b,c为常数).
(1)当b=2,c=-3时,求二次函数的最小值;
(2)当c=b2时,若在自变量x的值满足 b≤x≤b+3的情况下,与其对应的函数值y的最小值为21,求此时二次函数的解析式.
解:(1)当b=2,c=-3时,二次函数的解析式为y=x2+2x-3,即y=(x+1)2-4,
∴当x=-1时,二次函数取得最小值-4;
(2)当c=b2时,二次函数的解析式为y=x2+bx+b2,其图象是开口向上,对称轴为x=- 的抛物线,
①若- <b,即b>0,
∴当b≤x≤b+3时,y随x的增大而增大,
∴当x=b时,y最小值=b2+b·b+b2=3b2,
∴3b2=21,解得b1=- (舍),b2= .
∴二次函数解析式为y=x2+ x+7;
②若b≤- ≤b+3,即-2≤b≤0,
∴当x=- 时,y最小值=(- )2+b·(- )+b2= b2,
∴ b2=21,解得b1=-2 (舍),b2=2 (舍);
③若- >b+3,即b< -2
∴当b≤x≤b+3时,y随x的增大而减小,
∴当x=b+3时,y最小值=(b+3)2+b(b+3)+b2=3b2+9b+9,∴3b2+9b+9=21,即b2+3b-4=0,解得b1=1(舍),b2=-4,∴二次函数解析式为y=x2-4x+16,
综上所述,b= 或b=-4,
∴此时二次函数的解析式为y=x2+ x+7或y=x2-4x+16.
类型 2
二次函数图象与系数a、b、c的关系
例2题图
C
例2 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc<0;②a+b+c<0;③4a+c>2b;④2a-b=0;⑤m(am+b)+b<a(m≠-1),其中,正确结论的个数为( )
A. 2个 B. 3个 C. 4个 D. 5个
【解析】∵抛物线开口向下,∴a<0,∵抛物线的对称轴为直线x=- =-1<0,∴b=2a,∴b<0,∵抛物线与y轴的交点在x轴上方,∴c>0,∴abc>0,∴①错误;∵x=1时,y<0,∴a+b+c<0,∴②正确;∵抛物线的对称轴为直线x=-1,抛物线与x轴的一个交点在点(0,0)和(1,0)之间,∴抛物线与x轴的另一个交点在点(-3,0)和(-2,0)之间,∴当x=-2时,y>0,∴4a-
2b+c>0,∴③正确;∵抛物线对称轴x=- =-1.∴b=2a,即2a-b=0,∴④正确;∵抛物线的对称轴为直线x=-1,∴当x=-1时,y有最大值,∴am2+bm+c<a-b+c(m≠-1),∴m(am+b)<a-b(m≠-1),∴⑤正确;综上所述,正确的结论有②③④⑤.
A
练习2 已知二次函数y=ax2+bx+c的图象与x轴交于点(-2,0)、(x2,0),且1<x2<2,与y轴正半轴的交点在(0,2)下方,在下列结论中:①b<0,② 4a-2b+c=0,③2a-b+1<0,④b<a<c.其中,正确的结论是( )
A. ①② B. ③④ C. ①②③ D. ①②④
【解析】画出图象如解图,
∵开口向下,∴a<0,∵x=- <0,∴b<0,∴①正确;根据二次函数y=ax2+bx+c的图象与x轴交于点(-2,0)、(x2,0),且1<x2<2,与y轴的正半轴的交点在(0,2)的下方,把x=-2代入得:4a-2b+c=0,∴②正确;由4a-2b+c=0得2a-b=-
例2题解图
而0<c<2,∴-1<- <0,∴-1<2a-b<0,∴2a-b+1>0,∴③错误;∵图象与x轴两交点为(-2,0),(x2,0),且1<x2<2,对称轴x=- =- ,则对称轴- <- <0,且a<0,∴-a>-b,∴a<b<0,由抛物线与y轴的正半轴的交点在(0,2)的下方,得c>0,即a<b<c,∴④错误;∴正确的结论为①②.
类型 3
二次函数与一元二次方程的关系
例3 已知抛物线y=(x-m)2-(x-m),其中m是常数.
(1)求证:不论m为何值,该抛物线与x轴一定有两个公共点;
(2)若该抛物线的对称轴为直线x= .
①求该抛物线的函数解析式;②把该抛物线沿y轴向上平移多少个单位长度后,得到的抛物线与x轴只有一个公共点
【自主解答】(1)证明:
∵y=(x-m)2-(x-m)=x2-(2m+1)x+m2+m,
∴b2-4ac=[-(2m+1)]2-4×1×(m2+m)=4m2
+4m+1-4m2-4m=1>0,
∴不论m为何值,该抛物线与x轴一定有两个公共点;
(2)解:①∵y=x2-(2m+1)x+m2+m的对称轴为直线x=- = ,
抛物线对称轴为直线x= ,
∴ = ,
解得m=2,
∴抛物线解析式为y=x2-5x+6;
②设抛物线沿y轴向上平移k个单位长度后,得到的抛物线与x轴只有一个公共点,则平移后抛物线的解析式为
y=x2-5x+6+k.
∵抛物线y=x2-5x+6+k与x轴只有一个公共点,
∴Δ=52-4(6+k)=0,
∴k= ,
即把该抛物线沿y轴向上平移 个单位长度后,得到的抛物线与x轴只有一个公共点.
练习3 (2017张家界节选)已知抛物线c1的顶点为A(-1,4),与y轴的交点为D(0,3).
(1)求c1的解析式;
(2)若直线l1:y=x+m与c1仅有唯一的交点,求m的值;
(3)若抛物线c1关于y轴对称的抛物线记作c2,平行于x轴的直线记作l2:y=n.试结合图形回答:当n为何值时,l2与c1和c2共有:①两个交点;②三个交点;③四个交点.
解:(1)∵抛物线c1的顶点为A(-1,4),
∴设抛物线c1的解析式为y=a(x+1)2+4,
∵点D(0,3)在抛物线上,
∴a(0+1)2+4=3,
∴a=-1,
则抛物线c1的解析式为y=-(x+1)2+4,
即y=-x2-2x+3;
(2) 由题意可得,
即x2+3x+m-3=0,
∵直线与抛物线仅有唯一的交点,
∴b2-4ac=9-4(m-3)=0,解得m= ;
(3)根据题意可得抛物线c1:y=-(x+1)2+4关于y轴对称的抛物线c2的解析式为:y=-(x-1)2+4.
①由图象可得当n=4时,直线y=4经过两抛物线顶点(-1,4),(1,4),此时直线y=4与抛物线有两个交点;
②当n=3时,直线y=3,经过两抛物线的交点D(0,3),此时直线y=3与抛物线有三个交点;
③当n<3或3<n<4时,直线y=n与抛物线有四个交点.
同课章节目录
