人教版高中物理 选修3-1 1.9 带电粒子在磁场中运动 课件:27张PPT
文档属性
| 名称 | 人教版高中物理 选修3-1 1.9 带电粒子在磁场中运动 课件:27张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2018-11-11 12:37:55 | ||
图片预览




文档简介
课件27张PPT。思考1:
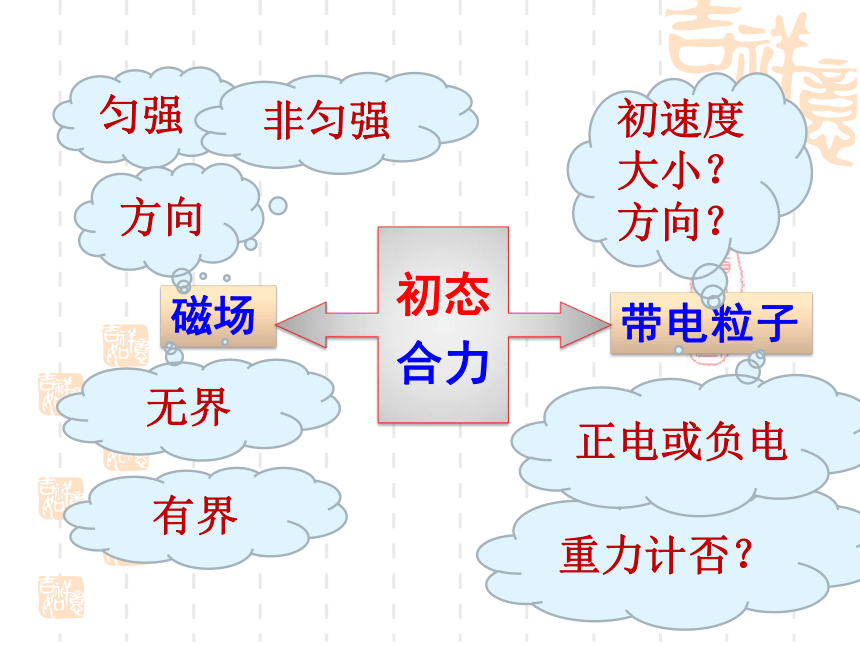
带电粒子在磁场中可能做怎样的运动?磁场带电粒子匀强非匀强有界初态
合力初速度大小?方向?重力计否?正电或负电无界方向带电粒子(不计重力)
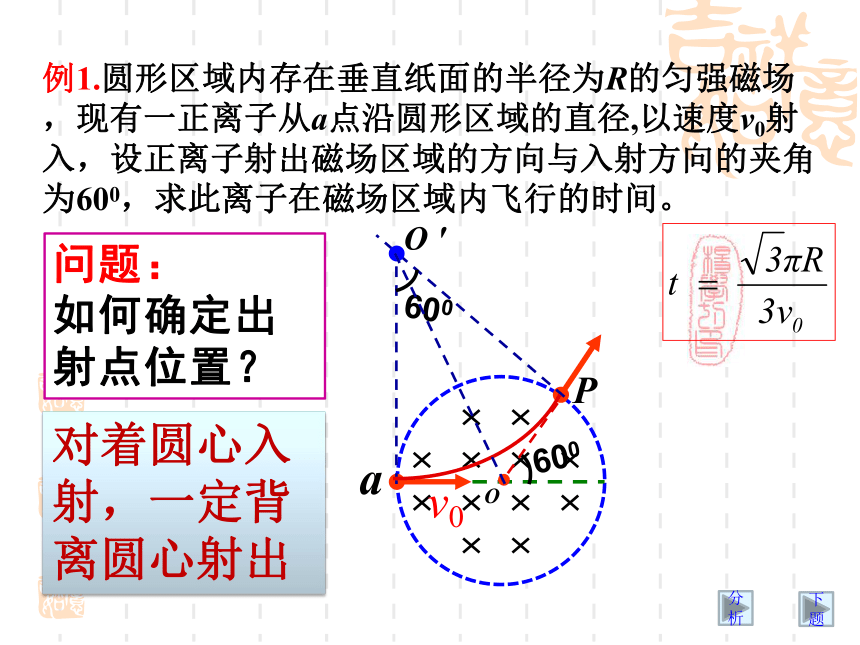
垂直射入圆形匀强磁场中运动1.对心飞入问题例1.圆形区域内存在垂直纸面的半径为R的匀强磁场,现有一正离子从a点沿圆形区域的直径,以速度v0射入,设正离子射出磁场区域的方向与入射方向的夹角为600,求此离子在磁场区域内飞行的时间。OPO ′分析下题对着圆心入射,一定背离圆心射出av0问题:
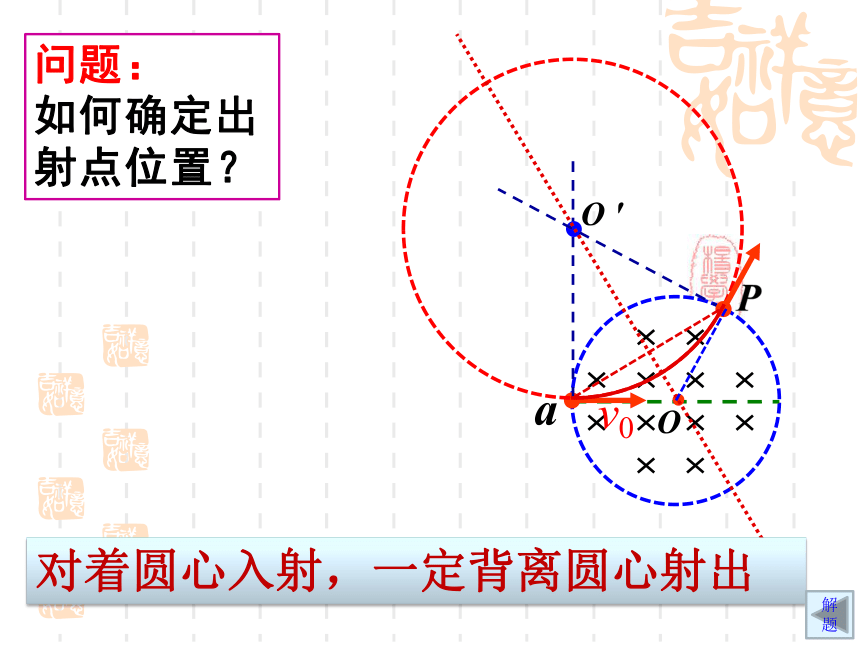
如何确定出射点位置??OO ′对着圆心入射,一定背离圆心射出解题问题:
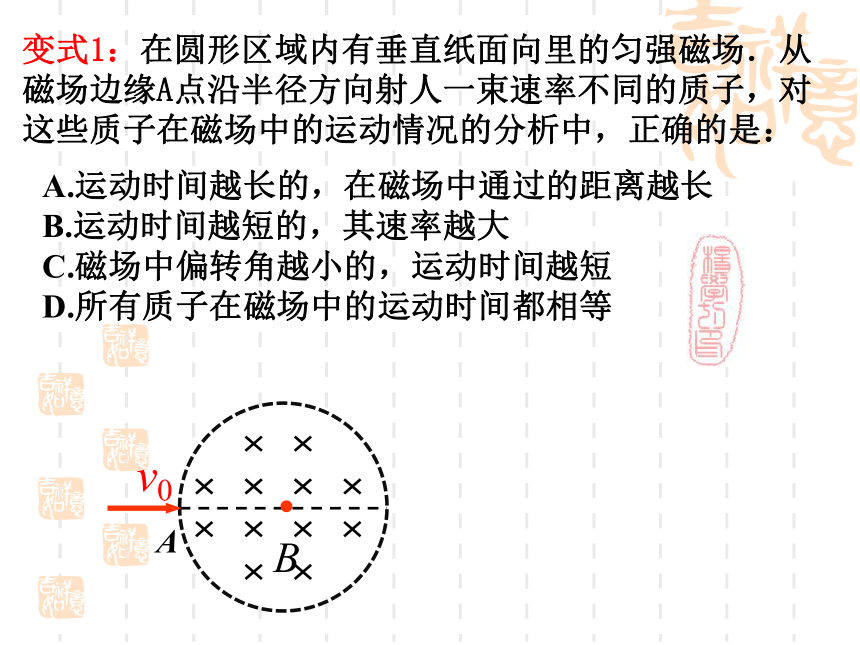
如何确定出射点位置?av0变式1:在圆形区域内有垂直纸面向里的匀强磁场.从磁场边缘A点沿半径方向射人一束速率不同的质子,对这些质子在磁场中的运动情况的分析中,正确的是: A.运动时间越长的,在磁场中通过的距离越长
B.运动时间越短的,其速率越大
C.磁场中偏转角越小的,运动时间越短
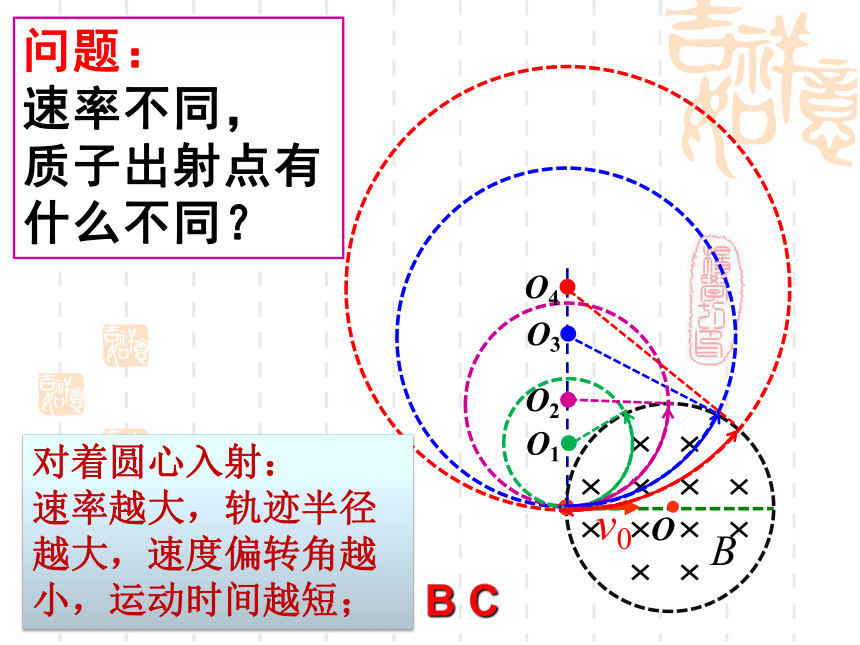
D.所有质子在磁场中的运动时间都相等v0B?OO3问题:
速率不同,
质子出射点有什么不同?v0对着圆心入射:
速率越大,轨迹半径越大,速度偏转角越小,运动时间越短;B C1.对心飞入问题小结:
对着圆心入射,一定背离圆心射出。
也叫“径进径出”。2.最值问题例2.在直角坐标系xOy中,有一半径为R的圆形磁场区域,磁感强度为B,磁场方向垂直xOy平面指向纸内,该区域的圆心坐标为(R,0)。如图所示,有一个质量为m、带电量为-q的离子,从点(0,R/2)沿x轴正方向射入磁场,离子从射入到射出磁场通过了该磁场的最大距离,不计重力影响。求离子射出磁场区域时的速度。 O2O1vPQv问题:
…最大距离是多少?变式1:真空中半径为R=3×10-2m的圆形区域内,有一磁感应强度为B=0.2T的匀强磁场,方向如图所示一带正电的粒子以初速度v0=106m / s 从磁场边界上直径 ab 一端 a 点处射入磁场,已知该粒子比荷为q/m=108C / kg ,不计粒子重力,求:
(1)粒子在磁场中作匀速圆周运动的半径是多少?
(2)若要使粒子飞离磁场时有最大偏转角,求入射时速度方向与ab的夹角θ及粒子的最大偏转角β.
分析下题问题3:
最长运动时间如何求解?r =5×10-2mo粒子带正电
磁场无边界问题1:
入射速度方向不同,运动轨迹位置有什么不同?问题2:
什么时候偏转角最大?解题变式2.(2017全国)如图,虚线所示的圆形区域内存在一垂直于纸面的匀强磁场,P为磁场边界上的一点,大量相同的带电粒子以相同的速率经过P点,在纸面内沿不同的方向射入磁场,若粒子射入速度为 v1,这些粒子在磁场边界的出射点分布在六分之一圆周上;若粒子射入速度为 v2,相应的出射点分布在三分之一圆周上,不计重力及带电粒子之间的相互作用,则 v2:v1为
问题2:
…出射点分布在六分之一圆周上,意味着什么?假设:粒子带正电
磁场垂直纸面向外问题1:
磁场方向、粒子正负未知,怎么办?问题2:
…出射点分布在六分之一圆周上,意味着什么?问题2:
…出射点分布在六分之一圆周上,意味着什么?θCRr2.最值问题小结:
解题关键——抓弦长3.从圆心出发问题例3:一光滑绝缘圆形水平桌面,处于竖直向下的匀强磁场中,圆心O点放置一带电小球。已知桌面半径为r,小球质量为m、电荷量为q,磁场的磁感应强度大小为B。小球从O点以某一速度,沿OA方向,开始运动,经一定时间从桌子边缘P点(未画出)滑离桌面,已知速度偏转角为600,如图所示;求带电小球的速度大小?
分析下题P小结问题:
如何确定出射点位置?解题变式:(2004全国)一匀磁场,磁场方向垂直于xy平面,在xy平面上,磁场分布在以O为中心的一个圆形区域内.一个质量为m、电荷量为q的带电粒子,由原点O开始运动,初速为v,方向沿x正方向.后来,粒子经过y轴上的P点,此时速度方向与y轴的夹角为300,P到O的距离为L,如图所示.不计重力的影响。求:
(1)磁场的磁感强度B的大小;
(2)xy平面上磁场区域的半径R;A问题:
如何确定运动轨迹?3.从圆心出发问题小结:
先画整圆,找到粒子离场点思考2:
带电粒子在有界磁场中问题求解的基本思路是什么?总结:技能上:找圆心→定半径→画轨迹。方法上:“眼前无圆,心中有圆” 。
练习
带电粒子在磁场中可能做怎样的运动?磁场带电粒子匀强非匀强有界初态
合力初速度大小?方向?重力计否?正电或负电无界方向带电粒子(不计重力)
垂直射入圆形匀强磁场中运动1.对心飞入问题例1.圆形区域内存在垂直纸面的半径为R的匀强磁场,现有一正离子从a点沿圆形区域的直径,以速度v0射入,设正离子射出磁场区域的方向与入射方向的夹角为600,求此离子在磁场区域内飞行的时间。OPO ′分析下题对着圆心入射,一定背离圆心射出av0问题:
如何确定出射点位置??OO ′对着圆心入射,一定背离圆心射出解题问题:
如何确定出射点位置?av0变式1:在圆形区域内有垂直纸面向里的匀强磁场.从磁场边缘A点沿半径方向射人一束速率不同的质子,对这些质子在磁场中的运动情况的分析中,正确的是: A.运动时间越长的,在磁场中通过的距离越长
B.运动时间越短的,其速率越大
C.磁场中偏转角越小的,运动时间越短
D.所有质子在磁场中的运动时间都相等v0B?OO3问题:
速率不同,
质子出射点有什么不同?v0对着圆心入射:
速率越大,轨迹半径越大,速度偏转角越小,运动时间越短;B C1.对心飞入问题小结:
对着圆心入射,一定背离圆心射出。
也叫“径进径出”。2.最值问题例2.在直角坐标系xOy中,有一半径为R的圆形磁场区域,磁感强度为B,磁场方向垂直xOy平面指向纸内,该区域的圆心坐标为(R,0)。如图所示,有一个质量为m、带电量为-q的离子,从点(0,R/2)沿x轴正方向射入磁场,离子从射入到射出磁场通过了该磁场的最大距离,不计重力影响。求离子射出磁场区域时的速度。 O2O1vPQv问题:
…最大距离是多少?变式1:真空中半径为R=3×10-2m的圆形区域内,有一磁感应强度为B=0.2T的匀强磁场,方向如图所示一带正电的粒子以初速度v0=106m / s 从磁场边界上直径 ab 一端 a 点处射入磁场,已知该粒子比荷为q/m=108C / kg ,不计粒子重力,求:
(1)粒子在磁场中作匀速圆周运动的半径是多少?
(2)若要使粒子飞离磁场时有最大偏转角,求入射时速度方向与ab的夹角θ及粒子的最大偏转角β.
分析下题问题3:
最长运动时间如何求解?r =5×10-2mo粒子带正电
磁场无边界问题1:
入射速度方向不同,运动轨迹位置有什么不同?问题2:
什么时候偏转角最大?解题变式2.(2017全国)如图,虚线所示的圆形区域内存在一垂直于纸面的匀强磁场,P为磁场边界上的一点,大量相同的带电粒子以相同的速率经过P点,在纸面内沿不同的方向射入磁场,若粒子射入速度为 v1,这些粒子在磁场边界的出射点分布在六分之一圆周上;若粒子射入速度为 v2,相应的出射点分布在三分之一圆周上,不计重力及带电粒子之间的相互作用,则 v2:v1为
问题2:
…出射点分布在六分之一圆周上,意味着什么?假设:粒子带正电
磁场垂直纸面向外问题1:
磁场方向、粒子正负未知,怎么办?问题2:
…出射点分布在六分之一圆周上,意味着什么?问题2:
…出射点分布在六分之一圆周上,意味着什么?θCRr2.最值问题小结:
解题关键——抓弦长3.从圆心出发问题例3:一光滑绝缘圆形水平桌面,处于竖直向下的匀强磁场中,圆心O点放置一带电小球。已知桌面半径为r,小球质量为m、电荷量为q,磁场的磁感应强度大小为B。小球从O点以某一速度,沿OA方向,开始运动,经一定时间从桌子边缘P点(未画出)滑离桌面,已知速度偏转角为600,如图所示;求带电小球的速度大小?
分析下题P小结问题:
如何确定出射点位置?解题变式:(2004全国)一匀磁场,磁场方向垂直于xy平面,在xy平面上,磁场分布在以O为中心的一个圆形区域内.一个质量为m、电荷量为q的带电粒子,由原点O开始运动,初速为v,方向沿x正方向.后来,粒子经过y轴上的P点,此时速度方向与y轴的夹角为300,P到O的距离为L,如图所示.不计重力的影响。求:
(1)磁场的磁感强度B的大小;
(2)xy平面上磁场区域的半径R;A问题:
如何确定运动轨迹?3.从圆心出发问题小结:
先画整圆,找到粒子离场点思考2:
带电粒子在有界磁场中问题求解的基本思路是什么?总结:技能上:找圆心→定半径→画轨迹。方法上:“眼前无圆,心中有圆” 。
练习
