4.4 探索三角形相似的条件课时作业(3)
文档属性
| 名称 | 4.4 探索三角形相似的条件课时作业(3) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-11 21:44:53 | ||
图片预览



文档简介
4.4 探索三角形相似的条件课时作业(3)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.如图,点O是△ABC内任一点,点D,E,F分别为OA,OB,OC的中点,则图中相似三角形有( )
A. 1对 B. 2对 C. 3对 D. 4对
2.以下条件不可以判定与相似的是( )
A. B. ,且’
C. ’,’ D. ,且’
3.已知的三边长分别为,,,现在有长度分别为和的木条各一根,要做一个三角形木架与已知三角形相似,那么第三根木条的长度应为( )
A. 20cm B. 25cm C. 30cm D. 35cm
4.如图所示,在正方形网格上有6个三角形:①△ABC;②△BCD;③△BDE;④△BFG;⑤△FGH;⑥△EFK.其中②~⑥中与①相似的是( )
A. ②③④ B. ③④⑤ C. ④⑤⑥ D. ②③⑥
5.如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,若△CEF的面积为18cm2,则S△DGF的值为( )
A. 4cm2 B. 5cm2 C. 6cm2 D. 7cm2
6.如图,在△ABC中,D、E分别是BC、AC上的点,AD与BE相交于点G,若AG:GD=4:1,BD:DC=2:3,则AE:EC的值是( )
A. B. C. D.
7.如图,在△ABC中,AB=BC,∠ABC=90°,BM是AC边中线,点D,E分别在边AC和BC上,DB=DE,EF⊥AC于点F,以下结论:①△BMD≌△DFE;②△NBE∽△DBC;③AC=2DF;④EFAB=CFBC,其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
二、填空题
8.的三边长,,,的三边长,,,则________.
9.如图,在中,,,,则的长是________.
10.一个铝质的三角形框架的三边长分别为24 cm,30 cm,36 cm,要做一个与它相似的铝质三角形的框架,现有长27 cm,45 cm的两根铝材,要求以其中的一根为边,从另一根上截下两段(允许有余材),则截法有______种.
11.如图所示,∠C=∠E=90°,AC=3,AB=4,AE=2,当AD=___时,Rt△ABC∽Rt△ADE.
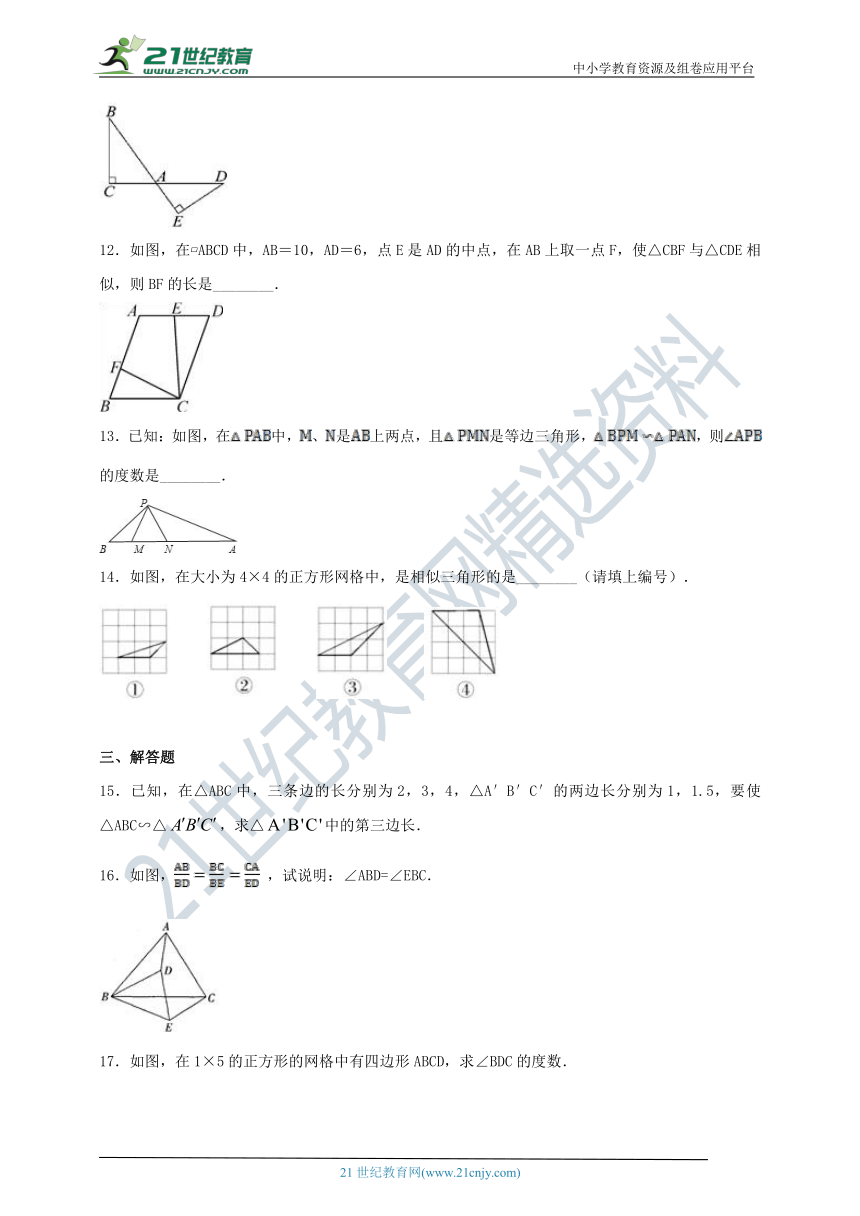
12.如图,在?ABCD中,AB=10,AD=6,点E是AD的中点,在AB上取一点F,使△CBF与△CDE相似,则BF的长是________.
13.已知:如图,在中,、是上两点,且是等边三角形,,则的度数是________.
14.如图,在大小为4×4的正方形网格中,是相似三角形的是________(请填上编号).
三、解答题
15.已知,在△ABC中,三条边的长分别为2,3,4,△A′B′C′的两边长分别为1,1.5,要使△ABC∽△,求△中的第三边长.
16.如图, ,试说明:∠ABD=∠EBC.
17.如图,在1×5的正方形的网格中有四边形ABCD,求∠BDC的度数.
18.如图, . 求证:AB=AE.
19.如图,在△ABC中,点D,E,F分别是CA,AB,BC的中点,求证:△ABC∽△FDE.
20.△ABC和△A′B′C′的各角的度数与各边的长度如图,这两个三角形相似吗?若相似,则相似比是多少?若不相似,请说明理由.
21.如图,在四边形ABCD中,AD、BD相交于点F,点E在BD上,且.
(1)试问:∠BAE与∠CAD相等吗?为什么?
(2)判断△ABE与△ACD是否相似?并说明理由.
22.如图,在4×4的正方形网格中,△ABC和△DEF的顶点都在边长为1的正方形的顶点上.
(1)填空:∠ABC=__________度,BC=_________;
(2)求证:∠C=∠E.
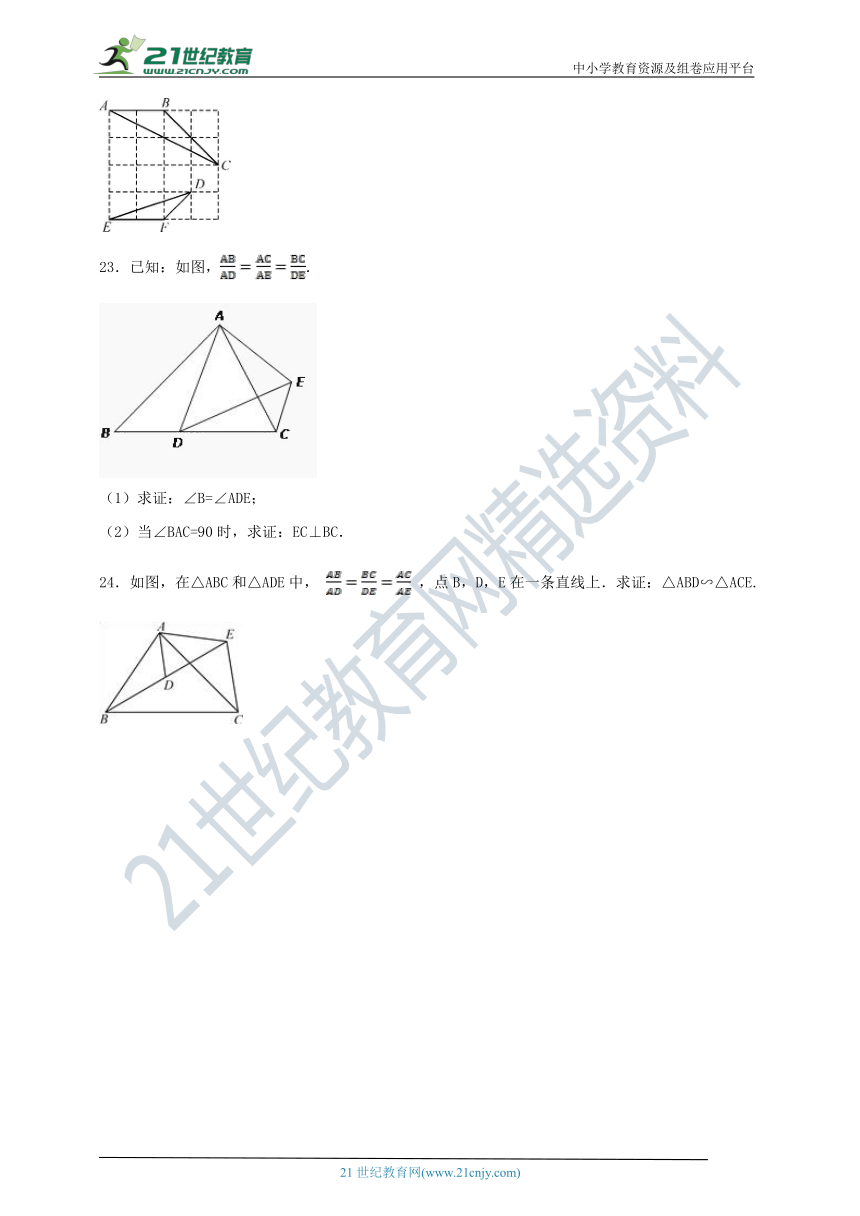
23.已知:如图,.
(1)求证:∠B=∠ADE;
(2)当∠BAC=90时,求证:EC⊥BC.
24.如图,在△ABC和△ADE中, ,点B,D,E在一条直线上.求证:△ABD∽△ACE.
参考答案
1.【考点】相似三角形的判定
【分析】根据点D,E,F分别为OA,OB,OC的中点,可得DE是△AOB的中位线,DF是△AOC的中位线,EF是△BOC的中位线,可得DE//AB,DF//AC,EF//BC,进而可判定△DOE∽△AOD, △DOF∽△AOC, △EOF∽△BOC,根据中位线性质可得,,
继而可得,可判定△DEF∽△ABC.
解:因为点D,E,F分别为OA,OB,OC的中点,
所以DE是△AOB的中位线,DF是△AOC的中位线,EF是△BOC的中位线,
所以DE//AB,DF//AC,EF//BC,
所以△DOE∽△AOD, △DOF∽△AOC, △EOF∽△BOC,
因为DE是△AOB的中位线,DF是△AOC的中位线,EF是△BOC的中位线,
所以,,
所以,
所以△DEF∽△ABC,
因此有四对相似三角形,
故选D.
【点睛】本题主要考查相似三角形的判定,解决本题的关键是要熟练掌握相似三角形的判定方法.
2.【考点】相似三角形的判定
【分析】根据三组对应边的比相等的两个三角形相似可对进行判断;根据两组对应边的比相等且夹角对应相等的两个三角形相似可对、进行判断;根据有两组角对应相等的两个三角形相似可对进行判断.
解:、因为,所以,即选项可以判断与相似;
、因为,,所以,即选项可以判断与相似;
、因为,,所以,即选项可以判断与相似;
、因为,,所以,即选项不可以判断与相似.
故选:.
【点睛】本题考查了相似三角形的判定:三组对应边的比相等的两个三角形相似;两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.
3.【考点】相似三角形的判定
【分析】先判断出第三根木条与50cm的边长是对应边,再根据相似三角形对应边成比例列式计算即可得解.
解:∵
∴第三根木条与50cm的边长是对应边,设为xcm,
∴
解得x=25cm.
故选B.
【点睛】考查相似三角形的性质,掌握相似三角形对应角相等,对应边的比相等是解题的关键.
4.【考点】相似三角形的判定
【分析】先根据勾股定理计算出三角形各边的长度,再根据三边对应成比例两三角形相似进行判定即可.
解:设第个小正方形的边长为1,则△ABC的各边长分别为1,,,则
②△BCD的各边长分别为1,,,
③△BDE的各边长分别为2,,,(为△ABC对应各边长的2倍),
④△BFG的各边长分别为5,,,(为△ABC对应各边长的?倍),
⑤△FGH的各边长分别为2,,(为△ABC对应各边长的?倍),
⑥△EFK的各边长分别为3,,,
根据三组对应边的比相等的两个三角形相似得到与三角形①相似的是③④⑤. 故选B.
【点睛】本题主要考查相似三角形的判定定理,解决本题的关键是要熟练掌握相似三角形的判定方法.
5.【考点】相似三角形的判定
【分析】作GH⊥BC于H交DE于M,根据三角形中位线定理得到DE∥BC,DE=BC,证明△GDF∽△GBC,根据相似三角形的性质、三角形的面积公式计算.
解:作GH⊥BC于H交DE于M,
∵DE是△ABC的中位线,
∴DE∥BC,DE=BC,
∵F是DE的中点,
∴DF=BC,
∵DF∥BC,
∴△GDF∽△GBC,
∴==,
∴=,
∵DF=FE,
∴S△DGF=×△CEF的面积=6cm2,
故选:C.
【点睛】本题考查的是相似三角形的判定和性质、三角形中位线定理,掌握相似三角形的判定定理和性质定理是解题的关键.
6.【考点】相似三角形的判定
【分析】如图,过点D作DF//AC交BE于点F,则△BCE△BDF, △GDF△GAE.再根据相似三角形的性质分别得到EC=DF,AE=4DF.所以AE:EC=.
解:如图,过点D作DF//AC交BE于点F,
则△BCE△BDF, △GDF△GAE.
∴=,,
∵AG:GD=4:1,BD:DC=2:3,
∴EC=DF,AE=4DF.
∴AE:EC=4DF:DF=4:=.
故选C.
【点睛】本题考查了相似三角形的性质和判定,根据题意正确作出辅助线是解题的关键.
7.【考点】相似三角形的判定
【分析】根据全等三角形的判定和性质及相似三角形的判定和性质即可.
解:∵AB=BC,∠ABC=90°,BM是AC边中线,
∴∠MBC=∠C =45°,BM=AM=MC
∵DB=DE,
∴∠DBE=∠DEB
即∠DBM+45°=∠CDE+45°.
∴∠DBM=∠CDE.
∵EF⊥AC,
∴∠DFE=∠BMD=90°
在△BMD和△DFE中
∴△BMD≌△DFE.
故①正确.
由① 可得∠DBE=∠DEB,∠MBC=∠C
∴△NBE∽△DCB,
故②错,对应字母没有写在对应的位置上.
∵△BMD≌△DFE,
∴BM=DF,
∵BM=AM=MC,
∴AC=2BM,
∴AC=2DF.
故③正确
易证△EFC∽△ABC,所以=,
∴EFAB=CFBC
故④正确
故选C.
【点睛】本题主要考查的是全等三角形、相似三角形性质和判定,等腰直角三角形的性质,
掌握基础知识是解题的关键.
8.【考点】相似三角形的判定
【分析】根据已知条件可知两三角形的对应边成的比值相等,由此即可得答案.
解:∵AB=5,BC=4,AC=3, A'B'=10,B'C'=8,A'C'=6,
∴AB: A′B′=BC:B′C′=AC:A′C′=1:2,
∴Rt△ABC∽Rt△A′B′C′,
故答案为:∽.
【点睛】本题考查了相似三角形的判定,熟知三边的比对应相等的两个三角形相似是解题的关键.
9.【考点】相似三角形的判定
【分析】由平行可得到DE:BC=AD:AB,由DE=6可求得BC.
解:∵DE∥BC,
∴DE:BC=AD:AB=1:3,
即6:BC=1:3,
∴BC=18.
故答案为:18.
【点睛】考查相似三角形的判定与性质,掌握相似三角形的性质是解题的关键.
10.【考点】相似三角形的判定
【分析】先判断出两根铝材哪根为边,需截哪根,再根据相似三角形的对应边成比例求出另外两边的长,由另外两边的长的和与另一根铝材相比较即可.
解:∵两根铝材的长分别为27cm,45cm,若45cm为一边时,
则另两边的和为27cm,27<45,不能构成三角形,
∴必须以27cm为一边,45cm的铝材为另外两边,
设另外两边长分别为x,y,则:
若27cm与24cm相对应时,
,
解得:x=33.75cm,y=40.5cm,
x+y=33.75+40.5=74.25cm>45cm,故不成立,
若27cm与36cm相对应时,
,
解得:x=22.5cm,y=18cm,x+y=22.5+18=40.5cm<45cm,成立,
若27cm与30cm相对应时,
, 解得:x=32.4cm,y=21.6cm,x+y=32.4+21.6=54cm>45cm,故不成立,故只有一种截法.
【点睛】本题主要考查相似三角形的性质及三角形成立的条件,解决本题的关键是要根据三角形的边长分情况讨论,利用相似三角形三边对应成比例列式求解.
11.【考点】相似三角形的判定
解:由于∠C=∠E=90°,,根据两角对应相等,两三角形相似得:Rt△ABC∽Rt△ADE.所以:,即:AD=.
故答案:.
12.【考点】相似三角形的判定
解:∵在平行四边形ABCD中,AB=10,AD=6,E是AD的中点,
∴CD=10,BC=6,DE=3.
∵△CBF∽△CDE,
∴BF:DE=BC:DC,
∴BF=6÷10×3=1.8.
13.【考点】相似三角形的判定
【分析】由可得出∠BPM=∠A,进而由等边三角形性质和角的转化可得.
解:∵
∴∠BPM=∠A,
∵是等边三角形
∴∠A+∠APN=60°,∠APN+∠MPN=60°
∴∠APB=∠BPM+∠MPN+∠APN=60°+60=120°.
【点睛】本题考查了相似三角形的性质,熟悉换算是解决本题的关键.
14.【考点】相似三角形的判定
解:∵①中的三角形的三边分别是:2, , ;
②中的三角形的三边分别是:3, , ;
③中的三角形的三边分别是:2,2,2;
④中的三角形的三边分别是:3, ,4;
∵①与③中的三角形的三边的比为:1: :
∴①与③相似.
故答案为:①③.
【点睛】相似三角形的判定方法:(1)平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;
(2)三边法:三组对应边的比相等的两个三角形相似;
(3)两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;
(4)两角法:有两组角对应相等的两个三角形相似.
15.【考点】相似三角形的判定
【分析】此题主要应用两三角形相似的判定定理,三边对应成比例的两个三角形相似,分析作答即可.
解:已知在△ABC中,三条边的长分别为2,3,4,△ 的两边长分别为1,1.5,可以看出,△的两边分别为△ABC的两边长的一半,因此要使△ABC∽△需两三角形各边对应成比例,则第三边长就为4的一半即2.
16.【考点】相似三角形的判定
【分析】先根据三边对应成比例,两三角形相似可判定△ABC∽△DBE,再根据相似三角形对应角相等可得: ∠ABC=∠DBE,然后根据角的和差关系可得∠ABC-∠DBC=∠DBE-∠DBC,继而可证: ∠ABD=∠CBE.
解:∵,
∴△ABC∽△DBE,
∴∠ABC=∠DBE,
∴∠ABC-∠DBC=∠DBE-∠DBC,
即∠ABD=∠CBE.
【点睛】本题主要考查相似三角形的判定和性质,解决本题的关键是要熟练掌握相似三角形的判定和性质.
17.【考点】相似三角形的判定
【分析】先根据勾股定理计算出网格中三角形的各个边长,然后求出各边比值,根据三边对应成比例两三角形相似可得△ABD∽△DCB,然后再可得∠BDC=∠BAD=135°.
解:由图知AB=,AD=1,BD=,BC=5,DC=,
∴,,,
∴,
∴△ABD∽△DCB,
∴∠BDC=∠BAD=135°.
【点睛】本题主要考查相似三角形的判定定理,解决本题的关键是要熟练掌握相似三角形的判定方法.
18.【考点】相似三角形的判定
【分析】根据三边对应成比例的两个三角形相似,可得△ADE∽△CAB,再根据相似三角形的对应角相等可得到∠AED=∠ABC,从而可证AB=AE.
解:∵,
∴△ADE∽△CAB,(三条对应边成比例,两三角形相似),
∴∠AED=∠ABC,
∴AB=AE.
19.【考点】相似三角形的判定
【分析】根据三角形中位线的判定可得:DE,DF,EF,是△ABC的中位线,然后根据中位线的性质可得:,最后根据三边对应成比例,两三角形相似可判定△ABC∽△FDE.
解:∵点D,E,F分别是CA,AB,BC的中点,
∴,
∴△ABC∽△FDE.
【点睛】本题主要考查三角形中位线的判定和性质,相似三角形的判定,解决本题的关键是要熟练掌握中位线的判定和性质,相似三角形的判定.
20.【考点】相似三角形的判定
【分析】由已知可推出两个图形对应角相等,对应边成比例,所以相似.
解:∵∠A=180°-∠B-∠C=82.5°,∠A′=180°-∠B′-∠C′=82.5°,
∴∠A=∠A′,∠B=∠B′,∠C=∠C′.
又∵,,,
∴.
∴根据相似图形的定义可知,△ABC与△A′B′C′相似,相似比是3∶1.
【点睛】本题考核知识点:相似判定. 解题关键点:理解相似的条件.
21.【考点】相似三角形的判定
【分析】(1)、根据,得出△ABC∽△AED,从而说明∠BAC=∠EAD,然后得出答案;(2)、根据得出,结合∠BAE=∠CAD得出三角形相似.
解:(1)∠BAE与∠CAD相等.
在△ABC和△AED中,
∵,
∴△ABC∽△AED,
∴∠BAC=∠EAD,
∴∠BAE=∠CAD;
(2)△ABE与△ACD相似.
由
得,
在△ABE和△ACD中,
∵,
∠BAE=∠CAD,
∴△ABE∽△ACD.
22.【考点】相似三角形的判定
【分析】(1)根据正方形的对角线可得∠ABC的补角等于45°,即可求出∠ABC=135°,根据BC是正方形的对角线,利用勾股定理进行计算即可.
(2)先根据勾股定理计算出网格中三角形的各个边长,然后求出各边比值,根据三边对应成比例两三角形相似可得△ABD∽△DCB,然后再可得
解:(1) 135° 2
(2) 由图知,AB=2,BC=2,AC=2,DF=,EF=2,DE=,
∴,,,
∴,
∴△DEF∽△ACB,
∴∠C=∠E.
【点睛】本题主要考查相似三角形的判定和性质,解决本题的关键是要熟练掌握相似三角形的判定和性质.
23.【考点】相似三角形的判定
【分析】(1)由相似三角形的判定可得△ABC∽△DEF,再根据相似三角形的性质即可解出;(2) 利用边角的关系证出△ABD∽△ACE,从而得出∠ACE+∠ACD=90°,得出结论.
解:(1)∵
∴△ABC∽△DEF???
∴,
(2)∵BAC=DAE??
∴BAD=CAE?
又∵
∴?
∴△ABD∽△ACE?
∴ABD=ACE
∵BAC=90°
∴ABD+ACD=90°?????
∴ACE+ACD=90°?
即ECBC.
【点睛】本题考查了相似三角形的性质与判定,熟练掌握相似三角形的判定是解题的关键.
24.【考点】相似三角形的判定
【分析】由在△ABC和△ADE中,,可证得△ABC∽△ADE,即可证得∠BAD=∠CAE,又由,即可证得:△ABD∽△ACE.
证明:∵在△ABC和△ADE中,,
∴△ABC∽△ADE,
∴∠BAC=∠DAE,
∴∠BAD=∠CAE,
∵,
∴,
∴△ABD∽△ACE.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.如图,点O是△ABC内任一点,点D,E,F分别为OA,OB,OC的中点,则图中相似三角形有( )
A. 1对 B. 2对 C. 3对 D. 4对
2.以下条件不可以判定与相似的是( )
A. B. ,且’
C. ’,’ D. ,且’
3.已知的三边长分别为,,,现在有长度分别为和的木条各一根,要做一个三角形木架与已知三角形相似,那么第三根木条的长度应为( )
A. 20cm B. 25cm C. 30cm D. 35cm
4.如图所示,在正方形网格上有6个三角形:①△ABC;②△BCD;③△BDE;④△BFG;⑤△FGH;⑥△EFK.其中②~⑥中与①相似的是( )
A. ②③④ B. ③④⑤ C. ④⑤⑥ D. ②③⑥
5.如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,若△CEF的面积为18cm2,则S△DGF的值为( )
A. 4cm2 B. 5cm2 C. 6cm2 D. 7cm2
6.如图,在△ABC中,D、E分别是BC、AC上的点,AD与BE相交于点G,若AG:GD=4:1,BD:DC=2:3,则AE:EC的值是( )
A. B. C. D.
7.如图,在△ABC中,AB=BC,∠ABC=90°,BM是AC边中线,点D,E分别在边AC和BC上,DB=DE,EF⊥AC于点F,以下结论:①△BMD≌△DFE;②△NBE∽△DBC;③AC=2DF;④EFAB=CFBC,其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
二、填空题
8.的三边长,,,的三边长,,,则________.
9.如图,在中,,,,则的长是________.
10.一个铝质的三角形框架的三边长分别为24 cm,30 cm,36 cm,要做一个与它相似的铝质三角形的框架,现有长27 cm,45 cm的两根铝材,要求以其中的一根为边,从另一根上截下两段(允许有余材),则截法有______种.
11.如图所示,∠C=∠E=90°,AC=3,AB=4,AE=2,当AD=___时,Rt△ABC∽Rt△ADE.
12.如图,在?ABCD中,AB=10,AD=6,点E是AD的中点,在AB上取一点F,使△CBF与△CDE相似,则BF的长是________.
13.已知:如图,在中,、是上两点,且是等边三角形,,则的度数是________.
14.如图,在大小为4×4的正方形网格中,是相似三角形的是________(请填上编号).
三、解答题
15.已知,在△ABC中,三条边的长分别为2,3,4,△A′B′C′的两边长分别为1,1.5,要使△ABC∽△,求△中的第三边长.
16.如图, ,试说明:∠ABD=∠EBC.
17.如图,在1×5的正方形的网格中有四边形ABCD,求∠BDC的度数.
18.如图, . 求证:AB=AE.
19.如图,在△ABC中,点D,E,F分别是CA,AB,BC的中点,求证:△ABC∽△FDE.
20.△ABC和△A′B′C′的各角的度数与各边的长度如图,这两个三角形相似吗?若相似,则相似比是多少?若不相似,请说明理由.
21.如图,在四边形ABCD中,AD、BD相交于点F,点E在BD上,且.
(1)试问:∠BAE与∠CAD相等吗?为什么?
(2)判断△ABE与△ACD是否相似?并说明理由.
22.如图,在4×4的正方形网格中,△ABC和△DEF的顶点都在边长为1的正方形的顶点上.
(1)填空:∠ABC=__________度,BC=_________;
(2)求证:∠C=∠E.
23.已知:如图,.
(1)求证:∠B=∠ADE;
(2)当∠BAC=90时,求证:EC⊥BC.
24.如图,在△ABC和△ADE中, ,点B,D,E在一条直线上.求证:△ABD∽△ACE.
参考答案
1.【考点】相似三角形的判定
【分析】根据点D,E,F分别为OA,OB,OC的中点,可得DE是△AOB的中位线,DF是△AOC的中位线,EF是△BOC的中位线,可得DE//AB,DF//AC,EF//BC,进而可判定△DOE∽△AOD, △DOF∽△AOC, △EOF∽△BOC,根据中位线性质可得,,
继而可得,可判定△DEF∽△ABC.
解:因为点D,E,F分别为OA,OB,OC的中点,
所以DE是△AOB的中位线,DF是△AOC的中位线,EF是△BOC的中位线,
所以DE//AB,DF//AC,EF//BC,
所以△DOE∽△AOD, △DOF∽△AOC, △EOF∽△BOC,
因为DE是△AOB的中位线,DF是△AOC的中位线,EF是△BOC的中位线,
所以,,
所以,
所以△DEF∽△ABC,
因此有四对相似三角形,
故选D.
【点睛】本题主要考查相似三角形的判定,解决本题的关键是要熟练掌握相似三角形的判定方法.
2.【考点】相似三角形的判定
【分析】根据三组对应边的比相等的两个三角形相似可对进行判断;根据两组对应边的比相等且夹角对应相等的两个三角形相似可对、进行判断;根据有两组角对应相等的两个三角形相似可对进行判断.
解:、因为,所以,即选项可以判断与相似;
、因为,,所以,即选项可以判断与相似;
、因为,,所以,即选项可以判断与相似;
、因为,,所以,即选项不可以判断与相似.
故选:.
【点睛】本题考查了相似三角形的判定:三组对应边的比相等的两个三角形相似;两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.
3.【考点】相似三角形的判定
【分析】先判断出第三根木条与50cm的边长是对应边,再根据相似三角形对应边成比例列式计算即可得解.
解:∵
∴第三根木条与50cm的边长是对应边,设为xcm,
∴
解得x=25cm.
故选B.
【点睛】考查相似三角形的性质,掌握相似三角形对应角相等,对应边的比相等是解题的关键.
4.【考点】相似三角形的判定
【分析】先根据勾股定理计算出三角形各边的长度,再根据三边对应成比例两三角形相似进行判定即可.
解:设第个小正方形的边长为1,则△ABC的各边长分别为1,,,则
②△BCD的各边长分别为1,,,
③△BDE的各边长分别为2,,,(为△ABC对应各边长的2倍),
④△BFG的各边长分别为5,,,(为△ABC对应各边长的?倍),
⑤△FGH的各边长分别为2,,(为△ABC对应各边长的?倍),
⑥△EFK的各边长分别为3,,,
根据三组对应边的比相等的两个三角形相似得到与三角形①相似的是③④⑤. 故选B.
【点睛】本题主要考查相似三角形的判定定理,解决本题的关键是要熟练掌握相似三角形的判定方法.
5.【考点】相似三角形的判定
【分析】作GH⊥BC于H交DE于M,根据三角形中位线定理得到DE∥BC,DE=BC,证明△GDF∽△GBC,根据相似三角形的性质、三角形的面积公式计算.
解:作GH⊥BC于H交DE于M,
∵DE是△ABC的中位线,
∴DE∥BC,DE=BC,
∵F是DE的中点,
∴DF=BC,
∵DF∥BC,
∴△GDF∽△GBC,
∴==,
∴=,
∵DF=FE,
∴S△DGF=×△CEF的面积=6cm2,
故选:C.
【点睛】本题考查的是相似三角形的判定和性质、三角形中位线定理,掌握相似三角形的判定定理和性质定理是解题的关键.
6.【考点】相似三角形的判定
【分析】如图,过点D作DF//AC交BE于点F,则△BCE△BDF, △GDF△GAE.再根据相似三角形的性质分别得到EC=DF,AE=4DF.所以AE:EC=.
解:如图,过点D作DF//AC交BE于点F,
则△BCE△BDF, △GDF△GAE.
∴=,,
∵AG:GD=4:1,BD:DC=2:3,
∴EC=DF,AE=4DF.
∴AE:EC=4DF:DF=4:=.
故选C.
【点睛】本题考查了相似三角形的性质和判定,根据题意正确作出辅助线是解题的关键.
7.【考点】相似三角形的判定
【分析】根据全等三角形的判定和性质及相似三角形的判定和性质即可.
解:∵AB=BC,∠ABC=90°,BM是AC边中线,
∴∠MBC=∠C =45°,BM=AM=MC
∵DB=DE,
∴∠DBE=∠DEB
即∠DBM+45°=∠CDE+45°.
∴∠DBM=∠CDE.
∵EF⊥AC,
∴∠DFE=∠BMD=90°
在△BMD和△DFE中
∴△BMD≌△DFE.
故①正确.
由① 可得∠DBE=∠DEB,∠MBC=∠C
∴△NBE∽△DCB,
故②错,对应字母没有写在对应的位置上.
∵△BMD≌△DFE,
∴BM=DF,
∵BM=AM=MC,
∴AC=2BM,
∴AC=2DF.
故③正确
易证△EFC∽△ABC,所以=,
∴EFAB=CFBC
故④正确
故选C.
【点睛】本题主要考查的是全等三角形、相似三角形性质和判定,等腰直角三角形的性质,
掌握基础知识是解题的关键.
8.【考点】相似三角形的判定
【分析】根据已知条件可知两三角形的对应边成的比值相等,由此即可得答案.
解:∵AB=5,BC=4,AC=3, A'B'=10,B'C'=8,A'C'=6,
∴AB: A′B′=BC:B′C′=AC:A′C′=1:2,
∴Rt△ABC∽Rt△A′B′C′,
故答案为:∽.
【点睛】本题考查了相似三角形的判定,熟知三边的比对应相等的两个三角形相似是解题的关键.
9.【考点】相似三角形的判定
【分析】由平行可得到DE:BC=AD:AB,由DE=6可求得BC.
解:∵DE∥BC,
∴DE:BC=AD:AB=1:3,
即6:BC=1:3,
∴BC=18.
故答案为:18.
【点睛】考查相似三角形的判定与性质,掌握相似三角形的性质是解题的关键.
10.【考点】相似三角形的判定
【分析】先判断出两根铝材哪根为边,需截哪根,再根据相似三角形的对应边成比例求出另外两边的长,由另外两边的长的和与另一根铝材相比较即可.
解:∵两根铝材的长分别为27cm,45cm,若45cm为一边时,
则另两边的和为27cm,27<45,不能构成三角形,
∴必须以27cm为一边,45cm的铝材为另外两边,
设另外两边长分别为x,y,则:
若27cm与24cm相对应时,
,
解得:x=33.75cm,y=40.5cm,
x+y=33.75+40.5=74.25cm>45cm,故不成立,
若27cm与36cm相对应时,
,
解得:x=22.5cm,y=18cm,x+y=22.5+18=40.5cm<45cm,成立,
若27cm与30cm相对应时,
, 解得:x=32.4cm,y=21.6cm,x+y=32.4+21.6=54cm>45cm,故不成立,故只有一种截法.
【点睛】本题主要考查相似三角形的性质及三角形成立的条件,解决本题的关键是要根据三角形的边长分情况讨论,利用相似三角形三边对应成比例列式求解.
11.【考点】相似三角形的判定
解:由于∠C=∠E=90°,,根据两角对应相等,两三角形相似得:Rt△ABC∽Rt△ADE.所以:,即:AD=.
故答案:.
12.【考点】相似三角形的判定
解:∵在平行四边形ABCD中,AB=10,AD=6,E是AD的中点,
∴CD=10,BC=6,DE=3.
∵△CBF∽△CDE,
∴BF:DE=BC:DC,
∴BF=6÷10×3=1.8.
13.【考点】相似三角形的判定
【分析】由可得出∠BPM=∠A,进而由等边三角形性质和角的转化可得.
解:∵
∴∠BPM=∠A,
∵是等边三角形
∴∠A+∠APN=60°,∠APN+∠MPN=60°
∴∠APB=∠BPM+∠MPN+∠APN=60°+60=120°.
【点睛】本题考查了相似三角形的性质,熟悉换算是解决本题的关键.
14.【考点】相似三角形的判定
解:∵①中的三角形的三边分别是:2, , ;
②中的三角形的三边分别是:3, , ;
③中的三角形的三边分别是:2,2,2;
④中的三角形的三边分别是:3, ,4;
∵①与③中的三角形的三边的比为:1: :
∴①与③相似.
故答案为:①③.
【点睛】相似三角形的判定方法:(1)平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;
(2)三边法:三组对应边的比相等的两个三角形相似;
(3)两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;
(4)两角法:有两组角对应相等的两个三角形相似.
15.【考点】相似三角形的判定
【分析】此题主要应用两三角形相似的判定定理,三边对应成比例的两个三角形相似,分析作答即可.
解:已知在△ABC中,三条边的长分别为2,3,4,△ 的两边长分别为1,1.5,可以看出,△的两边分别为△ABC的两边长的一半,因此要使△ABC∽△需两三角形各边对应成比例,则第三边长就为4的一半即2.
16.【考点】相似三角形的判定
【分析】先根据三边对应成比例,两三角形相似可判定△ABC∽△DBE,再根据相似三角形对应角相等可得: ∠ABC=∠DBE,然后根据角的和差关系可得∠ABC-∠DBC=∠DBE-∠DBC,继而可证: ∠ABD=∠CBE.
解:∵,
∴△ABC∽△DBE,
∴∠ABC=∠DBE,
∴∠ABC-∠DBC=∠DBE-∠DBC,
即∠ABD=∠CBE.
【点睛】本题主要考查相似三角形的判定和性质,解决本题的关键是要熟练掌握相似三角形的判定和性质.
17.【考点】相似三角形的判定
【分析】先根据勾股定理计算出网格中三角形的各个边长,然后求出各边比值,根据三边对应成比例两三角形相似可得△ABD∽△DCB,然后再可得∠BDC=∠BAD=135°.
解:由图知AB=,AD=1,BD=,BC=5,DC=,
∴,,,
∴,
∴△ABD∽△DCB,
∴∠BDC=∠BAD=135°.
【点睛】本题主要考查相似三角形的判定定理,解决本题的关键是要熟练掌握相似三角形的判定方法.
18.【考点】相似三角形的判定
【分析】根据三边对应成比例的两个三角形相似,可得△ADE∽△CAB,再根据相似三角形的对应角相等可得到∠AED=∠ABC,从而可证AB=AE.
解:∵,
∴△ADE∽△CAB,(三条对应边成比例,两三角形相似),
∴∠AED=∠ABC,
∴AB=AE.
19.【考点】相似三角形的判定
【分析】根据三角形中位线的判定可得:DE,DF,EF,是△ABC的中位线,然后根据中位线的性质可得:,最后根据三边对应成比例,两三角形相似可判定△ABC∽△FDE.
解:∵点D,E,F分别是CA,AB,BC的中点,
∴,
∴△ABC∽△FDE.
【点睛】本题主要考查三角形中位线的判定和性质,相似三角形的判定,解决本题的关键是要熟练掌握中位线的判定和性质,相似三角形的判定.
20.【考点】相似三角形的判定
【分析】由已知可推出两个图形对应角相等,对应边成比例,所以相似.
解:∵∠A=180°-∠B-∠C=82.5°,∠A′=180°-∠B′-∠C′=82.5°,
∴∠A=∠A′,∠B=∠B′,∠C=∠C′.
又∵,,,
∴.
∴根据相似图形的定义可知,△ABC与△A′B′C′相似,相似比是3∶1.
【点睛】本题考核知识点:相似判定. 解题关键点:理解相似的条件.
21.【考点】相似三角形的判定
【分析】(1)、根据,得出△ABC∽△AED,从而说明∠BAC=∠EAD,然后得出答案;(2)、根据得出,结合∠BAE=∠CAD得出三角形相似.
解:(1)∠BAE与∠CAD相等.
在△ABC和△AED中,
∵,
∴△ABC∽△AED,
∴∠BAC=∠EAD,
∴∠BAE=∠CAD;
(2)△ABE与△ACD相似.
由
得,
在△ABE和△ACD中,
∵,
∠BAE=∠CAD,
∴△ABE∽△ACD.
22.【考点】相似三角形的判定
【分析】(1)根据正方形的对角线可得∠ABC的补角等于45°,即可求出∠ABC=135°,根据BC是正方形的对角线,利用勾股定理进行计算即可.
(2)先根据勾股定理计算出网格中三角形的各个边长,然后求出各边比值,根据三边对应成比例两三角形相似可得△ABD∽△DCB,然后再可得
解:(1) 135° 2
(2) 由图知,AB=2,BC=2,AC=2,DF=,EF=2,DE=,
∴,,,
∴,
∴△DEF∽△ACB,
∴∠C=∠E.
【点睛】本题主要考查相似三角形的判定和性质,解决本题的关键是要熟练掌握相似三角形的判定和性质.
23.【考点】相似三角形的判定
【分析】(1)由相似三角形的判定可得△ABC∽△DEF,再根据相似三角形的性质即可解出;(2) 利用边角的关系证出△ABD∽△ACE,从而得出∠ACE+∠ACD=90°,得出结论.
解:(1)∵
∴△ABC∽△DEF???
∴,
(2)∵BAC=DAE??
∴BAD=CAE?
又∵
∴?
∴△ABD∽△ACE?
∴ABD=ACE
∵BAC=90°
∴ABD+ACD=90°?????
∴ACE+ACD=90°?
即ECBC.
【点睛】本题考查了相似三角形的性质与判定,熟练掌握相似三角形的判定是解题的关键.
24.【考点】相似三角形的判定
【分析】由在△ABC和△ADE中,,可证得△ABC∽△ADE,即可证得∠BAD=∠CAE,又由,即可证得:△ABD∽△ACE.
证明:∵在△ABC和△ADE中,,
∴△ABC∽△ADE,
∴∠BAC=∠DAE,
∴∠BAD=∠CAE,
∵,
∴,
∴△ABD∽△ACE.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
