九年级数学24.1圆的有关性质同步提高测试(含答案)
文档属性
| 名称 | 九年级数学24.1圆的有关性质同步提高测试(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 188.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-12 00:00:00 | ||
图片预览



文档简介
九年级数学24.1《圆的有关性质》同步提高测试
一、选择题:
1、下列条件中,可以画出唯一一个圆的是( )
A.已知圆心 B.已知半径
C.已知不在同一直线上的三点 D.已知直径
2、已知⊙0的直径AB=40,弦CD⊥AB于点E,且CD=32,则AE=( )
A.12 B.8 C.12 或28 D.8 或32
3、如图,甲顺着大半圆从A到B地,乙顺着小半圆从A地B到地,设甲、乙走过的路程分别为a、b,则( )
A.a=b B.a > b C.a < b D.不能确定
4、(2018?济宁)如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是( )
A.50° B.60° C.80° D.100°
5、如图,在⊙O中,AE是直径,半径OC垂直于弦AB于D,连接BE,若AB=2,CD=1,则BE的长是( )
A.5 B.6 C.7 D.8
6、下列说法正确的是( )
A.过弦的中点的直径平分弦所对的两条弧
B.弦的垂直平分线平分它所对的两条弧,但不一定过圆心
C.过弦的中点的直径垂直于弦
D.平分弦所对的两条弧的直径平分弦
7、(2018?安顺)已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为( )
A.2cm B.4cm C.2cm或4cm D.2cm或4cm
8、如图,点A、B、C、D在⊙O上,∠AOC=140°,点B是的中点,则∠D的度数是( )
A.70° B.55° C.35.5° D.35°
9、如图,⊙O的半径为5,弦AB=8,M是弦AB上的动点,则OM不可能为( )
A.2 B.3 C.4 D.5
10、(2018?张家界)如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则AE=( )
A.8cm B.5cm C.3cm D.2cm
11、如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2,则该半圆的半径为( )
A.4+√5cm B.9 cm C.4√5cm D.6√2cm
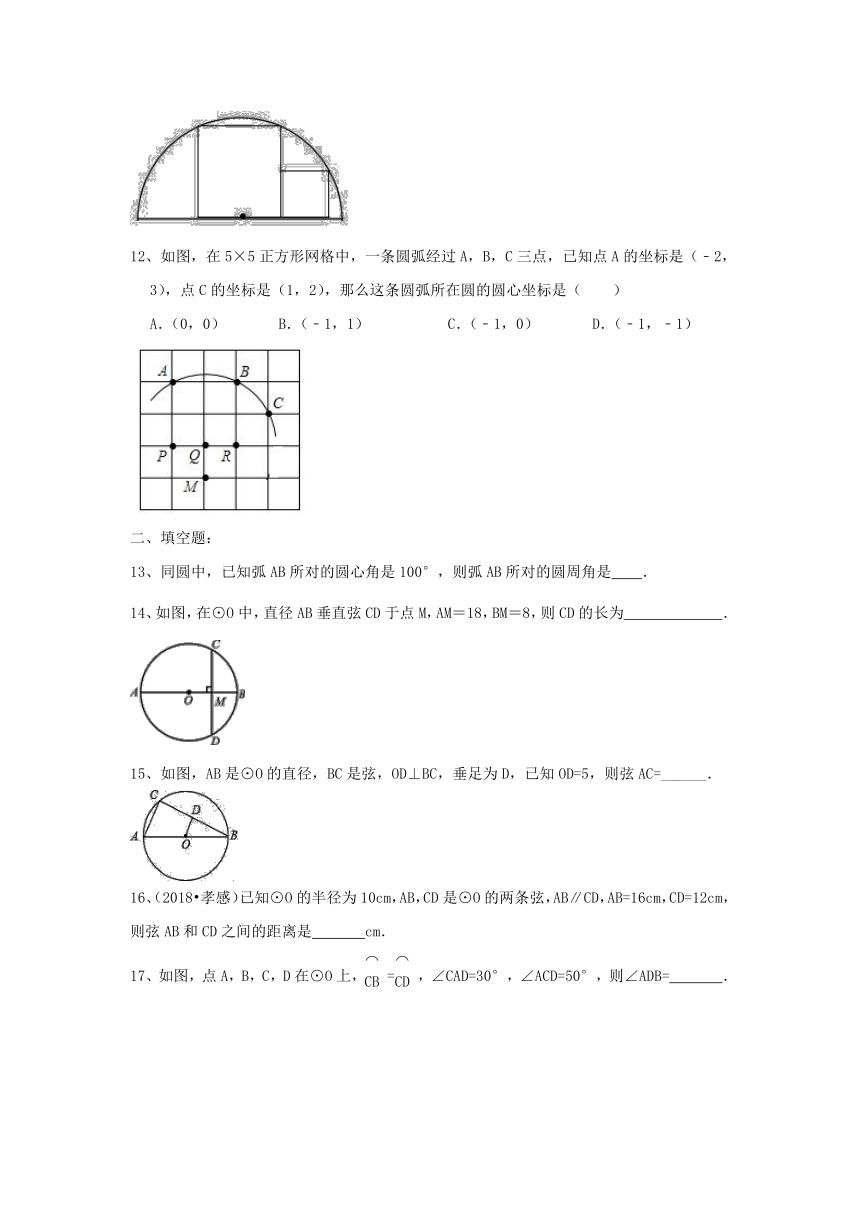
12、如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,已知点A的坐标是(﹣2,3),点C的坐标是(1,2),那么这条圆弧所在圆的圆心坐标是( )
A.(0,0) B.(﹣1,1) C.(﹣1,0) D.(﹣1,﹣1)
二、填空题:
13、同圆中,已知弧AB所对的圆心角是100°,则弧AB所对的圆周角是 .
14、如图,在⊙O中,直径AB垂直弦CD于点M,AM=18,BM=8,则CD的长为?????? .
如图,AB是⊙O的直径,BC是弦,OD⊥BC,垂足为D,已知OD=5,则弦AC=______.
16、(2018?孝感)已知⊙O的半径为10cm,AB,CD是⊙O的两条弦,AB∥CD,AB=16cm,CD=12cm,则弦AB和CD之间的距离是 cm.
17、如图,点A,B,C,D在⊙O上,=,∠CAD=30°,∠ACD=50°,则∠ADB= .
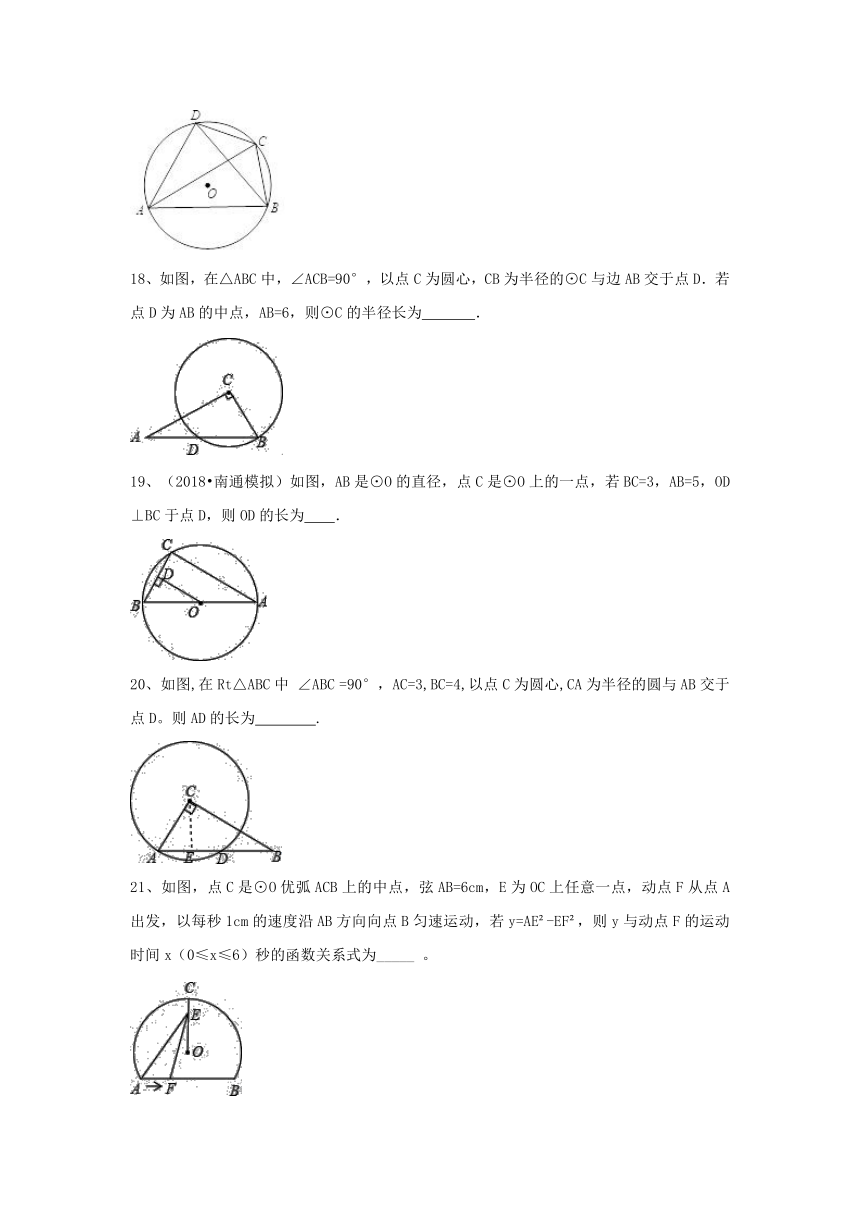
18、如图,在△ABC中,∠ACB=90°,以点C为圆心,CB为半径的⊙C与边AB交于点D.若点D为AB的中点,AB=6,则⊙C的半径长为 .
19、(2018?南通模拟)如图,AB是⊙O的直径,点C是⊙O上的一点,若BC=3,AB=5,OD⊥BC于点D,则OD的长为 .
如图,在Rt△ABC中 ∠ABC =90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D。则AD的长为 .
21、如图,点C是⊙O优弧ACB上的中点,弦AB=6cm,E为OC上任意一点,动点F从点A出发,以每秒1cm的速度沿AB方向向点B匀速运动,若y=AE?-EF?,则y与动点F的运动时间x(0≤x≤6)秒的函数关系式为_____ 。
22、如图,点A,B,C,D在⊙O上, =,∠CAD=30°,∠ACD=50°,则∠ADB= .
三、解答题:
23、如图,AB是⊙O的直径,C、D两点在⊙O上,若∠C=45°,
(1)求∠ABD的度数;
(2)若∠CDB=30°,BC=3,求⊙O的半径.
24、如图,⊙O中,弦CD与直径AB交于点H.
(1)当∠B+∠D=90°时,求证:H是CD的中点;
(2)若H为CD的中点,且CD=2,BD=,求AB的长.
25、如图:⊙O1和⊙O2是等圆,P是O1O2的中点,过P作直线AD交⊙O1于A、B,交⊙O2于C、D,求证:AB=CD.
26、已知如图:D是⊙O劣弧AC的中点,连结AD并延长AD到B,使DB=AD,连结BC并延长交⊙O于E,连结AE,BF⊥AE于F.
(1)求证:AE是⊙O的直径.
(2)若⊙O的半径为4,AD=2,求BF的长.
27、(2018?宜昌)如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.
参考答案:
一、选择题:
1、C
2、D
3、A
4、D
5、B
6、D
7、C
8、D
9、A
10、A
11、C
12、B
二、填空题:
13、50°
14、24
15、10
16、2或14
17、70°
18、3
19、2
20、18/5
21、y=6x-x2
22、70°
三、解答题:
23、(1)∵∠C=45°,∴∠A=∠C=45°,
∵AB是⊙O的直径,∴∠ADB=90°,∴∠ABD=45°;
(2)连接AC,∵AB是⊙O的直径,∴∠ACB=90°,
∵∠CAB=∠CDB=30°,BC=3,∴AB=6,∴⊙O的半径为3.
24、(1)证明:∵∠B+∠D=90°,
∴∠BHD=180°﹣90°=90°,
即AB⊥CD,
∵AB过O,
∴CH=DH,
即H是CD的中点;
(2)解:
连接OD,
∵H为CD的中点,CD=2,AB过O,
∴DH=CH=CD=,AB⊥CD,
∴∠BHD=90°,
由勾股定理得:BH===1,
设⊙O的半径为R,则AB=2R,OB=OD=R,
在Rt△OHD中,由勾股定理得:OH2+DH2=OD2,
即(R﹣1)2+()2=R2,
解得:R=,
∴AB=2×=3.
25、过点O1作O1M⊥AB于M,过点O2作O2N⊥CD于N,
再证明△O1MP≌△O2NP,得OM=ON,∴AB=CD
26、(1)证明:连接DE,
∵D是⊙O劣弧AC的中点,
∴=,
∴∠AED=∠BED,
∵DB=AD,
∴DE⊥AB,
∴AE是⊙O的直径.
(2)∵由(1)知AE是⊙O的直径,
∴∠ADE=90°.
∵⊙O的半径为4,AD=2,
∴AE=8,
∴DE==2.
∵DB=AD,
∴AB=2AD=4.
∵BF⊥AE于F,
∴BF===.
27、(1)证明:∵AB是直径,
∴∠AEB=90°,
∴AE⊥BC,
∵AB=AC,
∴BE=CE,
∵AE=EF,
∴四边形ABFC是平行四边形,
∵AC=AB,
∴四边形ABFC是菱形.
(2)设CD=x.连接BD.
∵AB是直径,
∴∠ADB=∠BDC=90°,
∴AB2﹣AD2=CB2﹣CD2,
∴(7+x)2﹣72=42﹣x2,
解得x=1或﹣8(舍弃)
∴AC=8,BD==,
∴S菱形ABFC=8.
∴S半圆=?π?42=8π.
一、选择题:
1、下列条件中,可以画出唯一一个圆的是( )
A.已知圆心 B.已知半径
C.已知不在同一直线上的三点 D.已知直径
2、已知⊙0的直径AB=40,弦CD⊥AB于点E,且CD=32,则AE=( )
A.12 B.8 C.12 或28 D.8 或32
3、如图,甲顺着大半圆从A到B地,乙顺着小半圆从A地B到地,设甲、乙走过的路程分别为a、b,则( )
A.a=b B.a > b C.a < b D.不能确定
4、(2018?济宁)如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是( )
A.50° B.60° C.80° D.100°
5、如图,在⊙O中,AE是直径,半径OC垂直于弦AB于D,连接BE,若AB=2,CD=1,则BE的长是( )
A.5 B.6 C.7 D.8
6、下列说法正确的是( )
A.过弦的中点的直径平分弦所对的两条弧
B.弦的垂直平分线平分它所对的两条弧,但不一定过圆心
C.过弦的中点的直径垂直于弦
D.平分弦所对的两条弧的直径平分弦
7、(2018?安顺)已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为( )
A.2cm B.4cm C.2cm或4cm D.2cm或4cm
8、如图,点A、B、C、D在⊙O上,∠AOC=140°,点B是的中点,则∠D的度数是( )
A.70° B.55° C.35.5° D.35°
9、如图,⊙O的半径为5,弦AB=8,M是弦AB上的动点,则OM不可能为( )
A.2 B.3 C.4 D.5
10、(2018?张家界)如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则AE=( )
A.8cm B.5cm C.3cm D.2cm
11、如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2,则该半圆的半径为( )
A.4+√5cm B.9 cm C.4√5cm D.6√2cm
12、如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,已知点A的坐标是(﹣2,3),点C的坐标是(1,2),那么这条圆弧所在圆的圆心坐标是( )
A.(0,0) B.(﹣1,1) C.(﹣1,0) D.(﹣1,﹣1)
二、填空题:
13、同圆中,已知弧AB所对的圆心角是100°,则弧AB所对的圆周角是 .
14、如图,在⊙O中,直径AB垂直弦CD于点M,AM=18,BM=8,则CD的长为?????? .
如图,AB是⊙O的直径,BC是弦,OD⊥BC,垂足为D,已知OD=5,则弦AC=______.
16、(2018?孝感)已知⊙O的半径为10cm,AB,CD是⊙O的两条弦,AB∥CD,AB=16cm,CD=12cm,则弦AB和CD之间的距离是 cm.
17、如图,点A,B,C,D在⊙O上,=,∠CAD=30°,∠ACD=50°,则∠ADB= .
18、如图,在△ABC中,∠ACB=90°,以点C为圆心,CB为半径的⊙C与边AB交于点D.若点D为AB的中点,AB=6,则⊙C的半径长为 .
19、(2018?南通模拟)如图,AB是⊙O的直径,点C是⊙O上的一点,若BC=3,AB=5,OD⊥BC于点D,则OD的长为 .
如图,在Rt△ABC中 ∠ABC =90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D。则AD的长为 .
21、如图,点C是⊙O优弧ACB上的中点,弦AB=6cm,E为OC上任意一点,动点F从点A出发,以每秒1cm的速度沿AB方向向点B匀速运动,若y=AE?-EF?,则y与动点F的运动时间x(0≤x≤6)秒的函数关系式为_____ 。
22、如图,点A,B,C,D在⊙O上, =,∠CAD=30°,∠ACD=50°,则∠ADB= .
三、解答题:
23、如图,AB是⊙O的直径,C、D两点在⊙O上,若∠C=45°,
(1)求∠ABD的度数;
(2)若∠CDB=30°,BC=3,求⊙O的半径.
24、如图,⊙O中,弦CD与直径AB交于点H.
(1)当∠B+∠D=90°时,求证:H是CD的中点;
(2)若H为CD的中点,且CD=2,BD=,求AB的长.
25、如图:⊙O1和⊙O2是等圆,P是O1O2的中点,过P作直线AD交⊙O1于A、B,交⊙O2于C、D,求证:AB=CD.
26、已知如图:D是⊙O劣弧AC的中点,连结AD并延长AD到B,使DB=AD,连结BC并延长交⊙O于E,连结AE,BF⊥AE于F.
(1)求证:AE是⊙O的直径.
(2)若⊙O的半径为4,AD=2,求BF的长.
27、(2018?宜昌)如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.
参考答案:
一、选择题:
1、C
2、D
3、A
4、D
5、B
6、D
7、C
8、D
9、A
10、A
11、C
12、B
二、填空题:
13、50°
14、24
15、10
16、2或14
17、70°
18、3
19、2
20、18/5
21、y=6x-x2
22、70°
三、解答题:
23、(1)∵∠C=45°,∴∠A=∠C=45°,
∵AB是⊙O的直径,∴∠ADB=90°,∴∠ABD=45°;
(2)连接AC,∵AB是⊙O的直径,∴∠ACB=90°,
∵∠CAB=∠CDB=30°,BC=3,∴AB=6,∴⊙O的半径为3.
24、(1)证明:∵∠B+∠D=90°,
∴∠BHD=180°﹣90°=90°,
即AB⊥CD,
∵AB过O,
∴CH=DH,
即H是CD的中点;
(2)解:
连接OD,
∵H为CD的中点,CD=2,AB过O,
∴DH=CH=CD=,AB⊥CD,
∴∠BHD=90°,
由勾股定理得:BH===1,
设⊙O的半径为R,则AB=2R,OB=OD=R,
在Rt△OHD中,由勾股定理得:OH2+DH2=OD2,
即(R﹣1)2+()2=R2,
解得:R=,
∴AB=2×=3.
25、过点O1作O1M⊥AB于M,过点O2作O2N⊥CD于N,
再证明△O1MP≌△O2NP,得OM=ON,∴AB=CD
26、(1)证明:连接DE,
∵D是⊙O劣弧AC的中点,
∴=,
∴∠AED=∠BED,
∵DB=AD,
∴DE⊥AB,
∴AE是⊙O的直径.
(2)∵由(1)知AE是⊙O的直径,
∴∠ADE=90°.
∵⊙O的半径为4,AD=2,
∴AE=8,
∴DE==2.
∵DB=AD,
∴AB=2AD=4.
∵BF⊥AE于F,
∴BF===.
27、(1)证明:∵AB是直径,
∴∠AEB=90°,
∴AE⊥BC,
∵AB=AC,
∴BE=CE,
∵AE=EF,
∴四边形ABFC是平行四边形,
∵AC=AB,
∴四边形ABFC是菱形.
(2)设CD=x.连接BD.
∵AB是直径,
∴∠ADB=∠BDC=90°,
∴AB2﹣AD2=CB2﹣CD2,
∴(7+x)2﹣72=42﹣x2,
解得x=1或﹣8(舍弃)
∴AC=8,BD==,
∴S菱形ABFC=8.
∴S半圆=?π?42=8π.
同课章节目录
