上海市浦东新区第四教育署2019届九年级(五四学制)上学期期中考试数学试题(含答案)
文档属性
| 名称 | 上海市浦东新区第四教育署2019届九年级(五四学制)上学期期中考试数学试题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 237.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-12 00:00:00 | ||
图片预览



文档简介
九年级数学学科阶段练习(2018.11)
(时间:100分钟 满分:100分)
一、选择题:(本大题共6题,每题4分,满分24分)
1.若ac=bd(ac≠0),则下列比例式中不成立的是( )
A. B. C. D.
2.已知:Rt△ABC中,∠C=90°,sinB=,则tanA等于( )
A. B. C. D.
3.如果点D、E分别在△ABC的两边AB、AC上,下列条件中可以推出DE∥BC的是( )
A.=,= B.=,= C.=,= D.=,=
4.把△ABC的各边长都增加两倍,则锐角A的正弦值 ( )
A.增加2倍 B.增加4倍 C.不变 D.不能确定
5.已知线段a、b、c,求作线段x,使,以下做法正确的是…( )
6. 如图,∠ABC=∠CDB=90°,BC=3,AC=5,如果△ABC与△CDB相似,那么BD的长( )
A. B. C. D.或
二、填空题:(本大题共12题,每题4分,满分48分)
7.计算:=_______;
8.在Rt△ABC中,∠A=90°,BC=10,cosB=,AC=__________.
9.已知,AB=4,P是AB黄金分割点,PA>PB,则PA的长为__________.
10.如图,l1∥l2∥l3,AB=4,DF=8,BC=6,则DE=__________.
11.如图,DE∥BC,DF=2,FC=4,那么=__________.
12.如果在比例尺为1︰1 000 000的地图上,A、B两地的图上距离是3.4厘米,那么A、B两地的实际距离是 千米.
13.如果两个相似三角形的面积之比是9∶25,其中小三角形一边上的中线长是12cm,那么大三角形对应边上的中线长是 cm.
14.已知△ABC中,点D在边BC上,且BD=2DC.设,,那么等于
__________________ (结果用、表示);
15.如图,若点G是△ABC的重心,GD∥BC,则=__________.
16.如图,正△ABC中,P为BC上一点,D为AC上一点,∠APD=60°,BP=1,CD=,则△ABC的边长为______
17. 如图,Rt△ABC中,∠C=90°,BC=4,AC=6,现将△ABC沿ED翻折,使点A与点B重合,折痕为DE,则tan∠BED的值是__________. ____.
18.如图,在△ABC中,∠C=90°,AB=10,cosB=,点M是AB边的中点,将△ABC绕着点M旋转,使点C与点A重合,点A与点D重合,点B与点E重合,得到△DEA,且AE交CB于点P,那么线段CP的长是__________.
三、解答题:(本大题共7题,满分78分)
19.(10分)计算:
20.(10分)如图,在△ABC中,点D在边AB上,点F、E在边AC上,且DF∥BE,.
求:的值.
21.如图,在△ABC中,AB=AC,BD是AC边上的中线,AE⊥BC,垂足为点E,交BD于F,cos∠ABC=,AB=13.
(1)求AE的长;(5分)
(2)求tan∠DBC的值.(5分)
22.如图:四边形ABCD对角线AC与BD相交于点O,OD=2OA,OC=2OB.
(1)求证:△AOB∽△DOC;(5分)
(2)点E在线段OC上,若AB∥DE,求证:OD2=OE?OC.(5分)
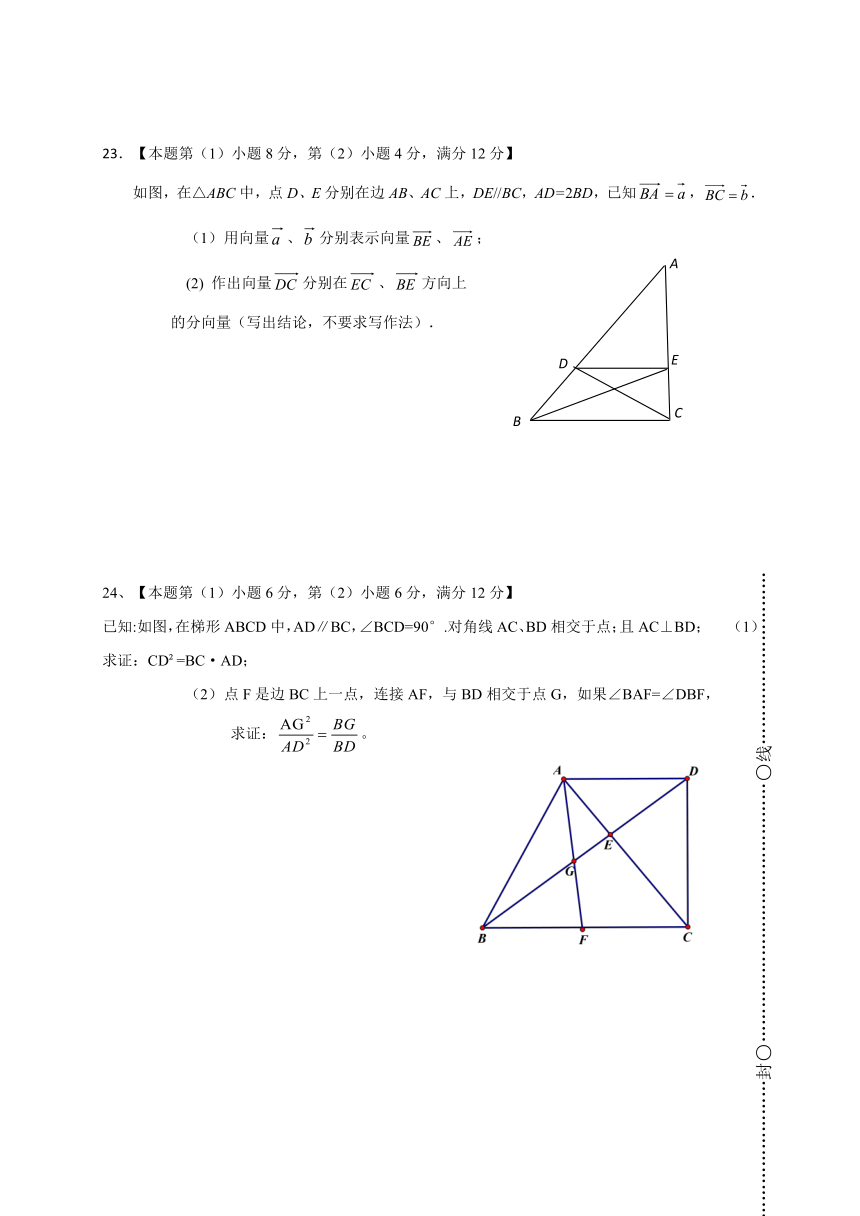
23.【本题第(1)小题8分,第(2)小题4分,满分12分】
如图,在△ABC中,点D、E分别在边AB、AC上,DE//BC,AD=2BD,已知,.
用向量、分别表示向量、;
作出向量分别在、方向上
的分向量(写出结论,不要求写作法).
24、【本题第(1)小题6分,第(2)小题6分,满分12分】
已知:如图,在梯形ABCD中,AD∥BC,∠BCD=90°.对角线AC、BD相交于点;且AC⊥BD; (1)求证:CD2=BC·AD;
点F是边BC上一点,连接AF,与BD相交于点G,如果∠BAF=∠DBF,
求证:。
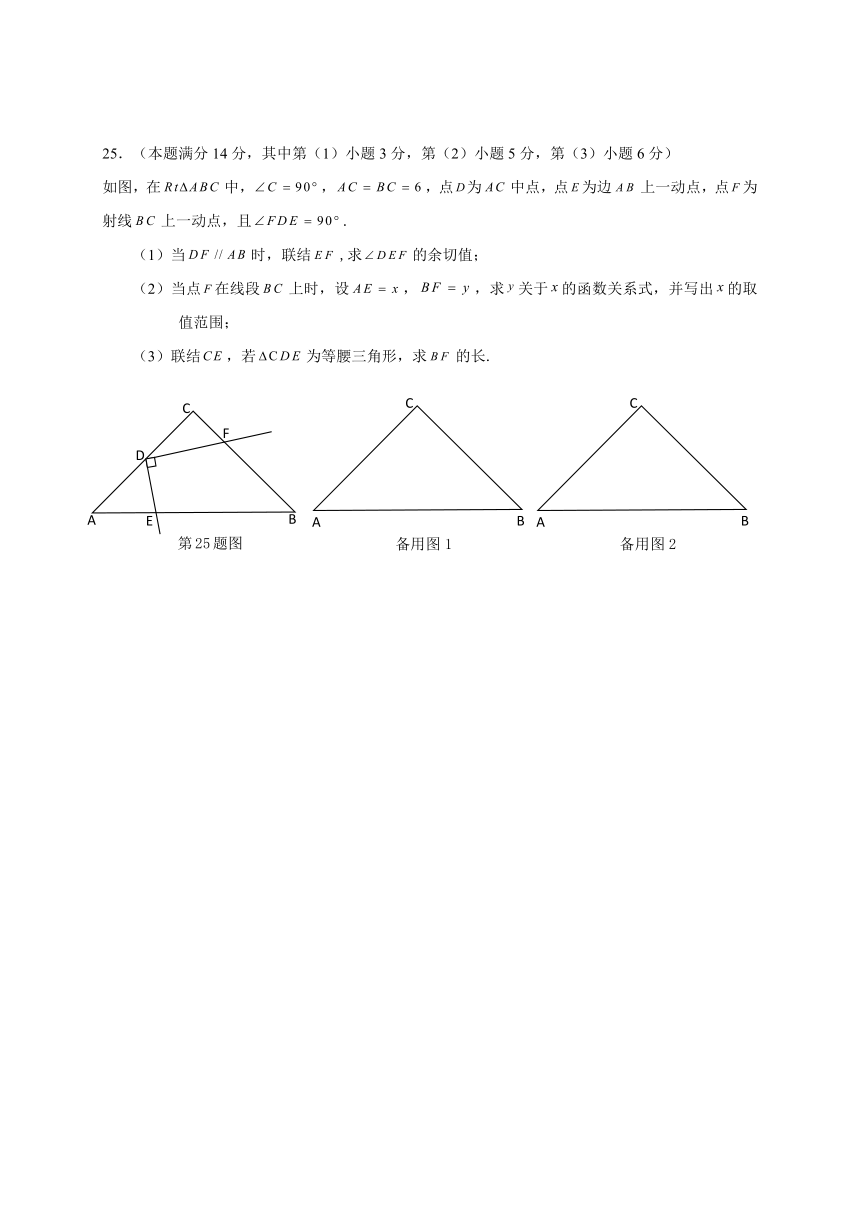
25.(本题满分14分,其中第(1)小题3分,第(2)小题5分,第(3)小题6分)
如图,在中,,,点为中点,点为边上一动点,点为射线上一动点,且.
(1)当时,联结,求的余切值;
(2)当点在线段上时,设,,求关于的函数关系式,并写出的取值范围;
(3)联结,若为等腰三角形,求的长.
九年级数学学科阶段练习(2018.11)参考答案
1、C;2、D;3、C;4、C;5、C;6、D.
7、3-2 8、8; 9、;10、; 11、1; 12、34;13、20
14、 ;15、;16、3;17、;18、
19、 ……………………………(4分)
=……………………………(4分)
=……………………………(2分)
DF∥BE
………………………(2分)
....................(2分)
............ ......(2分)
.....................(2分)
........................(2分)
21、
23解:(1)∵DE//BC,AD=2BD,∴,∴,…(2分)
∵与方向相同,∴,…………………(2分)
∵,∴.……………………(2分)
∵,∴.…………………(2分)
(2)作出的图形中,分别在、方向上的分向量并说明.…(各2分)
说明:第(1)题可用不同做法形式,同样分步给分,第(2)题只要大小方向正确,与位置无关.
24、证明:(1)∵AD//BC,∠BCD=90o,∴∠ADC=∠BCD=90o.……………(1分)
又∵AC⊥BD,∴∠ACD+∠ACB=∠CBD+∠ACB=90o.……………………(1分)
∴∠ACD=∠CBD. …………………………………………………………(1分)
∴△ACD∽△DBC.…………………………………………………………(2分)
∴,即.…………………………………………(1分)
(2)∵AD//BC,∴∠ADB=∠DBF.
∵∠BAF=∠DBF,∴∠ADB=∠BAF.…………………………………(1分)
∵∠ABG=∠DBA,∴△ABG∽△DBA. …………………………………(1分)
∴.………………………………………………………………(1分)
∴.
又由于△ABG∽△DBA,∴.………………………………(1分)
∴.………………………………………………………(1分)
∴.…………………………………………(1分)
另证:∵AD//BC,∠ADB=∠DBF.
∵∠BAF=∠DBF,∴∠ADB=∠BAF.…………………………………(1分)
∵∠ABG=∠DBA,∴△ABG∽△DBA. ……………………………………(1分)
∴. …………………………………………………(2分)
而,∴.…………………………………………(2分)
25、解:(1)∴,∠°
∴
∵∥,
∴……………………………………………………(1分)
∴…………………………………………………………………(1分)
在中,…………………………(2分)
(2)过点作于点
可求得……………………(1分)
∴
又可证∽
∴………………………………………………………………(1分)
∴
∴()…………………………………………(2分,1分)
(3)∵, ∴
∴若为等腰三角形,只有或两种可能.…………(1分)
当时,点在边上,
过点作⊥于点(如图①)
可得:,
即点在中点
∴此时与重合 ∴……………………(2分)
当时,点在的延长线上,
过点作⊥于点(如图②)
可证: △∽△
∴
∴
∴ ∴ ……………………………(2分)
综上所述,为6或7.
(时间:100分钟 满分:100分)
一、选择题:(本大题共6题,每题4分,满分24分)
1.若ac=bd(ac≠0),则下列比例式中不成立的是( )
A. B. C. D.
2.已知:Rt△ABC中,∠C=90°,sinB=,则tanA等于( )
A. B. C. D.
3.如果点D、E分别在△ABC的两边AB、AC上,下列条件中可以推出DE∥BC的是( )
A.=,= B.=,= C.=,= D.=,=
4.把△ABC的各边长都增加两倍,则锐角A的正弦值 ( )
A.增加2倍 B.增加4倍 C.不变 D.不能确定
5.已知线段a、b、c,求作线段x,使,以下做法正确的是…( )
6. 如图,∠ABC=∠CDB=90°,BC=3,AC=5,如果△ABC与△CDB相似,那么BD的长( )
A. B. C. D.或
二、填空题:(本大题共12题,每题4分,满分48分)
7.计算:=_______;
8.在Rt△ABC中,∠A=90°,BC=10,cosB=,AC=__________.
9.已知,AB=4,P是AB黄金分割点,PA>PB,则PA的长为__________.
10.如图,l1∥l2∥l3,AB=4,DF=8,BC=6,则DE=__________.
11.如图,DE∥BC,DF=2,FC=4,那么=__________.
12.如果在比例尺为1︰1 000 000的地图上,A、B两地的图上距离是3.4厘米,那么A、B两地的实际距离是 千米.
13.如果两个相似三角形的面积之比是9∶25,其中小三角形一边上的中线长是12cm,那么大三角形对应边上的中线长是 cm.
14.已知△ABC中,点D在边BC上,且BD=2DC.设,,那么等于
__________________ (结果用、表示);
15.如图,若点G是△ABC的重心,GD∥BC,则=__________.
16.如图,正△ABC中,P为BC上一点,D为AC上一点,∠APD=60°,BP=1,CD=,则△ABC的边长为______
17. 如图,Rt△ABC中,∠C=90°,BC=4,AC=6,现将△ABC沿ED翻折,使点A与点B重合,折痕为DE,则tan∠BED的值是__________. ____.
18.如图,在△ABC中,∠C=90°,AB=10,cosB=,点M是AB边的中点,将△ABC绕着点M旋转,使点C与点A重合,点A与点D重合,点B与点E重合,得到△DEA,且AE交CB于点P,那么线段CP的长是__________.
三、解答题:(本大题共7题,满分78分)
19.(10分)计算:
20.(10分)如图,在△ABC中,点D在边AB上,点F、E在边AC上,且DF∥BE,.
求:的值.
21.如图,在△ABC中,AB=AC,BD是AC边上的中线,AE⊥BC,垂足为点E,交BD于F,cos∠ABC=,AB=13.
(1)求AE的长;(5分)
(2)求tan∠DBC的值.(5分)
22.如图:四边形ABCD对角线AC与BD相交于点O,OD=2OA,OC=2OB.
(1)求证:△AOB∽△DOC;(5分)
(2)点E在线段OC上,若AB∥DE,求证:OD2=OE?OC.(5分)
23.【本题第(1)小题8分,第(2)小题4分,满分12分】
如图,在△ABC中,点D、E分别在边AB、AC上,DE//BC,AD=2BD,已知,.
用向量、分别表示向量、;
作出向量分别在、方向上
的分向量(写出结论,不要求写作法).
24、【本题第(1)小题6分,第(2)小题6分,满分12分】
已知:如图,在梯形ABCD中,AD∥BC,∠BCD=90°.对角线AC、BD相交于点;且AC⊥BD; (1)求证:CD2=BC·AD;
点F是边BC上一点,连接AF,与BD相交于点G,如果∠BAF=∠DBF,
求证:。
25.(本题满分14分,其中第(1)小题3分,第(2)小题5分,第(3)小题6分)
如图,在中,,,点为中点,点为边上一动点,点为射线上一动点,且.
(1)当时,联结,求的余切值;
(2)当点在线段上时,设,,求关于的函数关系式,并写出的取值范围;
(3)联结,若为等腰三角形,求的长.
九年级数学学科阶段练习(2018.11)参考答案
1、C;2、D;3、C;4、C;5、C;6、D.
7、3-2 8、8; 9、;10、; 11、1; 12、34;13、20
14、 ;15、;16、3;17、;18、
19、 ……………………………(4分)
=……………………………(4分)
=……………………………(2分)
DF∥BE
………………………(2分)
....................(2分)
............ ......(2分)
.....................(2分)
........................(2分)
21、
23解:(1)∵DE//BC,AD=2BD,∴,∴,…(2分)
∵与方向相同,∴,…………………(2分)
∵,∴.……………………(2分)
∵,∴.…………………(2分)
(2)作出的图形中,分别在、方向上的分向量并说明.…(各2分)
说明:第(1)题可用不同做法形式,同样分步给分,第(2)题只要大小方向正确,与位置无关.
24、证明:(1)∵AD//BC,∠BCD=90o,∴∠ADC=∠BCD=90o.……………(1分)
又∵AC⊥BD,∴∠ACD+∠ACB=∠CBD+∠ACB=90o.……………………(1分)
∴∠ACD=∠CBD. …………………………………………………………(1分)
∴△ACD∽△DBC.…………………………………………………………(2分)
∴,即.…………………………………………(1分)
(2)∵AD//BC,∴∠ADB=∠DBF.
∵∠BAF=∠DBF,∴∠ADB=∠BAF.…………………………………(1分)
∵∠ABG=∠DBA,∴△ABG∽△DBA. …………………………………(1分)
∴.………………………………………………………………(1分)
∴.
又由于△ABG∽△DBA,∴.………………………………(1分)
∴.………………………………………………………(1分)
∴.…………………………………………(1分)
另证:∵AD//BC,∠ADB=∠DBF.
∵∠BAF=∠DBF,∴∠ADB=∠BAF.…………………………………(1分)
∵∠ABG=∠DBA,∴△ABG∽△DBA. ……………………………………(1分)
∴. …………………………………………………(2分)
而,∴.…………………………………………(2分)
25、解:(1)∴,∠°
∴
∵∥,
∴……………………………………………………(1分)
∴…………………………………………………………………(1分)
在中,…………………………(2分)
(2)过点作于点
可求得……………………(1分)
∴
又可证∽
∴………………………………………………………………(1分)
∴
∴()…………………………………………(2分,1分)
(3)∵, ∴
∴若为等腰三角形,只有或两种可能.…………(1分)
当时,点在边上,
过点作⊥于点(如图①)
可得:,
即点在中点
∴此时与重合 ∴……………………(2分)
当时,点在的延长线上,
过点作⊥于点(如图②)
可证: △∽△
∴
∴
∴ ∴ ……………………………(2分)
综上所述,为6或7.
同课章节目录
