《积的变化规律》教学设计
图片预览


文档简介
《积的变化规律》教学设计
【教学内容】
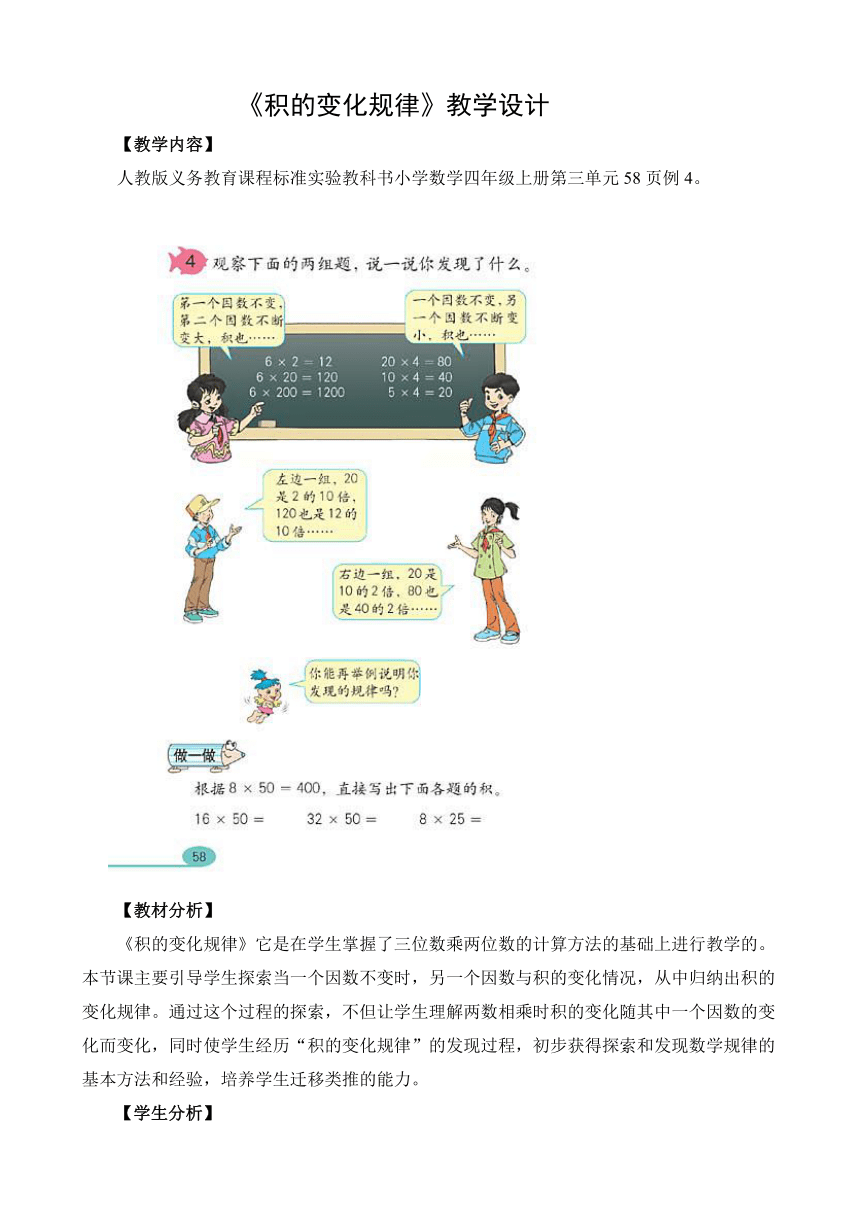
人教版义务教育课程标准实验教科书小学数学四年级上册第三单元58页例4。
【教材分析】
《积的变化规律》它是在学生掌握了三位数乘两位数的计算方法的基础上进行教学的。本节课主要引导学生探索当一个因数不变时,另一个因数与积的变化情况,从中归纳出积的变化规律。通过这个过程的探索,不但让学生理解两数相乘时积的变化随其中一个因数的变化而变化,同时使学生经历“积的变化规律”的发现过程,初步获得探索和发现数学规律的基本方法和经验,培养学生迁移类推的能力。
【学生分析】
学生在前段时间刚完成了数与代数领域中的三位数乘两位数的学习。乘法算式中的规律学习是学生第一次接触,这对于学习纯计算问题有着较大的不同,但又有内在的联系。所以运用新的教学手法来调动学生学习本节课的内容是非常必要的。
【设计理念】
本节课,尝试把数与形结合起来学习“积的变化规律”。使只能靠学生想象、推理的纯代数问题转变为可看、可想的空间与图形的问题。把静态的数与数之间的关系转变成为了动态的变化过程,使学生经历通过长与宽的变化促使图形面积变化的过程。形象、生动,更能唤起学生对知识的渴求。整一节课都围绕这一个中心,就是让学生通过图形面积大小的变化来掌握“积的变化规律”,而又把所掌握的规律应用在解决实际问题上。
【教学目标】
1、把数与形结合起来,让学生经历“积的变化规律”整个过程。
2、培养学生用自己的语言来概括“积的变化规律”。
3、运用知识解决实际问题。
4、培养学生主动探究、合作交流和归纳总结的能力,初步养成严谨的治学态度。
【教学重点】
通过数形结合,引导学生自已发现规律、概括规律,进而运用规律。
【教学难点】
把规律运用在实际问题上。
【教学过程】
一、情景导入,初建数模
1、创设情景,引起悬念
课件出示一个长方形,求面积。(课件演示,第一步:出现一个长方形;第二步:里面出现小正方形;第三步:出现长与宽。)
图1:
师:同学们看,这里每个正方形的面积是1平方厘米。长方形的长10厘米表示什么?宽2厘米表示什么?
引导学生说出:长方形的长是10厘米,表示每一行有10小正方形。宽是2厘米,表示这样的小正方形有2行。
师:这个长方形的面积如何算出?表示什么?
引导学生说出:每行有10个小正方形,有2行,10×2=20,一共有20个小正方形,每个小正方形的面积是1平方厘米,就是20平方厘米。
师:老师想把这个长方形的面积变大,你有什么办法?(预设答案:①把长扩大;②把宽扩大;③把长和宽同时扩大。)
师:同学们想的办法都很好,老师决定先采取把宽扩大的方法使这个长方形的面积变大。
2、直观图形面积的变化
长方形的宽扩大2、3、4倍,面积随着变化。
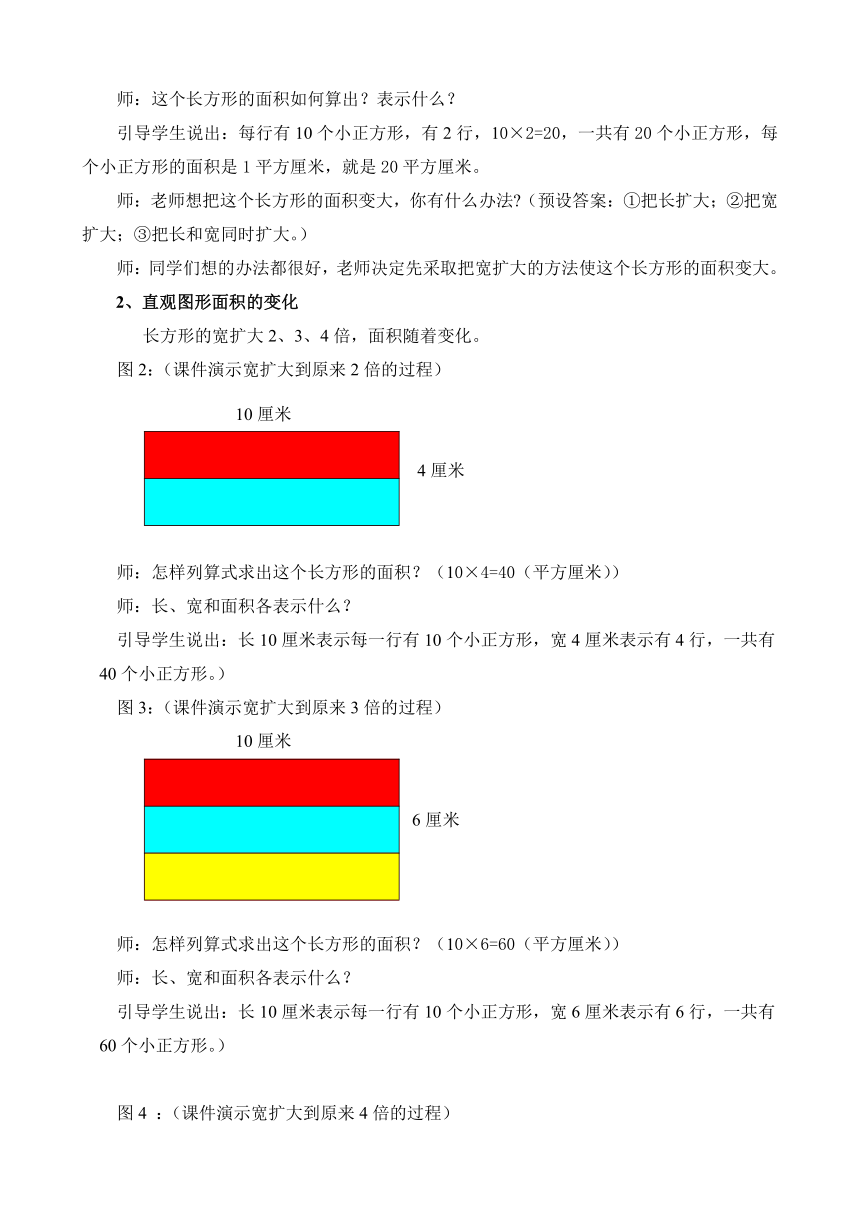
图2:(课件演示宽扩大到原来2倍的过程)
师:怎样列算式求出这个长方形的面积?(10×4=40(平方厘米))
师:长、宽和面积各表示什么?
引导学生说出:长10厘米表示每一行有10个小正方形,宽4厘米表示有4行,一共有40个小正方形。)
图3:(课件演示宽扩大到原来3倍的过程)
师:怎样列算式求出这个长方形的面积?(10×6=60(平方厘米))
师:长、宽和面积各表示什么?
引导学生说出:长10厘米表示每一行有10个小正方形,宽6厘米表示有6行,一共有60个小正方形。)
图4 :(课件演示宽扩大到原来4倍的过程)
师:怎样列算式求出这个长方形的面积?(10×8=80(平方厘米))
师:长、宽和面积各表示什么?
引导学生说出:长10厘米表示每一行有10个小正方形,宽8厘米表示有8行,一共有80个小正方形。)
【设计意图:本环节尝试把数与形结合起来,通过图形面积的变化,使学生能用肉眼看到其中的一个因数变化,使积有所变化的动态演变过程全程显现在学生的面前。借助于“形”的变化,为往后的寻找规律环节做好充分的准备,扫清了学习障碍。】
二、研究问题,寻找规律
1、探索面积随宽的变化而变化的规律
(1)小组讨论
师:先从图1 图4这样顺序观察这四个长方形,什么变了?什么没变?怎么变?再从图4 图1观察,什么变了?什么没变?你能从中找到规律吗?
(学生讨论)
引导学生从上往下对黑板上的式子进行观察、讨论,发现规律。
(1)10×2=20(平方厘米)
(2)10×4=40(平方厘米)
(3)10×6=60(平方厘米)
(4)10×8=80(平方厘米)
(2)汇报交流
(画箭头↓)(穿插课件,出示图形提醒)
引导学生说出:长方形的长不变,宽变了,宽乘2、乘3、乘4……,面积也随着乘2、乘3、乘4……;长不变,宽除以2、除以3、除以4……,面积也会随着除以2、除以3、除以4……。
【设计意图:通过把图形的不断变化随之带来的视觉效果让学生真正感受到“积的变化规律”,有了图形的帮助,使得寻找规律的思路敞开了。学生也能跟着老师一步一个脚印的、扎实的发现并掌握规律。比起单纯的数字游戏活动,印象更深刻更有效果。】
2、探索宽不变,长变化引起面积变化的规律
师:长方形的长不变,宽变化引起了面积的变化。同学们猜想一下,假如长方形的宽不变,长乘2、乘3、乘4……或除以2、除以3、除以4……,也会引起面积有同样的变化吗?
小组讨论,你能以图1来举例说明吗?
预设学生会举例子如:
根据学生的回答,老师列算式。
师:你能根据算式来说说变化的规律吗?
引导学生说出:宽不变,长乘2、乘3、乘4…或长除以2、除以3、除以4……,面积也会跟着乘2、乘3、乘4(或除以2、除以3、除以4……)
【设计意图:通过让学生大胆的猜想,大胆举例来验证长方形的宽不变,长变化了同样也能引起面积的变化规律。使学生在此环节中充分运用自己的经验来解决问题,做到举一反三,并且使学生有自己获取知识的成功感。通过长的变化而引起长方形面积的变化,又是一次视觉的冲击。学生借助图形的变化,会很快找出相应的变化规律。而且在老师的指导下能用比较准确的语言来描述与概括。】
3、整体概括规律
师:在乘法的算式中,乘号前后两个数称为因数。你能把以上所有的算式变化规律用一句话来概括吗?
引导学生用简明的语言表示出来:两数相乘,一个因数不变,另一个因数乘(或除以)几(0除外),积也要乘(或除以)几。(板书规律)并揭示课题:积的变化规律。
三、运用规律,解决问题
师:同学们,从你们刚才的表现老师知道,你们已经学会了“积的变化规律”,但我们不光要掌握它,更重要的是学以致用。
1、基础练习
(1)根据8×50=400,直接写出下面各题的积。(课本P58做一做)
16×50= 32×50= 8×25=
(2)根据7×30=210,直接写出下面各题的得数。
14×30= 21×30= 28×30=
7×60= 7×10= 90×7=
【设计意图:此两个练习主要是围绕着其中一个因数不变,另一个因数乘或除以一个数而展开的。主要的目的是巩固刚刚所寻找到的“积的变化规律”,为下面两个因数的变化而引起积的变化奠定基础,也能从侧面来检查学生对最基本的知识掌握的情况。以此为根据来决定下一个环节的开展程度。】
2、综合练习
师:我们刚刚学会了跟路程有关系的公式:速度×时间=路程。其实,在这公式当中,蕴含着我们本节课的知识在里面,不信你们瞧一瞧!
(根据学生的回答,出现表内黑色字体的数据。)
表一:速度、时间、路程
速度
时间 2小时 4小时 6小时
路程 160千米 320千米 480千米
速度
时间 3小时 3小时 3小时
路程 240千米 480千米 2400千米
师:你能根据以上两个表总结出速度、时间与路程之间的变化规律吗?
引导学生说出在速度不变的情况下,时间乘2、乘3、乘4(或除以2、除以3、除以4……),路程也会乘2、乘3、乘4(或除以2、除以3、除以4……)。反之在时间不变的情况下,速度乘2、乘10(或除以2、除以10)路程也会跟着乘2、乘10(或除以2、除以10)。
表二:单价、数量和总价
师:你能根据(表一)来自己设计“积的变化规律”的数据吗?
单价(元) 数量(本……) 总价(元)
【设计意图:把刚学到的“积的变化规律”马上运用在实际当中。不仅让学生明白到速度、时间与路程三者之间有着怎样紧密的联系,而且也感受到数学知识之间并不是孤立的,知识与知识之间是互相影响着的。学习了的公理或公式都是为了以后的知识学习打基础的。把速度、时间、路程与之联系,极大程度上提高了学生运用知识的能力,也把知识串联起来了。】
3、拓展练习(课本P59第2题)
下面这块长方形绿地的宽要增加到24米,长不变。扩大后的绿地面积是多少?
引导学生利用那个本节课所学到的“积的变化规律”来解决本题。
【设计意图:在新授的同时穿插相关的练习,使学生掌握得更牢固,也加深了印象。我们知道孩子的瞬间记忆是非常强的,假如我们能加以运用,肯定会达到事半功倍的效果。所以整一个环节,都采取了边讲边练的形式。】
四、拓展升华,继续探索
(这部分内容作为弹性要求,视学生学习情况决定是否出现)
1、探索两个因数同时扩大(或缩小),积的变化规律
课件演示长方形从原来的10厘米,宽2厘米。长乘2、宽也乘2,面积的变化。
原来的长方形:
面积是:10×2=20 (平方厘米)
变为:
面积是:(10×2)×(2×2)=80(平方厘米)
师:把长方形的长和宽同时乘2 ,这个长方形的面积会如何变化?为什么?(面积会扩大4倍。因为长乘以2,宽也乘以2,一共乘了4,所以面积也要乘以4.)
(引申规律:一个因数乘以一个数,另一个因数乘以另一个数,积就乘这两个数的积。)
【设计意图:这是“积的变化规律”的又一次升华。引导学生探究当两个因数都发生变化时,积是如何变化的。目的是让学生能跳出书本的框框,能有自己的想法,能大胆的想问题。本环节更能体现老师为学生创设的思考空间,充分调动学生去开动脑筋,大胆把猜想溶于课本内容当中,并且通过这告诉学生,在课堂中要大胆的猜想,大胆去想课本以外的内容。】
2、探讨一个因数扩大,另一个因数缩小,积的变化规律
算一算,想一想,根据18×24=432,你能发现什么规律。
(18÷2)×(24×2)= (18×2)×(24÷2)=
(18÷6)×(24×6)= (18×6)×(24Ο□)=432
(18÷9)×(24×□)=432 (18Ο□)×(24÷3)=432
(引申规律:一个因数乘一个数,另一个因数除以同一个数,积不变。)
【设计意图:这是为有学习余力的孩子特意设计的,也是为”积的变化规律”这节课的完整性设计的。有了此环节,整个内容就变得完整了,但由于此环节所涉及的内容有很大的难度,所以会在此有所保留,提供给有学习余力的孩子来尝试。】
五、质疑问难,思考再现
师:一个因数不变,另一个因数乘(或除以)几(0除外),积也乘(或除以)几。同学们,你们想过没有,一个因数不变,另一个因数加(或减)几,积也会加(或减)几吗?带着这个问题,我们回家想一想,用你认为可行的方法找出答案。
【设计意图:既然在乘法中其中一个因数不变,另一个因数乘或除以几,积就乘或除以几。那么一个因数不变,另一个因数加(或减)也会有这样的变化规律吗?我想,学生一定会很想知道,也会有这样的疑问,因此把这一疑问留给学生回家思考,培养学生的学习热忱,建立拓展延伸、探究问题的意识。】
【板书设计】 积的变化规律
(1)10×2=20(平方厘米)
(2)10×4=40(平方厘米)
(3)10×6=60(平方厘米)
(4)10×8=80(平方厘米)
乘法算式中,一个因数不变,另一个因数乘几(或除以几,0除外)积也乘几(或除以几)。
【设计意图:板书的呈现是随着课程的开展而板演的,课件的演示赋予板书更丰富的内涵,而板书又能辅助课的深入探讨。这样的板书设计能很好的体现本节课的重点内容,且板书书写的顺序指导着学生观察的顺序,从而帮助学生总结出“积的变化规律”。】
10厘米
2厘米
10厘米
4厘米
10厘米
6厘米
10厘米
8厘米
20厘米
2厘米
10厘米
2厘米
(10×2)厘米
(2×2)厘米
PAGE
【教学内容】
人教版义务教育课程标准实验教科书小学数学四年级上册第三单元58页例4。
【教材分析】
《积的变化规律》它是在学生掌握了三位数乘两位数的计算方法的基础上进行教学的。本节课主要引导学生探索当一个因数不变时,另一个因数与积的变化情况,从中归纳出积的变化规律。通过这个过程的探索,不但让学生理解两数相乘时积的变化随其中一个因数的变化而变化,同时使学生经历“积的变化规律”的发现过程,初步获得探索和发现数学规律的基本方法和经验,培养学生迁移类推的能力。
【学生分析】
学生在前段时间刚完成了数与代数领域中的三位数乘两位数的学习。乘法算式中的规律学习是学生第一次接触,这对于学习纯计算问题有着较大的不同,但又有内在的联系。所以运用新的教学手法来调动学生学习本节课的内容是非常必要的。
【设计理念】
本节课,尝试把数与形结合起来学习“积的变化规律”。使只能靠学生想象、推理的纯代数问题转变为可看、可想的空间与图形的问题。把静态的数与数之间的关系转变成为了动态的变化过程,使学生经历通过长与宽的变化促使图形面积变化的过程。形象、生动,更能唤起学生对知识的渴求。整一节课都围绕这一个中心,就是让学生通过图形面积大小的变化来掌握“积的变化规律”,而又把所掌握的规律应用在解决实际问题上。
【教学目标】
1、把数与形结合起来,让学生经历“积的变化规律”整个过程。
2、培养学生用自己的语言来概括“积的变化规律”。
3、运用知识解决实际问题。
4、培养学生主动探究、合作交流和归纳总结的能力,初步养成严谨的治学态度。
【教学重点】
通过数形结合,引导学生自已发现规律、概括规律,进而运用规律。
【教学难点】
把规律运用在实际问题上。
【教学过程】
一、情景导入,初建数模
1、创设情景,引起悬念
课件出示一个长方形,求面积。(课件演示,第一步:出现一个长方形;第二步:里面出现小正方形;第三步:出现长与宽。)
图1:
师:同学们看,这里每个正方形的面积是1平方厘米。长方形的长10厘米表示什么?宽2厘米表示什么?
引导学生说出:长方形的长是10厘米,表示每一行有10小正方形。宽是2厘米,表示这样的小正方形有2行。
师:这个长方形的面积如何算出?表示什么?
引导学生说出:每行有10个小正方形,有2行,10×2=20,一共有20个小正方形,每个小正方形的面积是1平方厘米,就是20平方厘米。
师:老师想把这个长方形的面积变大,你有什么办法?(预设答案:①把长扩大;②把宽扩大;③把长和宽同时扩大。)
师:同学们想的办法都很好,老师决定先采取把宽扩大的方法使这个长方形的面积变大。
2、直观图形面积的变化
长方形的宽扩大2、3、4倍,面积随着变化。
图2:(课件演示宽扩大到原来2倍的过程)
师:怎样列算式求出这个长方形的面积?(10×4=40(平方厘米))
师:长、宽和面积各表示什么?
引导学生说出:长10厘米表示每一行有10个小正方形,宽4厘米表示有4行,一共有40个小正方形。)
图3:(课件演示宽扩大到原来3倍的过程)
师:怎样列算式求出这个长方形的面积?(10×6=60(平方厘米))
师:长、宽和面积各表示什么?
引导学生说出:长10厘米表示每一行有10个小正方形,宽6厘米表示有6行,一共有60个小正方形。)
图4 :(课件演示宽扩大到原来4倍的过程)
师:怎样列算式求出这个长方形的面积?(10×8=80(平方厘米))
师:长、宽和面积各表示什么?
引导学生说出:长10厘米表示每一行有10个小正方形,宽8厘米表示有8行,一共有80个小正方形。)
【设计意图:本环节尝试把数与形结合起来,通过图形面积的变化,使学生能用肉眼看到其中的一个因数变化,使积有所变化的动态演变过程全程显现在学生的面前。借助于“形”的变化,为往后的寻找规律环节做好充分的准备,扫清了学习障碍。】
二、研究问题,寻找规律
1、探索面积随宽的变化而变化的规律
(1)小组讨论
师:先从图1 图4这样顺序观察这四个长方形,什么变了?什么没变?怎么变?再从图4 图1观察,什么变了?什么没变?你能从中找到规律吗?
(学生讨论)
引导学生从上往下对黑板上的式子进行观察、讨论,发现规律。
(1)10×2=20(平方厘米)
(2)10×4=40(平方厘米)
(3)10×6=60(平方厘米)
(4)10×8=80(平方厘米)
(2)汇报交流
(画箭头↓)(穿插课件,出示图形提醒)
引导学生说出:长方形的长不变,宽变了,宽乘2、乘3、乘4……,面积也随着乘2、乘3、乘4……;长不变,宽除以2、除以3、除以4……,面积也会随着除以2、除以3、除以4……。
【设计意图:通过把图形的不断变化随之带来的视觉效果让学生真正感受到“积的变化规律”,有了图形的帮助,使得寻找规律的思路敞开了。学生也能跟着老师一步一个脚印的、扎实的发现并掌握规律。比起单纯的数字游戏活动,印象更深刻更有效果。】
2、探索宽不变,长变化引起面积变化的规律
师:长方形的长不变,宽变化引起了面积的变化。同学们猜想一下,假如长方形的宽不变,长乘2、乘3、乘4……或除以2、除以3、除以4……,也会引起面积有同样的变化吗?
小组讨论,你能以图1来举例说明吗?
预设学生会举例子如:
根据学生的回答,老师列算式。
师:你能根据算式来说说变化的规律吗?
引导学生说出:宽不变,长乘2、乘3、乘4…或长除以2、除以3、除以4……,面积也会跟着乘2、乘3、乘4(或除以2、除以3、除以4……)
【设计意图:通过让学生大胆的猜想,大胆举例来验证长方形的宽不变,长变化了同样也能引起面积的变化规律。使学生在此环节中充分运用自己的经验来解决问题,做到举一反三,并且使学生有自己获取知识的成功感。通过长的变化而引起长方形面积的变化,又是一次视觉的冲击。学生借助图形的变化,会很快找出相应的变化规律。而且在老师的指导下能用比较准确的语言来描述与概括。】
3、整体概括规律
师:在乘法的算式中,乘号前后两个数称为因数。你能把以上所有的算式变化规律用一句话来概括吗?
引导学生用简明的语言表示出来:两数相乘,一个因数不变,另一个因数乘(或除以)几(0除外),积也要乘(或除以)几。(板书规律)并揭示课题:积的变化规律。
三、运用规律,解决问题
师:同学们,从你们刚才的表现老师知道,你们已经学会了“积的变化规律”,但我们不光要掌握它,更重要的是学以致用。
1、基础练习
(1)根据8×50=400,直接写出下面各题的积。(课本P58做一做)
16×50= 32×50= 8×25=
(2)根据7×30=210,直接写出下面各题的得数。
14×30= 21×30= 28×30=
7×60= 7×10= 90×7=
【设计意图:此两个练习主要是围绕着其中一个因数不变,另一个因数乘或除以一个数而展开的。主要的目的是巩固刚刚所寻找到的“积的变化规律”,为下面两个因数的变化而引起积的变化奠定基础,也能从侧面来检查学生对最基本的知识掌握的情况。以此为根据来决定下一个环节的开展程度。】
2、综合练习
师:我们刚刚学会了跟路程有关系的公式:速度×时间=路程。其实,在这公式当中,蕴含着我们本节课的知识在里面,不信你们瞧一瞧!
(根据学生的回答,出现表内黑色字体的数据。)
表一:速度、时间、路程
速度
时间 2小时 4小时 6小时
路程 160千米 320千米 480千米
速度
时间 3小时 3小时 3小时
路程 240千米 480千米 2400千米
师:你能根据以上两个表总结出速度、时间与路程之间的变化规律吗?
引导学生说出在速度不变的情况下,时间乘2、乘3、乘4(或除以2、除以3、除以4……),路程也会乘2、乘3、乘4(或除以2、除以3、除以4……)。反之在时间不变的情况下,速度乘2、乘10(或除以2、除以10)路程也会跟着乘2、乘10(或除以2、除以10)。
表二:单价、数量和总价
师:你能根据(表一)来自己设计“积的变化规律”的数据吗?
单价(元) 数量(本……) 总价(元)
【设计意图:把刚学到的“积的变化规律”马上运用在实际当中。不仅让学生明白到速度、时间与路程三者之间有着怎样紧密的联系,而且也感受到数学知识之间并不是孤立的,知识与知识之间是互相影响着的。学习了的公理或公式都是为了以后的知识学习打基础的。把速度、时间、路程与之联系,极大程度上提高了学生运用知识的能力,也把知识串联起来了。】
3、拓展练习(课本P59第2题)
下面这块长方形绿地的宽要增加到24米,长不变。扩大后的绿地面积是多少?
引导学生利用那个本节课所学到的“积的变化规律”来解决本题。
【设计意图:在新授的同时穿插相关的练习,使学生掌握得更牢固,也加深了印象。我们知道孩子的瞬间记忆是非常强的,假如我们能加以运用,肯定会达到事半功倍的效果。所以整一个环节,都采取了边讲边练的形式。】
四、拓展升华,继续探索
(这部分内容作为弹性要求,视学生学习情况决定是否出现)
1、探索两个因数同时扩大(或缩小),积的变化规律
课件演示长方形从原来的10厘米,宽2厘米。长乘2、宽也乘2,面积的变化。
原来的长方形:
面积是:10×2=20 (平方厘米)
变为:
面积是:(10×2)×(2×2)=80(平方厘米)
师:把长方形的长和宽同时乘2 ,这个长方形的面积会如何变化?为什么?(面积会扩大4倍。因为长乘以2,宽也乘以2,一共乘了4,所以面积也要乘以4.)
(引申规律:一个因数乘以一个数,另一个因数乘以另一个数,积就乘这两个数的积。)
【设计意图:这是“积的变化规律”的又一次升华。引导学生探究当两个因数都发生变化时,积是如何变化的。目的是让学生能跳出书本的框框,能有自己的想法,能大胆的想问题。本环节更能体现老师为学生创设的思考空间,充分调动学生去开动脑筋,大胆把猜想溶于课本内容当中,并且通过这告诉学生,在课堂中要大胆的猜想,大胆去想课本以外的内容。】
2、探讨一个因数扩大,另一个因数缩小,积的变化规律
算一算,想一想,根据18×24=432,你能发现什么规律。
(18÷2)×(24×2)= (18×2)×(24÷2)=
(18÷6)×(24×6)= (18×6)×(24Ο□)=432
(18÷9)×(24×□)=432 (18Ο□)×(24÷3)=432
(引申规律:一个因数乘一个数,另一个因数除以同一个数,积不变。)
【设计意图:这是为有学习余力的孩子特意设计的,也是为”积的变化规律”这节课的完整性设计的。有了此环节,整个内容就变得完整了,但由于此环节所涉及的内容有很大的难度,所以会在此有所保留,提供给有学习余力的孩子来尝试。】
五、质疑问难,思考再现
师:一个因数不变,另一个因数乘(或除以)几(0除外),积也乘(或除以)几。同学们,你们想过没有,一个因数不变,另一个因数加(或减)几,积也会加(或减)几吗?带着这个问题,我们回家想一想,用你认为可行的方法找出答案。
【设计意图:既然在乘法中其中一个因数不变,另一个因数乘或除以几,积就乘或除以几。那么一个因数不变,另一个因数加(或减)也会有这样的变化规律吗?我想,学生一定会很想知道,也会有这样的疑问,因此把这一疑问留给学生回家思考,培养学生的学习热忱,建立拓展延伸、探究问题的意识。】
【板书设计】 积的变化规律
(1)10×2=20(平方厘米)
(2)10×4=40(平方厘米)
(3)10×6=60(平方厘米)
(4)10×8=80(平方厘米)
乘法算式中,一个因数不变,另一个因数乘几(或除以几,0除外)积也乘几(或除以几)。
【设计意图:板书的呈现是随着课程的开展而板演的,课件的演示赋予板书更丰富的内涵,而板书又能辅助课的深入探讨。这样的板书设计能很好的体现本节课的重点内容,且板书书写的顺序指导着学生观察的顺序,从而帮助学生总结出“积的变化规律”。】
10厘米
2厘米
10厘米
4厘米
10厘米
6厘米
10厘米
8厘米
20厘米
2厘米
10厘米
2厘米
(10×2)厘米
(2×2)厘米
PAGE
