上海市浦东新区2018-2019学年高二上学期期中质量检测数学试题
文档属性
| 名称 | 上海市浦东新区2018-2019学年高二上学期期中质量检测数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 345.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-13 08:01:58 | ||
图片预览


文档简介
2018-2019学年第一学期高二年级数学质量检测
高二年级数学
总分:100分 时间:90分钟 2018年11月
一、填空题(每小题3分,共12题,满分36分)
3
2. 行列式中的代数余子式是
3.已知向量=(2,3),=(﹣2,1),则在方向上的投影等于 ﹣ .
-40
5.数列{}中,,,且满足
数列{}的递推公式是
6.关于、的二元线性方程组的增广矩阵经过变换,最后得到的矩阵为,则二阶行列式= .
7.设,是平面直角坐标系的x轴、y轴正方向上的单位向量,且=4+2,=3+4,则△ABC的面积等于 5
8.用数学归纳法证明“1+++…+<n(n∈N*,n>1)”时,由n=k(k>1)不等式成立,推证n=k+1时,左边应增加的项数共______项.;
9.已知数列是无穷等比数列,其前n项和是,若,,
则的值为 . 4
10、已知直角三角形ABC中,,那么m=___
m=-2
_____
12.设点,,在轴上求一点,使最小,此时
二、选择题(每小题3分,共4题,满分12分)
13.下列命题正确的是( C )
A.单位向量都相等
B.若与共线,与共线,则与共线
C.若|+|=|﹣|,则?=0
D.若与都是单位向量,则?=1
14.在等比数列{an}中,若a4,a8是方程x2+4x+3=0的两个根,则a6的值是( B )
A.± B.-
C. D.±3
15.已知=(5,4),=(3,2),则与2﹣3平行的单位向量为( B )
A.(,) B.(,)或(﹣,﹣)
C.(,﹣)或(﹣,) D.(﹣,﹣)
16.已知等比数列{an}的公比为q,其前n项的和Sn,若集合M={S|S=,q≠-1},则M等于 ( D )
A. {0} B. {0,} C. {,1} D. {0,,1}
三、解答题(共5小题,满分52分,解答要有详细的论证过程与运算步骤)
17.(本题满分8分)数列的通项公式是,前项和为,
计算(1)
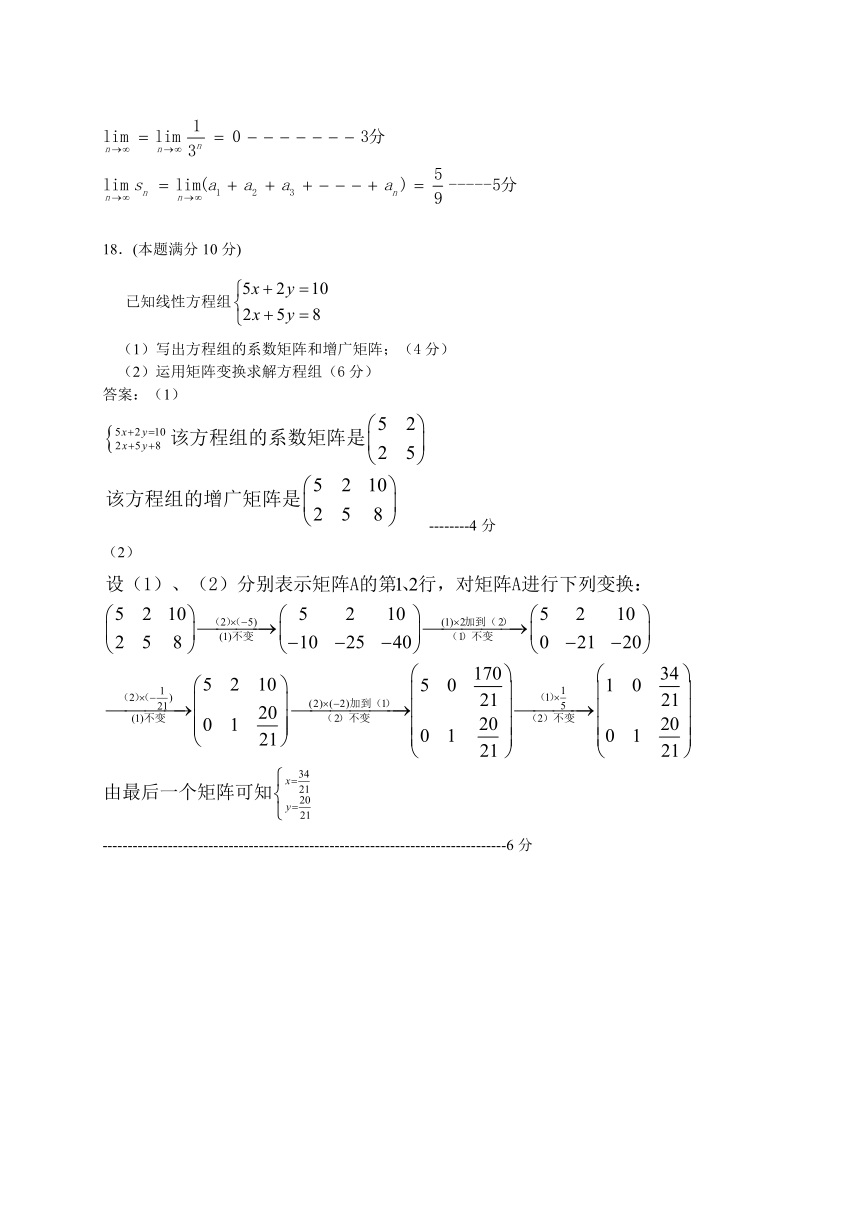
18.(本题满分10分)
已知线性方程组
(1)写出方程组的系数矩阵和增广矩阵;(4分)
(2)运用矩阵变换求解方程组(6分)
答案:(1)
--------4分
(2)
--------------------------------------------------------------------------------6分
..............................................10分
20.(本题满分10分)已知是平面内两个不共线的非零向量,,,,且三点共线.
(1)求实数的值;(5分)
(2)已知,点,若四点按逆时针顺序构成平行四边形,求点的坐标.(5分)
解:
(1)=+=(2e1+e2)+(-e1+λe2)=e1+(1+λ)e2.∵A,E,C三点共线,
∴存在实数k,使得=k,
即e1+(1+λ)e2=k(-2e1+e2),
得(1+2k)e1=(k-1-λ)e2.
∵e1,e2是平面内两个不共线的非零向量,
∴,解得k=-,λ=-.-----------------------------5
---------------------------------5分
2.(本题满分14分)已知数列的前项和为,且 .
(Ⅰ)求数列的通项公式;
(Ⅱ)设,数列的前项和为,求使不等式对一切都成立的最大正整数的值;
(Ⅲ)设是否存在,使得
成立?若存在,求出的值;若不存在,请说明理由.
解:
(Ⅰ)当时, ……………… 1分
当时, .…… 2分
而当时,
∴. ………………4分
(Ⅱ)
∴……
………………7分
∵
∴单调递增,故. ………………8分
令,得,所以. ……………… 10分
(Ⅲ)
(1)当为奇数时,为偶数, ∴,.
………………1 2分
(2)当为偶数时,为奇数, ∴,(舍去).
综上,存在唯一正整数,使得成立.
……………………1 4分
同课章节目录
