【一课一练】第六单元 第4课时组合图形的面积(含答案)
文档属性
| 名称 | 【一课一练】第六单元 第4课时组合图形的面积(含答案) | 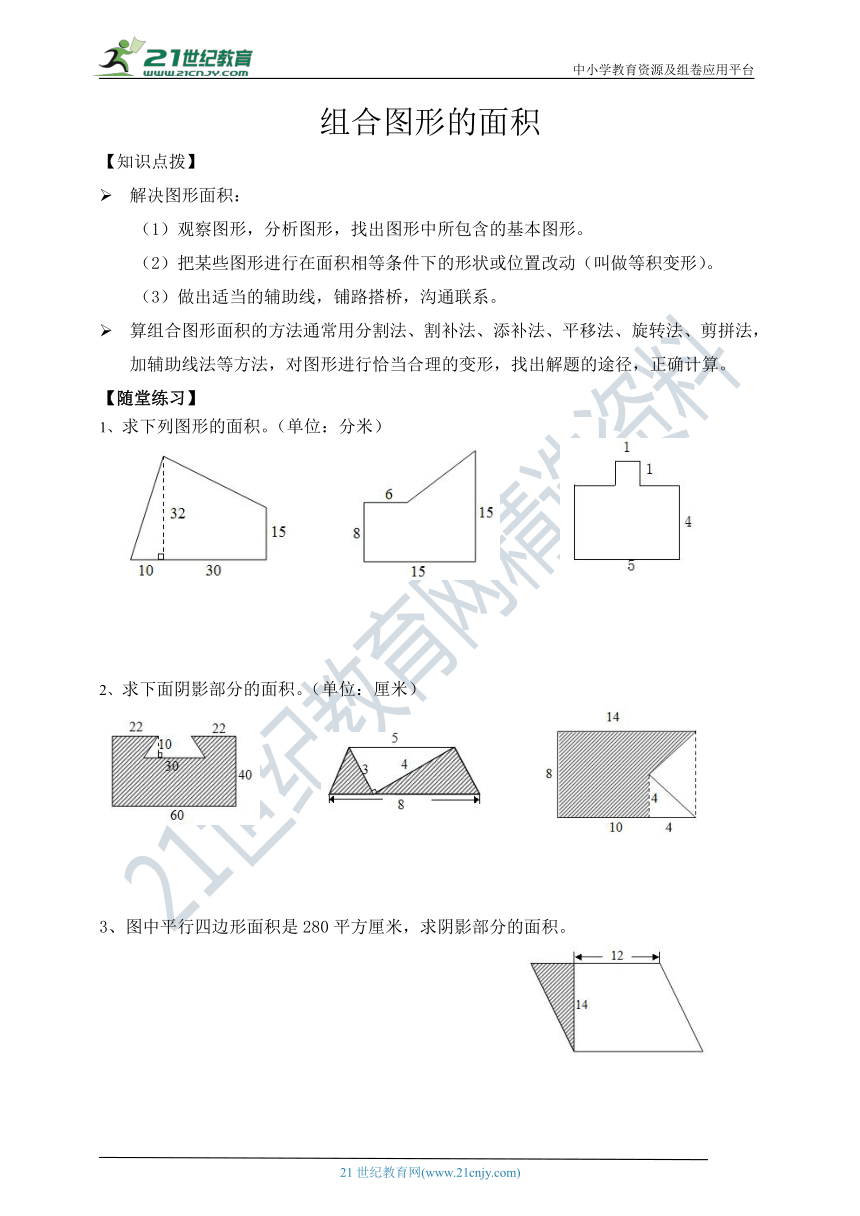 | |
| 格式 | zip | ||
| 文件大小 | 195.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-14 09:38:16 | ||
图片预览


文档简介
组合图形的面积
【知识点拨】
解决图形面积:
(1)观察图形,分析图形,找出图形中所包含的基本图形。
(2)把某些图形进行在面积相等条件下的形状或位置改动(叫做等积变形)。
(3)做出适当的辅助线,铺路搭桥,沟通联系。
算组合图形面积的方法通常用分割法、割补法、添补法、平移法、旋转法、剪拼法,加辅助线法等方法,对图形进行恰当合理的变形,找出解题的途径,正确计算。
【随堂练习】
1、求下列图形的面积。(单位:分米)
2、求下面阴影部分的面积。(单位:厘米)
3、图中平行四边形面积是280平方厘米,求阴影部分的面积。
4、用“割补”或“扩展”法求下图中各图形的面积。(每一方格为1cm2)
5、如图,大正方形和小正方形的边长分别是4厘米和3厘米,求阴影部分的面积。
6、如下图是两个正方形组成的,已知大正方形边长10分米,小正方形的边长7分米,求阴影部分的面积。
7、如图,ABCD是长8厘米,宽为6厘米的长方形,AF是4厘米,求△AEF。(阴影部分的面积)
8、如图,求阴影部分的面积之差。(单位:cm)
【随堂练习】参考答案
1、求下列图形的面积。(单位:分米)
2、求下面阴影部分的面积。(单位:厘米)
3、图中平行四边形面积是280平方厘米,求阴影部分的面积。
解:280÷14=20cm
(20-12)×14÷2=56cm2
4、用“割补”或“扩展”法求下图中各图形的面积。(每一方格为1cm2)
S①=8.5cm2
S②=5.5cm2
S③=10cm2
5、如图,大正方形和小正方形的边长分别是4厘米和3厘米,求阴影部分的面积。
解:4×4+3×3=25cm2
4×(4+3)÷2=14cm2
3×3÷2=4.5cm2
25-14-4.5=6.5cm2
答:阴影部分的面积6.5cm2
6、如下图是两个正方形组成的,已知大正方形边长10分米,小正方形的边长7分米,求阴影部分的面积。
解:10×10+7×7=149dm2
7×(10+7)÷2=59.5dm2
10×10÷2=50dm2
149-59.5-50=39.5dm2
答:阴影部分的面积39.5dm2
7、如图,ABCD是长8厘米,宽为6厘米的长方形,AF是4厘米,求△AEF。(阴影部分的面积)
解:△AEB:8×6÷2=24cm2
△AFB:4×6÷2=12cm2
△AEF: 24-12=12cm2
答:阴影部分的面积12cm2
8、如图,求阴影部分的面积之差。(单位:cm)
解:△CEB:(10+12)×12÷2=132cm2
四边形ABCD:12×12=144cm2 144-132=12cm2
答:阴影部分的面积之差12cm2
【知识点拨】
解决图形面积:
(1)观察图形,分析图形,找出图形中所包含的基本图形。
(2)把某些图形进行在面积相等条件下的形状或位置改动(叫做等积变形)。
(3)做出适当的辅助线,铺路搭桥,沟通联系。
算组合图形面积的方法通常用分割法、割补法、添补法、平移法、旋转法、剪拼法,加辅助线法等方法,对图形进行恰当合理的变形,找出解题的途径,正确计算。
【随堂练习】
1、求下列图形的面积。(单位:分米)
2、求下面阴影部分的面积。(单位:厘米)
3、图中平行四边形面积是280平方厘米,求阴影部分的面积。
4、用“割补”或“扩展”法求下图中各图形的面积。(每一方格为1cm2)
5、如图,大正方形和小正方形的边长分别是4厘米和3厘米,求阴影部分的面积。
6、如下图是两个正方形组成的,已知大正方形边长10分米,小正方形的边长7分米,求阴影部分的面积。
7、如图,ABCD是长8厘米,宽为6厘米的长方形,AF是4厘米,求△AEF。(阴影部分的面积)
8、如图,求阴影部分的面积之差。(单位:cm)
【随堂练习】参考答案
1、求下列图形的面积。(单位:分米)
2、求下面阴影部分的面积。(单位:厘米)
3、图中平行四边形面积是280平方厘米,求阴影部分的面积。
解:280÷14=20cm
(20-12)×14÷2=56cm2
4、用“割补”或“扩展”法求下图中各图形的面积。(每一方格为1cm2)
S①=8.5cm2
S②=5.5cm2
S③=10cm2
5、如图,大正方形和小正方形的边长分别是4厘米和3厘米,求阴影部分的面积。
解:4×4+3×3=25cm2
4×(4+3)÷2=14cm2
3×3÷2=4.5cm2
25-14-4.5=6.5cm2
答:阴影部分的面积6.5cm2
6、如下图是两个正方形组成的,已知大正方形边长10分米,小正方形的边长7分米,求阴影部分的面积。
解:10×10+7×7=149dm2
7×(10+7)÷2=59.5dm2
10×10÷2=50dm2
149-59.5-50=39.5dm2
答:阴影部分的面积39.5dm2
7、如图,ABCD是长8厘米,宽为6厘米的长方形,AF是4厘米,求△AEF。(阴影部分的面积)
解:△AEB:8×6÷2=24cm2
△AFB:4×6÷2=12cm2
△AEF: 24-12=12cm2
答:阴影部分的面积12cm2
8、如图,求阴影部分的面积之差。(单位:cm)
解:△CEB:(10+12)×12÷2=132cm2
四边形ABCD:12×12=144cm2 144-132=12cm2
答:阴影部分的面积之差12cm2
