人教版高中物理选修3-3 8.1 气体的等温变化 课件:22张PPT
文档属性
| 名称 | 人教版高中物理选修3-3 8.1 气体的等温变化 课件:22张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2018-11-14 00:00:00 | ||
图片预览




文档简介
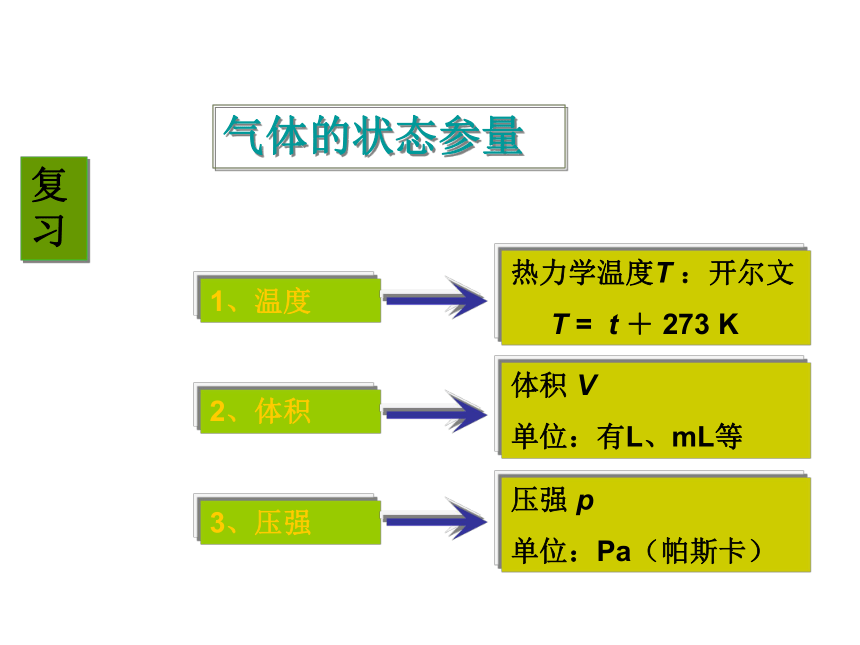
课件22张PPT。1、气体的等温变化1、温度2、体积3、压强热力学温度T :开尔文
T = t + 273 K体积 V
单位:有L、mL等压强 p
单位:Pa(帕斯卡)气体的状态参量复习如何确定气体的状态参量呢?温度( T )----------温度计
体积( V )----------容器的容积
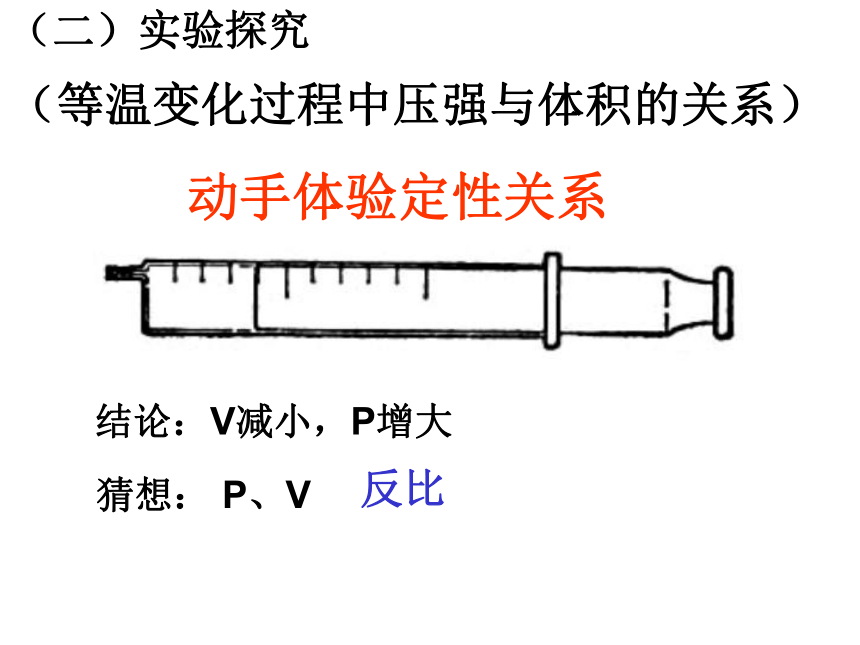
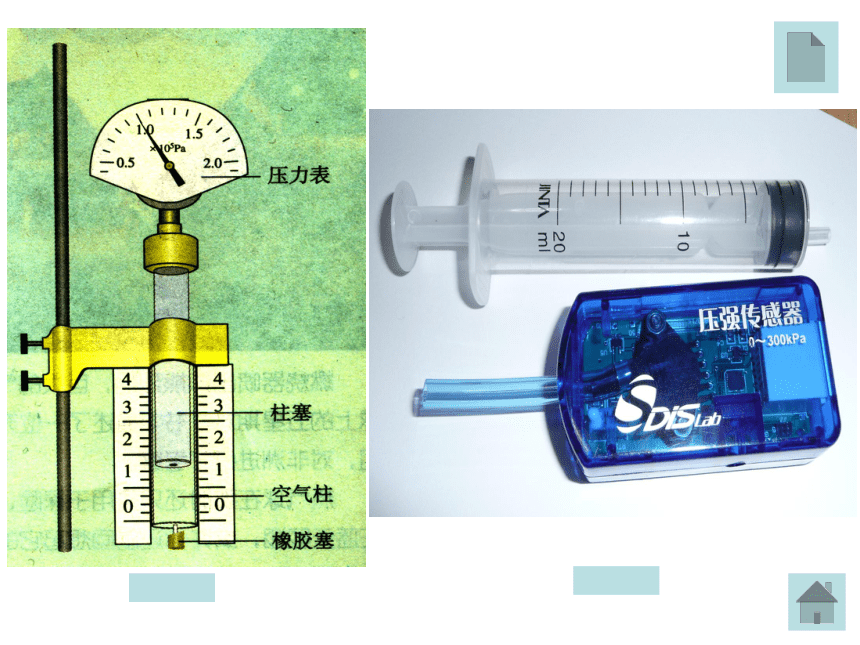
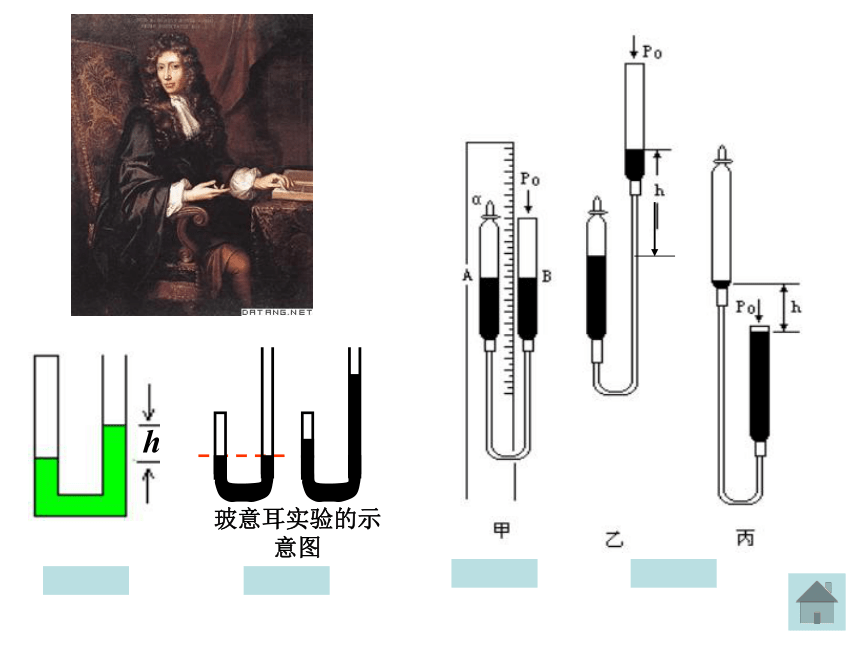
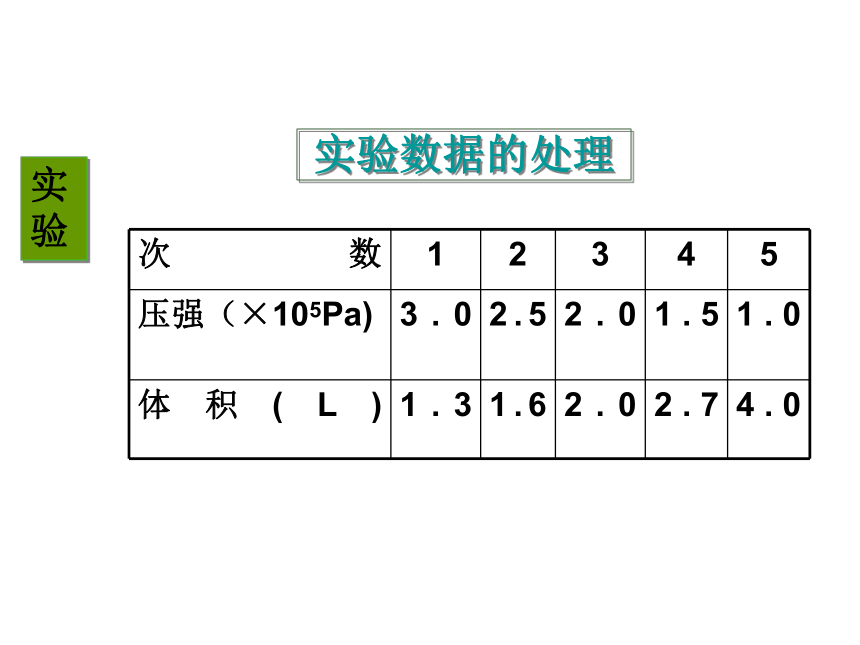
压强( p )-----------气压计动手体验定性关系(等温变化过程中压强与体积的关系)(二)实验探究结论:V减小,P增大猜想: P、V反比定量研究: 设计一个实验研究一定质量的气体在等温变化过程中压强与体积的定量关系(二)实验探究猜想: P、V反比横截面积S实验数据的处理实验V123012341/V12300.20.40.60.8实验探究结论: 在温度不变时,压强p和体积V成反比。 一定质量的气体,在温度不变的情况下,它的压
强跟体积成反比(三)玻意耳定律 1、内容:2、表达式:3、图像:4、适用范围:温度不太低,压强不太大1、一定质量的气体,在做等温变化的过程中,下列物理量发生变化的有:( )
A、气体的体积
B、单位体积内的分子数
C、气体的压强
D、分子总数例1: 一贮气筒内装有25L、1.0×105 Pa 的空气,现想使筒内气体压强增至4.0×105Pa,且保持温度不变,那么应向筒内再打入 L、1.0×105 Pa 的相同温度的气体。V12301234二.等温变化图象
1、特点:
(1)等温线是双曲线的一支。(2)温度越高,其等温线离原点越远. 同一气体,不同温度下等温线是不同的,你能判断那条等温线是表示温度较高的情形吗?你是根据什么理由作出判断的?结论:t3>t2>t1例2. 如图8.1—2所示,A、B 是一定质量的理想气体在两条等温线上的两个状态点,这两点与坐标原点O 和对应坐标轴上的VA、VB坐标所围成的三角形面积分别为SA 、SB,对应温度分别为TA和TB,则 ( )
SA > SB TA > TB
SA = SB TA < TB
SA < SB TA < TB
SA > SB TA < TB2、图象意义(1)物理意义:反映压强随体积的变化关系(2)点意义:每一组数据---反映某一状态 (3)结论:体积缩小到原来的几分之一,压强增大到原来的几倍.体积增大到原来的几倍,它的压强就减小为原来的几分之一.用气体定律解题的步骤1.确定研究对象.被封闭的气体(满足质量不变的条件);2.用一定的数字或表达式写出气体状态的初始条件(p1,V1,T1,p2,V2,T2);3.根据气体状态变化过程的特点,列出相应的气体公式(本节课中就是玻意耳定律公式);4.将各初始条件代入气体公式中,求解未知量;5.对结果的物理意义进行讨论.例题:一定质量气体的体积是20L时,压强为1×105Pa。当气体的体积减小到16L时,压强为多大?设气体的温度保持不变。 答案: 1.25×10 5Pa例4. ?某个容器的容积是10L,所装气体的压强是20×105Pa。如果温度保持不变,把容器的开关打开以后,容器里剩下的气体是原来的百分之几?设大气压是1.0×105Pa。解 ?设容器原装气体为研究对象。初态? p1=20×105Pa V1=10L T1=T
末态? p2=1.0×105Pa V2=?L T2=T由玻意耳定律? p1V1=p2V2得即剩下的气体为原来的5%。就容器而言,里面气体质量变了,似乎是变质量问题了,但若视容器中气体出而不走,就又是质量不变了。
T = t + 273 K体积 V
单位:有L、mL等压强 p
单位:Pa(帕斯卡)气体的状态参量复习如何确定气体的状态参量呢?温度( T )----------温度计
体积( V )----------容器的容积
压强( p )-----------气压计动手体验定性关系(等温变化过程中压强与体积的关系)(二)实验探究结论:V减小,P增大猜想: P、V反比定量研究: 设计一个实验研究一定质量的气体在等温变化过程中压强与体积的定量关系(二)实验探究猜想: P、V反比横截面积S实验数据的处理实验V123012341/V12300.20.40.60.8实验探究结论: 在温度不变时,压强p和体积V成反比。 一定质量的气体,在温度不变的情况下,它的压
强跟体积成反比(三)玻意耳定律 1、内容:2、表达式:3、图像:4、适用范围:温度不太低,压强不太大1、一定质量的气体,在做等温变化的过程中,下列物理量发生变化的有:( )
A、气体的体积
B、单位体积内的分子数
C、气体的压强
D、分子总数例1: 一贮气筒内装有25L、1.0×105 Pa 的空气,现想使筒内气体压强增至4.0×105Pa,且保持温度不变,那么应向筒内再打入 L、1.0×105 Pa 的相同温度的气体。V12301234二.等温变化图象
1、特点:
(1)等温线是双曲线的一支。(2)温度越高,其等温线离原点越远. 同一气体,不同温度下等温线是不同的,你能判断那条等温线是表示温度较高的情形吗?你是根据什么理由作出判断的?结论:t3>t2>t1例2. 如图8.1—2所示,A、B 是一定质量的理想气体在两条等温线上的两个状态点,这两点与坐标原点O 和对应坐标轴上的VA、VB坐标所围成的三角形面积分别为SA 、SB,对应温度分别为TA和TB,则 ( )
SA > SB TA > TB
SA = SB TA < TB
SA < SB TA < TB
SA > SB TA < TB2、图象意义(1)物理意义:反映压强随体积的变化关系(2)点意义:每一组数据---反映某一状态 (3)结论:体积缩小到原来的几分之一,压强增大到原来的几倍.体积增大到原来的几倍,它的压强就减小为原来的几分之一.用气体定律解题的步骤1.确定研究对象.被封闭的气体(满足质量不变的条件);2.用一定的数字或表达式写出气体状态的初始条件(p1,V1,T1,p2,V2,T2);3.根据气体状态变化过程的特点,列出相应的气体公式(本节课中就是玻意耳定律公式);4.将各初始条件代入气体公式中,求解未知量;5.对结果的物理意义进行讨论.例题:一定质量气体的体积是20L时,压强为1×105Pa。当气体的体积减小到16L时,压强为多大?设气体的温度保持不变。 答案: 1.25×10 5Pa例4. ?某个容器的容积是10L,所装气体的压强是20×105Pa。如果温度保持不变,把容器的开关打开以后,容器里剩下的气体是原来的百分之几?设大气压是1.0×105Pa。解 ?设容器原装气体为研究对象。初态? p1=20×105Pa V1=10L T1=T
末态? p2=1.0×105Pa V2=?L T2=T由玻意耳定律? p1V1=p2V2得即剩下的气体为原来的5%。就容器而言,里面气体质量变了,似乎是变质量问题了,但若视容器中气体出而不走,就又是质量不变了。
