江苏省徐州市2019届高三上学期期中质量抽测数学试题(WORD版)
文档属性
| 名称 | 江苏省徐州市2019届高三上学期期中质量抽测数学试题(WORD版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-16 14:48:15 | ||
图片预览




文档简介
绝密★启用前
2019届徐州市高三第一学期期中抽测考试
数学I
一.填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应位置.
1.已知集合,,则 ▲ .
2.若复数满足(其中为虚数单位),则的模为 ▲ .
3.某水产养殖场利用100个网箱养殖水产品,收获时测量各箱水产品的产量(单位:kg),其频率分布直方图如图所示,则该养殖场有 ▲ 个网箱产量不低于50 kg.
4. 右图是一个算法的流程图,则输出的的值是 ▲ .
5.已知双曲线的离心率为,则实数的值为 ▲ .
6.已知袋中装有大小相同、质地均匀的2个红球和3个白球,从中一次摸出2个,恰有1个是红球的概率为 ▲ .
7. 已知等差数列的前项和为,,,则的值为 ▲ .
8. 已知函数,若,且,则的最大值为 ▲ .
9. 已知奇函数是R上的单调函数,若函数只有一个零点,则实数的值为 ▲ .
10.如图,已知正方体的棱长为1,点为棱上任意一点,则四棱锥的体积为 ▲ .
11.在平行四边形中,,,,若 ,则的值
为 ▲ .
12.已知正实数 满足,则 的最小值为 ▲ .
13. 过点的直线与圆交于两点,若是的中点,则实数的取值范围是 ▲ .
14.已知函数,若有三个零点,则实数的取值范围是 ▲ .
二.解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或计算步骤.
15.(本小题满分14分)
在△中,角的对边分别为,已知.
(1)求角的值;
(2)若,,求的面积.
16.(本小题满分14分)
如图,在三棱锥中, 分别为,的中点,点在上,且底面.
(1)求证:平面;
(2)若,求证:平面平面.
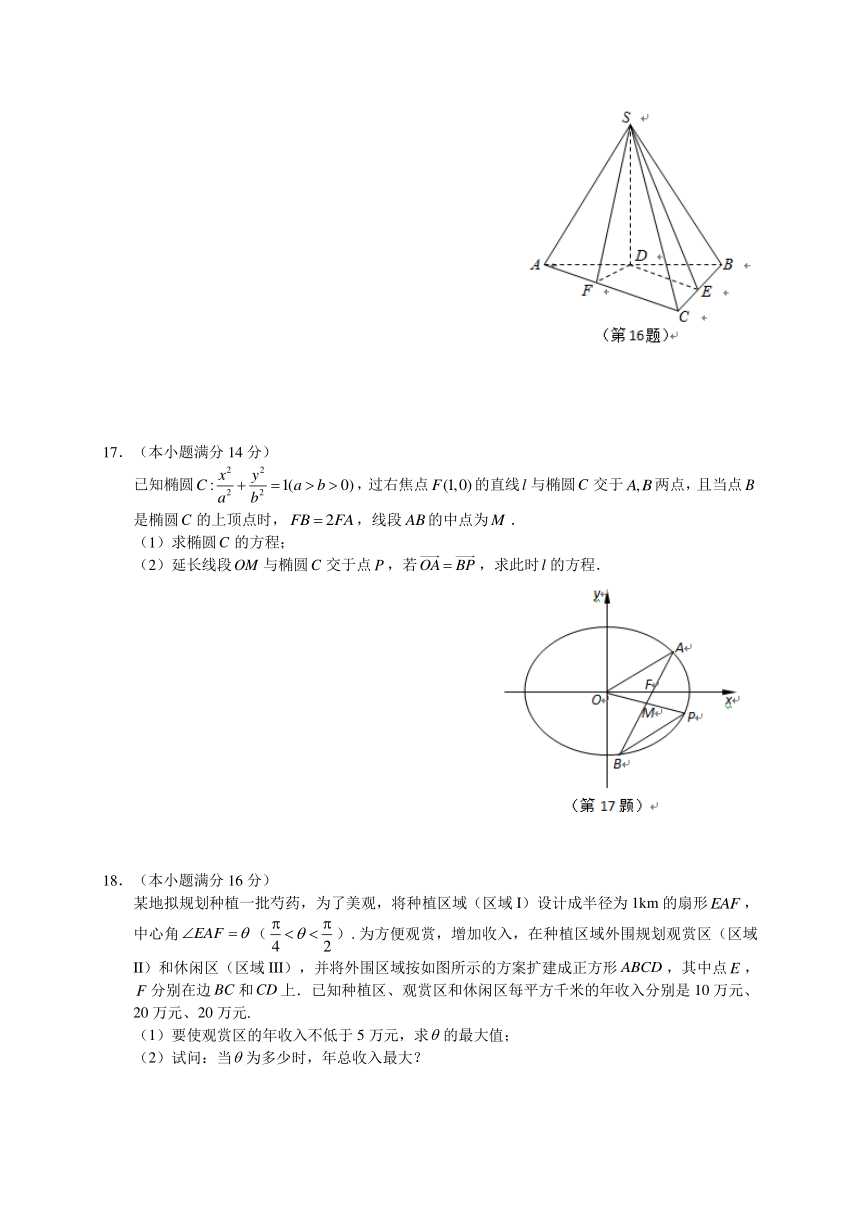
17.(本小题满分14分)
已知椭圆,过右焦点的直线与椭圆交于两点,且当点是椭圆的上顶点时,,线段的中点为.
(1)求椭圆的方程;
(2)延长线段与椭圆交于点,若,求此时的方程.
18.(本小题满分16分)
某地拟规划种植一批芍药,为了美观,将种植区域(区域I)设计成半径为1km的扇形,中心角().为方便观赏,增加收入,在种植区域外围规划观赏区(区域II)和休闲区(区域III),并将外围区域按如图所示的方案扩建成正方形,其中点,分别在边和上.已知种植区、观赏区和休闲区每平方千米的年收入分别是10万元、20万元、20万元.
(1)要使观赏区的年收入不低于5万元,求的最大值;
(2)试问:当为多少时,年总收入最大?
19.(本小题满分16分)
设函数,.
(1)当时,求函数的在点处的切线方程;
(2)讨论函数的单调性,并写出单调区间;
(3)当时,若函数有唯一零点,求实数的值.
20.(本小题满分16分)
已知数列各项均为正数,,,且对任意恒成立.
(1)若,求的值;
(2)若,(i)求证:数列是等差数列;(ii)在数列中,对任意,总存在,(其中),使构成等比数列,求出符合条件的一组.
数学II(附加题)
21.【选做题】在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.请在答卷纸指定区域内作答.解答应写出文字说明、证明过程或演算步骤.
A.选修4—1:几何证明选讲(本小题满分10分)
如图,⊙O的半径OB垂直于直径AC,D为AO上一点,BD的延长线交⊙O于点E,过E点的圆的切线交CA的延长线于点P。
求证:PD2=PA?PC
B.选修4—2:矩阵与变换(本小题满分10分)
已知矩阵M=,且属于特征值2的一个特征向量为,在平面直角坐标系xoy中,眯A(0,0),B(1,0),C(2,3)在矩阵M对应的变换作用下得到的点分别为,求△的面积。
C.选修4—4:坐标系与参数方程(本小题满分10分)
在极坐标系中,直线l的极坐标方程为+1=0。以极点O为坐标原点,极轴正方向为x轴正方向建立平面直角坐标系xoy,曲线C的参数方程为(θ为参数,r>0),若直线l与曲线C交于A,B两点,且AB=,求r的值。
D.选修4—5:不等式选讲(本小题满分10分)
对于实数x,y,若满足|x-1|≤1,|y-2|≤1,求|x-2y+1|的最大值.
【必做题】第22题、第23题,每题10分,共计20分.请在答卷卡指定区域内作答.解答应写出
文字说明、证明过程或演算步骤.
22.(本小题满分10分)
在某次投篮测试中,有两种投篮方案:方案甲:先在A点投篮一次,以后都在B点投篮;方案乙:始终在B点投篮。每次投篮之间相互独立。某选手在A点命中的概率为,命中一次记3分,没有命中得0分;在B点命中的概率为,命中一次记2分,没有命中得0分,用随机变量表示该选手一次投篮测试的累计得分,如果的值不低于3分,则认为其通过测试并停止投篮,否则继续投篮,但一次测试最多投篮3次。
(1)若该选手选择方案甲,求测试结束后所得分的分布列和数列期望。
(2)试问该选手选择哪种方案通过测试的可能性较大?请说明理由。
23.(本小题满分10分)
(1)证明:为偶数(n∈N*);
(2)证明:大于的最小整数能被整除(n∈N*)。
参考答案
1、{2,4} 2、 3、82 4、8 5、2
6、 7、24 8、 9、 10、
11、 12、18 13、或 14、
15、
16、
(1)由中位线知:DE‖AC,可证:DE‖平面SAC
(2)由SD⊥平面ABC,知SD⊥AC,又SF⊥AC,SD与SF交于点S,
所以,AC⊥平面SFD,所以,平面SAC⊥平面SFD
17、
18、
19、
20、
2018-2019学年度高三年级第一学期期中抽测
数学Ⅱ参考答案及评分标准
A.连结OE,因为PE切⊙O于点E,所以∠OEP=900,所以∠OEB+∠BEP=900,
因为OB=OE,所以∠OBE=∠OEB,因为OB⊥AC于点O,
所以∠OBE+∠BDO=900.…………………………………5分
故∠BEP=∠BDO=∠PDE,所以PD=PE,又因为PE切⊙O于点E,所以PE2=PA·PC,
故PD2=PA·PC.………………………………………………………………………10分
B.因,所以,所以,……………………………………2分
,,,即.…………6分
故. ……………………………………………………10分
C.由,得,
即直线l的方程为. ………………………………………………3分
由,得曲线的普通方程为,
故曲线C是圆心坐标为,半径为的圆 ,……………………………………6分
所以,圆心到直线的距离,由,则.……………… 10分
D.由…………………………………………………4分
,…………………8分
当且仅当时,取“”.
可知,的最大值为5.…………………………………………………10分
22.(1)在A点投篮命中记作,不中记作;在B点投篮命中记作,不中记作,
其中, …………………2分
的所有可能取值为,则
,…………………………3分
,……………………………4分
,…………………………………………………………5分
.…………………………6分
的分布列为: ,,,.
所以,
所以,的数学期望为.…………………………………………………………7分
(2)选手选择方案甲通过测试的概率为,
选手选择方案乙通过测试的概率为
,………………………9分
因为,所以该选手应选择方案甲通过测试的概率更大.……………………10分
23.(1)因为,
所以为偶数(n∈N*). ………………………………………4分
(2)注意到,则大于的最小正整数必为
,记为2kN,
又因为
而由(1)同理可得必为偶数,记为,
所以,,
即能被整除,从而命题得证. ……………………………………………10分
注 意 事 项
考生在答题前请认真阅读本注意事项及各题答题要求
1.本试卷共4页,均为非选择题(第1题~第20题,共20题)。本卷满分为160分,考试
时间为120分钟。考试结束后,请将本试卷和答题卡一并交回。
2.答题前,请您务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及
答题卡的规定位置。
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与您本人是否相符。
4.作答试题,必须用0.5毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置
作答一律无效。
5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗。
同课章节目录
