九年级数学24.3《正多边形和圆》同步提高测试(含答案)
文档属性
| 名称 | 九年级数学24.3《正多边形和圆》同步提高测试(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 264.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-17 10:19:42 | ||
图片预览


文档简介
九年级数学24.3《正多边形和圆》同步提高测试
一、选择题:
1、如图所示,正六边形ABCDEF内接于⊙O,则∠ADB的度数是( ).
A.60° B.45° C.30° D.22.5°
2、正多边形的一边所对的中心角与它的一个外角的关系是( )
A.相等????????B.互余?????C.互补????D.互余或互补
3、正六边形的半径是6,则这个正六边形的面积为( )
A.24 B.54
C. D.
4、如图,正六边形ABCDEF内接于⊙O,若⊙O的半径为6,则阴影部分的面积为( )
A.12π??????B.6π? C.9π? D.18π
5、已知圆内接正三角形的面积为,则该圆的内接正六边形的边心距是( )
A.2 B.1 C. D.
6、如图,⊙O内切于正方形ABCD,边BC、DC上两点M、N,且MN是⊙O的切线,当△AMN的面积为4时,则⊙O的半径r是( )
A. B. C.2 D.
在△ABC中,∠ACB=90°,∠B=15°,以C为圆心,CA长为半径的圆交AB于D,如图所示,若AC=6,则AD的长为( ).
A.π??????B.6π? C.3π? D.1.5π
8、如图,要拧开一个边长为a=6 mm的正六边形螺帽,扳手张开的开口b至少为( )
A.6 mm B.12 mmC.6 mm D.4 mm
9、如图所示,△ABC为⊙O的内接三角形,AB=1,∠C=30°,则⊙O的内接正六边形的面积为( )
A.2??????B.6? C.9? D.3
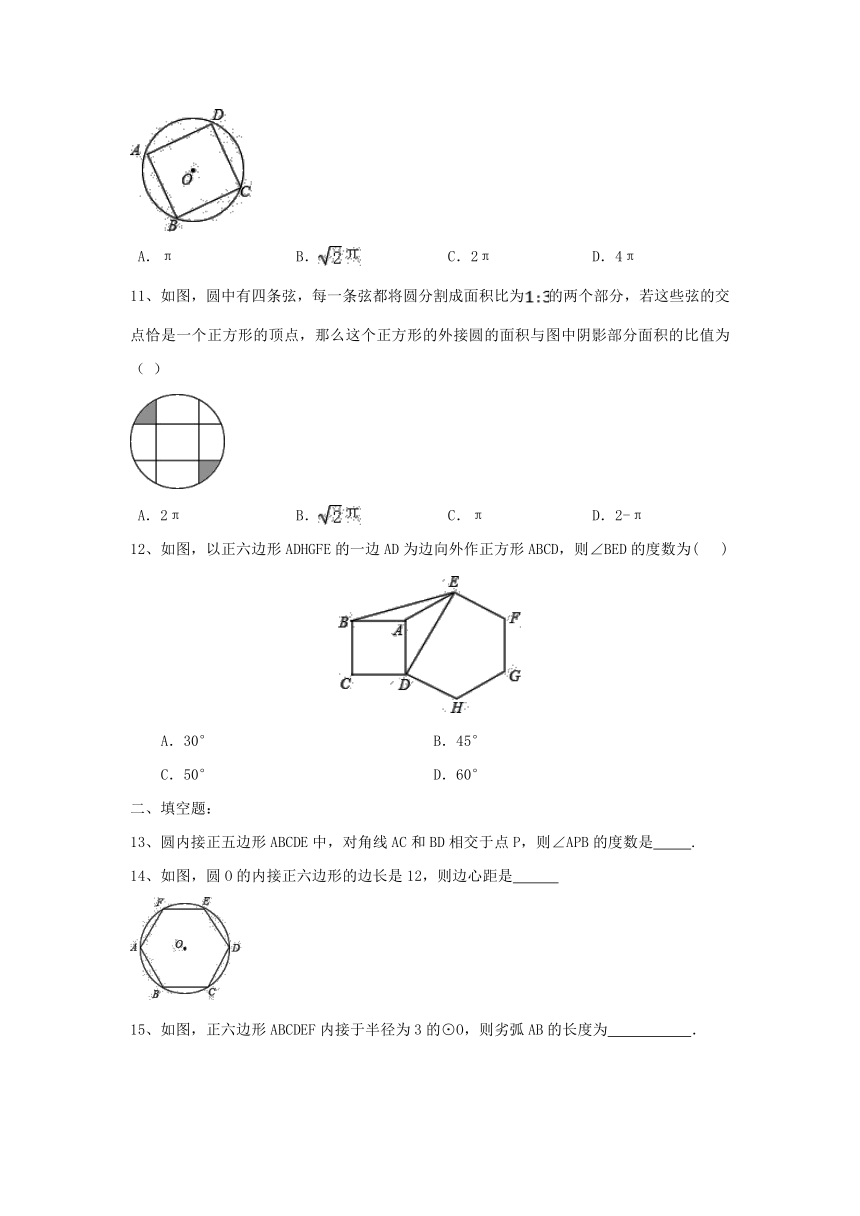
10、如图,用一张圆形纸片完全覆盖边长为2的正方形ABCD,则该圆形纸片的面积最少为( )
A.π B. C.2π D.4π
11、如图,圆中有四条弦,每一条弦都将圆分割成面积比为的两个部分,若这些弦的交点恰是一个正方形的顶点,那么这个正方形的外接圆的面积与图中阴影部分面积的比值为( )
A.2π B. C.π D.2-π
12、如图,以正六边形ADHGFE的一边AD为边向外作正方形ABCD,则∠BED的度数为( )
A.30° B.45°
C.50° D.60°
二、填空题:
13、圆内接正五边形ABCDE中,对角线AC和BD相交于点P,则∠APB的度数是 .
14、如图,圆O的内接正六边形的边长是12,则边心距是
15、如图,正六边形ABCDEF内接于半径为3的⊙O,则劣弧AB的长度为????? .
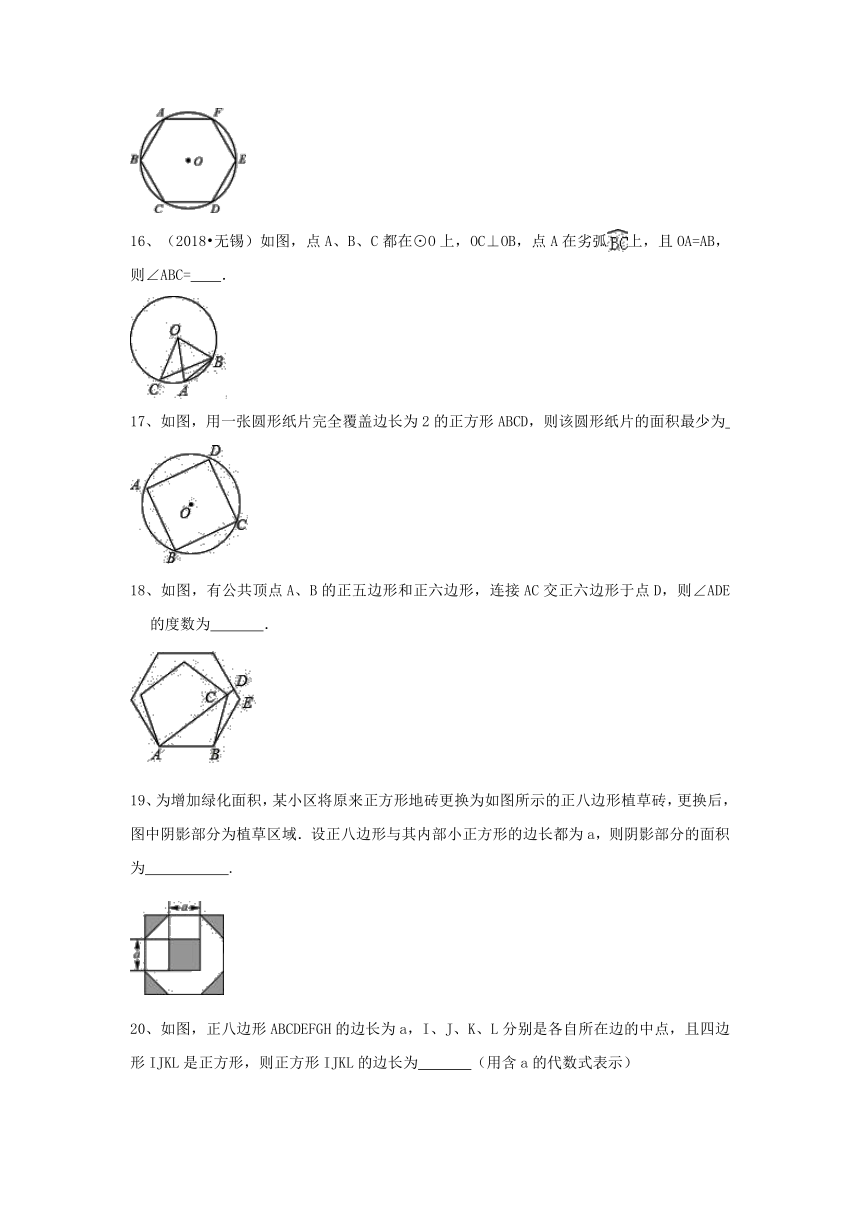
16、(2018?无锡)如图,点A、B、C都在⊙O上,OC⊥OB,点A在劣弧上,且OA=AB,则∠ABC= .
如图,用一张圆形纸片完全覆盖边长为2的正方形ABCD,则该圆形纸片的面积最少为
18、如图,有公共顶点A、B的正五边形和正六边形,连接AC交正六边形于点D,则∠ADE的度数为 .
19、为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域.设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为 .
如图,正八边形ABCDEFGH的边长为a,I、J、K、L分别是各自所在边的中点,且四边形IJKL是正方形,则正方形IJKL的边长为 (用含a的代数式表示)
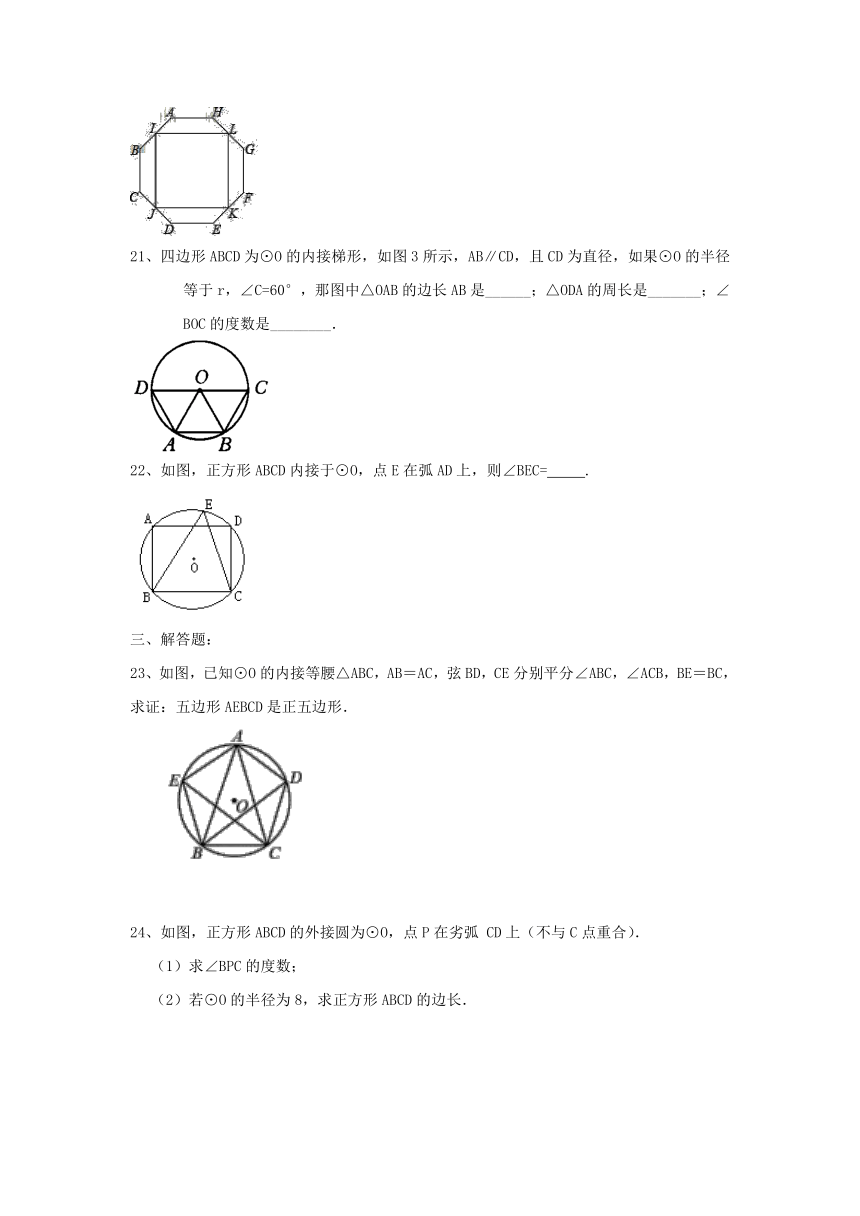
21、四边形ABCD为⊙O的内接梯形,如图3所示,AB∥CD,且CD为直径,如果⊙O的半径等于r,∠C=60°,那图中△OAB的边长AB是______;△ODA的周长是_______;∠BOC的度数是________.
22、如图,正方形ABCD内接于⊙O,点E在弧AD上,则∠BEC= .
三、解答题:
23、如图,已知⊙O的内接等腰△ABC,AB=AC,弦BD,CE分别平分∠ABC,∠ACB,BE=BC,求证:五边形AEBCD是正五边形.
24、如图,正方形ABCD的外接圆为⊙O,点P在劣弧 CD上(不与C点重合).
(1)求∠BPC的度数;
(2)若⊙O的半径为8,求正方形ABCD的边长.
25、如图,点G,H分别是正六边形ABCDEF的边BC,CD上的点,且BG=CH,AG交BH于点P.
(1)求证:ABG≌BCH;
(2)求∠APH的度数.
26、济南市实施“容貌工程”期间,某学校在教学楼前铺设小广场地面,其图案设计如图①,正方形小广场地面的边长是40米,中心建一个直径为20米的圆形花坛,四角各留一个边长为10米的小正方形花坛,种植高大树木,图中阴影处铺设广场砖.
(1)计算阴影部分的面积S(取3);
(2)某施工队承包铺设广场砖的任务,计划在一定时间内完成.按计划工作1天后,改进了铺设工艺,每天比原计划多铺60平方米,结果提前3天完成任务,那么原计划每天铺设多少平方米?
(3)图②表示广场中心的圆形花坛的平面图,准备在圆形花坛内种植6种不同颜色的花卉,为了美观,要使同色花卉集中在一起,并且各色花卉的种植面积相等.请你帮助设计出一种种植方案,并画在图②上.(不必说明方案,用尺规作图.不写作法,保留作图痕迹)
27、如图正方形ABCD内接于⊙O,E为CD任意一点,连接DE、AE.
(1)求∠AED的度数.[来源:学科网ZXXK]
(2)如图2,过点B作BF∥DE交⊙O于点F,连接AF,AF=1,AE=4,求DE的长度.
参考答案:
一、选择题:
1、C
2、A
3、D
4、B
5、B
6、C
7、A
8、C
9、A
10、C
11、C
12、B
二、填空题:
13、72°
14、6√3
15、π
16、15°
17、2π
18、84°
19、2a2
20、(2+√2)a/2.
21、r 3r 60°
22、45°
三、解答题:
23、在△ABC中,∵AB=AC,
∴∠ABC=∠ACB,
又∵BD,CE分别平分∠ABC,∠ACB,
∴∠ABD=∠DBC=∠ACE=∠ECB,
∴===,
又∵BE=BC,
∴=,即====,
∴点A,E,B,C,D把⊙O五等分,
∴五边形AEBCD是正五边形
25、(1)∵在正六边形ABCDEF中,
AB=BC,∠ABC=∠C=120°,
在△ABG与△BCH中
AB=BC,∠ABC=∠C=120°,BG=CH,
∴△ABG≌△BCH;
(2)由(1)知:ABG≌△BCH,
∴∠BAG=∠HBC,
∴∠BPG=∠ABG=120°,
∴∠APH=∠BPG=120°.
27、(1)如图1中,连接OA、OD.
∵四边形ABCD是正方形,
∴∠AOD=90°,
∴∠AED=∠AOD=45°.
(2)如图2中,连接CF、CE、CA,作DH⊥AE于H.
∵BF∥DE,AB∥CD,
∴∠ABF=∠CDE,
∵∠CFA=∠AEC=90°,
∴∠DEC=∠AFB=135°,
∵CD=AB,
∴△CDE≌△ABF,
∴AF=CE=1,
∴AC==,
∴AD=AC=,
∵∠DHE=90°,
∴∠HDE=∠HED=45°,
∴DH=HE,设DH=EH=x,
在Rt△ADH中,∵AD2=AH2+DH2,
∴=(4﹣x)2+x2,
解得x=或(舍弃),
∴DE=DH=
一、选择题:
1、如图所示,正六边形ABCDEF内接于⊙O,则∠ADB的度数是( ).
A.60° B.45° C.30° D.22.5°
2、正多边形的一边所对的中心角与它的一个外角的关系是( )
A.相等????????B.互余?????C.互补????D.互余或互补
3、正六边形的半径是6,则这个正六边形的面积为( )
A.24 B.54
C. D.
4、如图,正六边形ABCDEF内接于⊙O,若⊙O的半径为6,则阴影部分的面积为( )
A.12π??????B.6π? C.9π? D.18π
5、已知圆内接正三角形的面积为,则该圆的内接正六边形的边心距是( )
A.2 B.1 C. D.
6、如图,⊙O内切于正方形ABCD,边BC、DC上两点M、N,且MN是⊙O的切线,当△AMN的面积为4时,则⊙O的半径r是( )
A. B. C.2 D.
在△ABC中,∠ACB=90°,∠B=15°,以C为圆心,CA长为半径的圆交AB于D,如图所示,若AC=6,则AD的长为( ).
A.π??????B.6π? C.3π? D.1.5π
8、如图,要拧开一个边长为a=6 mm的正六边形螺帽,扳手张开的开口b至少为( )
A.6 mm B.12 mmC.6 mm D.4 mm
9、如图所示,△ABC为⊙O的内接三角形,AB=1,∠C=30°,则⊙O的内接正六边形的面积为( )
A.2??????B.6? C.9? D.3
10、如图,用一张圆形纸片完全覆盖边长为2的正方形ABCD,则该圆形纸片的面积最少为( )
A.π B. C.2π D.4π
11、如图,圆中有四条弦,每一条弦都将圆分割成面积比为的两个部分,若这些弦的交点恰是一个正方形的顶点,那么这个正方形的外接圆的面积与图中阴影部分面积的比值为( )
A.2π B. C.π D.2-π
12、如图,以正六边形ADHGFE的一边AD为边向外作正方形ABCD,则∠BED的度数为( )
A.30° B.45°
C.50° D.60°
二、填空题:
13、圆内接正五边形ABCDE中,对角线AC和BD相交于点P,则∠APB的度数是 .
14、如图,圆O的内接正六边形的边长是12,则边心距是
15、如图,正六边形ABCDEF内接于半径为3的⊙O,则劣弧AB的长度为????? .
16、(2018?无锡)如图,点A、B、C都在⊙O上,OC⊥OB,点A在劣弧上,且OA=AB,则∠ABC= .
如图,用一张圆形纸片完全覆盖边长为2的正方形ABCD,则该圆形纸片的面积最少为
18、如图,有公共顶点A、B的正五边形和正六边形,连接AC交正六边形于点D,则∠ADE的度数为 .
19、为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域.设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为 .
如图,正八边形ABCDEFGH的边长为a,I、J、K、L分别是各自所在边的中点,且四边形IJKL是正方形,则正方形IJKL的边长为 (用含a的代数式表示)
21、四边形ABCD为⊙O的内接梯形,如图3所示,AB∥CD,且CD为直径,如果⊙O的半径等于r,∠C=60°,那图中△OAB的边长AB是______;△ODA的周长是_______;∠BOC的度数是________.
22、如图,正方形ABCD内接于⊙O,点E在弧AD上,则∠BEC= .
三、解答题:
23、如图,已知⊙O的内接等腰△ABC,AB=AC,弦BD,CE分别平分∠ABC,∠ACB,BE=BC,求证:五边形AEBCD是正五边形.
24、如图,正方形ABCD的外接圆为⊙O,点P在劣弧 CD上(不与C点重合).
(1)求∠BPC的度数;
(2)若⊙O的半径为8,求正方形ABCD的边长.
25、如图,点G,H分别是正六边形ABCDEF的边BC,CD上的点,且BG=CH,AG交BH于点P.
(1)求证:ABG≌BCH;
(2)求∠APH的度数.
26、济南市实施“容貌工程”期间,某学校在教学楼前铺设小广场地面,其图案设计如图①,正方形小广场地面的边长是40米,中心建一个直径为20米的圆形花坛,四角各留一个边长为10米的小正方形花坛,种植高大树木,图中阴影处铺设广场砖.
(1)计算阴影部分的面积S(取3);
(2)某施工队承包铺设广场砖的任务,计划在一定时间内完成.按计划工作1天后,改进了铺设工艺,每天比原计划多铺60平方米,结果提前3天完成任务,那么原计划每天铺设多少平方米?
(3)图②表示广场中心的圆形花坛的平面图,准备在圆形花坛内种植6种不同颜色的花卉,为了美观,要使同色花卉集中在一起,并且各色花卉的种植面积相等.请你帮助设计出一种种植方案,并画在图②上.(不必说明方案,用尺规作图.不写作法,保留作图痕迹)
27、如图正方形ABCD内接于⊙O,E为CD任意一点,连接DE、AE.
(1)求∠AED的度数.[来源:学科网ZXXK]
(2)如图2,过点B作BF∥DE交⊙O于点F,连接AF,AF=1,AE=4,求DE的长度.
参考答案:
一、选择题:
1、C
2、A
3、D
4、B
5、B
6、C
7、A
8、C
9、A
10、C
11、C
12、B
二、填空题:
13、72°
14、6√3
15、π
16、15°
17、2π
18、84°
19、2a2
20、(2+√2)a/2.
21、r 3r 60°
22、45°
三、解答题:
23、在△ABC中,∵AB=AC,
∴∠ABC=∠ACB,
又∵BD,CE分别平分∠ABC,∠ACB,
∴∠ABD=∠DBC=∠ACE=∠ECB,
∴===,
又∵BE=BC,
∴=,即====,
∴点A,E,B,C,D把⊙O五等分,
∴五边形AEBCD是正五边形
25、(1)∵在正六边形ABCDEF中,
AB=BC,∠ABC=∠C=120°,
在△ABG与△BCH中
AB=BC,∠ABC=∠C=120°,BG=CH,
∴△ABG≌△BCH;
(2)由(1)知:ABG≌△BCH,
∴∠BAG=∠HBC,
∴∠BPG=∠ABG=120°,
∴∠APH=∠BPG=120°.
27、(1)如图1中,连接OA、OD.
∵四边形ABCD是正方形,
∴∠AOD=90°,
∴∠AED=∠AOD=45°.
(2)如图2中,连接CF、CE、CA,作DH⊥AE于H.
∵BF∥DE,AB∥CD,
∴∠ABF=∠CDE,
∵∠CFA=∠AEC=90°,
∴∠DEC=∠AFB=135°,
∵CD=AB,
∴△CDE≌△ABF,
∴AF=CE=1,
∴AC==,
∴AD=AC=,
∵∠DHE=90°,
∴∠HDE=∠HED=45°,
∴DH=HE,设DH=EH=x,
在Rt△ADH中,∵AD2=AH2+DH2,
∴=(4﹣x)2+x2,
解得x=或(舍弃),
∴DE=DH=
同课章节目录
