2.1.2 指数函数及其性质 课件41张PPT
文档属性
| 名称 | 2.1.2 指数函数及其性质 课件41张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-19 15:00:15 | ||
图片预览









文档简介
课件41张PPT。§2.1.2指数函数及其性质 复习学习函数的一般模式(方法):解析式(定义)图像性质应用数形结合分类讨论①定义域②值域③单调性④奇偶性⑤其它引入问题1、某种细胞分裂时,由1个分裂成
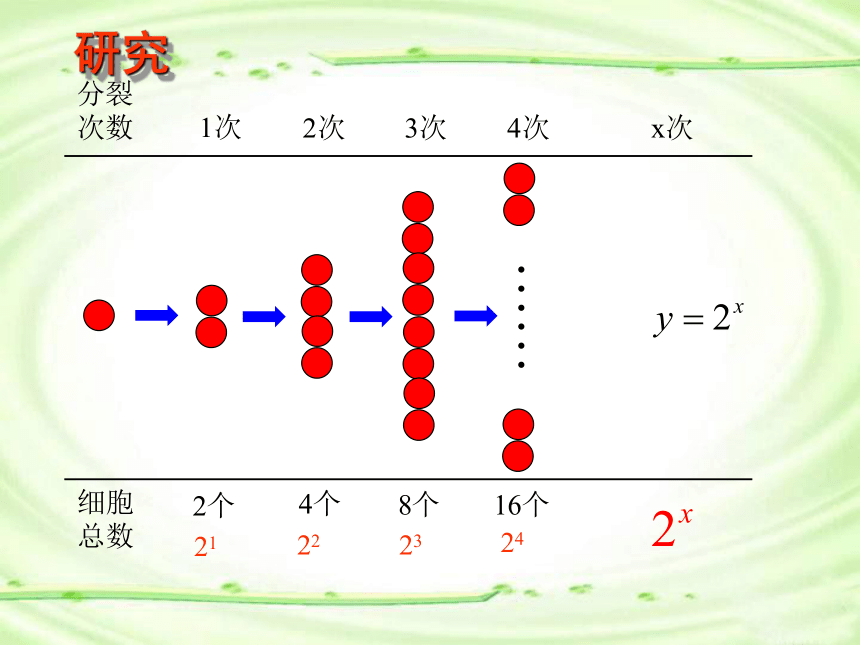
2个,2个分裂成4个,1个这样的细胞分
裂x次后,得到的细胞个数y与x的函数
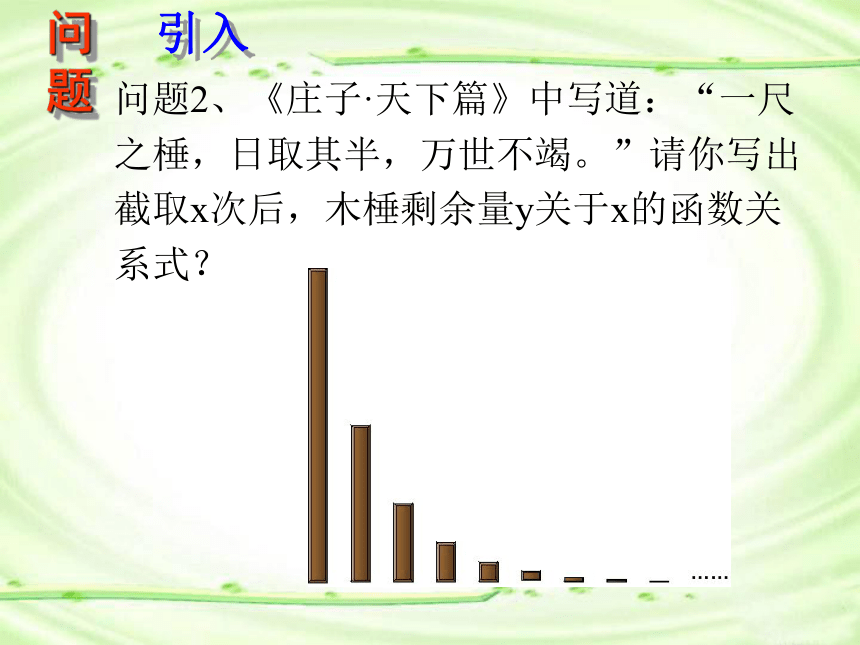
关系式是什么?问题21222324研究引入问题2、《庄子·天下篇》中写道:“一尺
之棰,日取其半,万世不竭。”请你写出
截取x次后,木棰剩余量y关于x的函数关
系式?问题研究提炼 思考 (1)为什么定义域为R?
(2)为什么规定底数a >0且a ≠1呢? 认识(口答)判断下列函数是不是指 数函数,为什么?√√例题③ ( )① ②且④ ⑤ ⑥ ⑦ ⑧√ 已知指数函数 的图像经过点 求 的值.分析:指数函数的图象经过点 , 有 ,
即 ,解得
于是有思考:确定一个指数函数需要什么条件?想一想例题所以:设问2:得到函数的图象一般用什么方法?列表、描点、连线作图在同一坐标系中画出下列四个函数的图象:
(1)y=2x (2)y=(1/2)x
(3)y=3x (4)y=(1/3)x 87654321-6-4-224687654321-6-4-224687654321-6-4-2246F:指数函数性质图象.rar 图 象 性 质yx0y=1(0,1)y=ax
(a>1)yx(0,1)y=10y=ax
(010 0 时,y > 1.
当 x < 0 时,. 0< y < 1
当 x < 0 时,y > 1;
当 x > 0 时, 0< y < 1。底互为倒数的两个函数图像关于y轴对称 在第一象限沿箭头方向底增大深入探究 你还能发现指数函数图象和底数的关系吗?1、求下列函数的定义域和值域:应用分析:注意应用指数函数的定义域和单调性.【变式训练】若函数y=(a2-3a+3)·ax是指数函数,则实数a=______.
【解析】由y=(a2-3a+3)·ax是指数函数可得
解得
即a=2.
答案:2【例】函数y=ax+2(a>0且a≠1)的图象过定点P,则点P的坐标是______.
【规范解答】当x+2=0,
即x=-2时,y=a-2+2=1,
∴P(-2,1).
答案:(-2,1)
【例3】求下列函数的定义域和值域:
(1) (2)
【审题指导】此类问题可先由所给函数的形式求其定义域,而求函数值域时应考虑指数函数y=ax(a>0,a≠1)的值域,并结合函数自身特征,利用单调性处理.【规范解答】(1)x应满足x-4≠0,∴x≠4,
∴函数定义域为{x∈R|x≠4}.
∵x≠4,∴x-4≠0,
∴y= 的值域为{y|y>0,y≠1}.(2)定义域为R.
∵|x|≥0,
∴y=
∴值域是{y|y≥1}.
【规范解答】(1)x应满足x-4≠0,∴x≠4,
∴函数定义域为{x∈R|x≠4}.
∵x≠4,∴x-4≠0,
∴y= 的值域为{y|y>0,y≠1}.
(2)定义域为R.
∵|x|≥0,
∴y=
∴值域是{y|y≥1}.
2、比较下列各题中两个值的大小:
分析: (1)(2)利用指数函数的单调性.
(3) 找中间量是关键.应用 ∵函数 在R上是增函数,
而指数2.5<3.(1)应用<解:应用(2) ∵函数 在R上是减函数,
而指数-0.1>-0.2解:∴<应用(3)解:根据指数函数的性质,得:且从而有比较下列各题中两个值的大小:应用 方法总结:
对同底数幂大小的比较用的是指数函数的单调性,必须要明确所给的两个值是哪个指数函数的两个函数值;对不同底数幂的大小的比较可以与中间值进行比较. 例2:已知下列不等式 , 比较 m,n 的大小 :
(1)
(2)
(3) 知识的逆用,建立函数思想和分类讨论思想双基训练,知识内化5.不等式0.52x>0.5x-1的解集为______(用区间表示).
【解析】∵y=0.5x在R上单调递减,
又0.52x>0.5x-1,∴2x 答案:(-∞,-1)1.下列函数中一定是指数函数的是( )
2.已知
则 的大小关系是____________.
练习Ca>b>c2.下列函数是指数函数的是( )
(A)y=(-2)x (B)y=x3
(C)y=-2x (D)y=2x
【解析】选D.判断一个函数是否是指数函数,关键看它是否符合指数函数的结构特征,比较选项可知D正确.练习3.指数函数y=ax与y=bx的图象如图,则( )
(A)a<0,b<0
(B)a<0,b>0
(C)01
(D)0【解析】选C.指数函数在底数大于1时单调递增,底数大于0小于1时单调递减,因而选C.
2.已知0(A)第一象限 (B)第二象限
(C)第三象限 (D)第四象限
【解析】选A.∵0【解析】由题意可知,0<2-a<1,即1答案:1【解析】设指数函数是y=ax(a>0,a≠1),则有
8=a3,∴a=2,∴y=2x.
从而f(4)=24=16,f(-4)=2-4= 6.已知 求函数y=2x的值域.
【解析】由 得22x≤24-2x,
∴2x≤4-2x,解得x≤1,∴0<2x≤21=2,
∴函数的值域是(0,2].D点滴收获:
1. 本节课学习了那些知识?指数函数的定义2.如何记忆函数的性质?指数函数的图象及性质数形结合的方法记忆3.记住两个基本图形:
2个,2个分裂成4个,1个这样的细胞分
裂x次后,得到的细胞个数y与x的函数
关系式是什么?问题21222324研究引入问题2、《庄子·天下篇》中写道:“一尺
之棰,日取其半,万世不竭。”请你写出
截取x次后,木棰剩余量y关于x的函数关
系式?问题研究提炼 思考 (1)为什么定义域为R?
(2)为什么规定底数a >0且a ≠1呢? 认识(口答)判断下列函数是不是指 数函数,为什么?√√例题③ ( )① ②且④ ⑤ ⑥ ⑦ ⑧√ 已知指数函数 的图像经过点 求 的值.分析:指数函数的图象经过点 , 有 ,
即 ,解得
于是有思考:确定一个指数函数需要什么条件?想一想例题所以:设问2:得到函数的图象一般用什么方法?列表、描点、连线作图在同一坐标系中画出下列四个函数的图象:
(1)y=2x (2)y=(1/2)x
(3)y=3x (4)y=(1/3)x 87654321-6-4-224687654321-6-4-224687654321-6-4-2246F:指数函数性质图象.rar 图 象 性 质yx0y=1(0,1)y=ax
(a>1)yx(0,1)y=10y=ax
(0
当 x < 0 时,. 0< y < 1
当 x < 0 时,y > 1;
当 x > 0 时, 0< y < 1。底互为倒数的两个函数图像关于y轴对称 在第一象限沿箭头方向底增大深入探究 你还能发现指数函数图象和底数的关系吗?1、求下列函数的定义域和值域:应用分析:注意应用指数函数的定义域和单调性.【变式训练】若函数y=(a2-3a+3)·ax是指数函数,则实数a=______.
【解析】由y=(a2-3a+3)·ax是指数函数可得
解得
即a=2.
答案:2【例】函数y=ax+2(a>0且a≠1)的图象过定点P,则点P的坐标是______.
【规范解答】当x+2=0,
即x=-2时,y=a-2+2=1,
∴P(-2,1).
答案:(-2,1)
【例3】求下列函数的定义域和值域:
(1) (2)
【审题指导】此类问题可先由所给函数的形式求其定义域,而求函数值域时应考虑指数函数y=ax(a>0,a≠1)的值域,并结合函数自身特征,利用单调性处理.【规范解答】(1)x应满足x-4≠0,∴x≠4,
∴函数定义域为{x∈R|x≠4}.
∵x≠4,∴x-4≠0,
∴y= 的值域为{y|y>0,y≠1}.(2)定义域为R.
∵|x|≥0,
∴y=
∴值域是{y|y≥1}.
【规范解答】(1)x应满足x-4≠0,∴x≠4,
∴函数定义域为{x∈R|x≠4}.
∵x≠4,∴x-4≠0,
∴y= 的值域为{y|y>0,y≠1}.
(2)定义域为R.
∵|x|≥0,
∴y=
∴值域是{y|y≥1}.
2、比较下列各题中两个值的大小:
分析: (1)(2)利用指数函数的单调性.
(3) 找中间量是关键.应用 ∵函数 在R上是增函数,
而指数2.5<3.(1)应用<解:应用(2) ∵函数 在R上是减函数,
而指数-0.1>-0.2解:∴<应用(3)解:根据指数函数的性质,得:且从而有比较下列各题中两个值的大小:应用 方法总结:
对同底数幂大小的比较用的是指数函数的单调性,必须要明确所给的两个值是哪个指数函数的两个函数值;对不同底数幂的大小的比较可以与中间值进行比较. 例2:已知下列不等式 , 比较 m,n 的大小 :
(1)
(2)
(3) 知识的逆用,建立函数思想和分类讨论思想双基训练,知识内化5.不等式0.52x>0.5x-1的解集为______(用区间表示).
【解析】∵y=0.5x在R上单调递减,
又0.52x>0.5x-1,∴2x
2.已知
则 的大小关系是____________.
练习Ca>b>c2.下列函数是指数函数的是( )
(A)y=(-2)x (B)y=x3
(C)y=-2x (D)y=2x
【解析】选D.判断一个函数是否是指数函数,关键看它是否符合指数函数的结构特征,比较选项可知D正确.练习3.指数函数y=ax与y=bx的图象如图,则( )
(A)a<0,b<0
(B)a<0,b>0
(C)0
(D)0
2.已知0
(C)第三象限 (D)第四象限
【解析】选A.∵0
8=a3,∴a=2,∴y=2x.
从而f(4)=24=16,f(-4)=2-4= 6.已知 求函数y=2x的值域.
【解析】由 得22x≤24-2x,
∴2x≤4-2x,解得x≤1,∴0<2x≤21=2,
∴函数的值域是(0,2].D点滴收获:
1. 本节课学习了那些知识?指数函数的定义2.如何记忆函数的性质?指数函数的图象及性质数形结合的方法记忆3.记住两个基本图形:
