指数函数及其性质 课件28张PPT
文档属性
| 名称 | 指数函数及其性质 课件28张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 900.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-19 15:06:05 | ||
图片预览






文档简介
课件28张PPT。2018/11/191(第一课时)出处:人教版高一数学必修一2教学目标
◆理解指数函数的概念和意义.
◆初步掌握指数函数的有关性质.能画出具体的
指数函数图像
【重点】指数函数的概念和意义
指数函数的图像和性质
【难点】指数函数图象和性质的应用.
【教法】观察法、讨论法及讲授法
【学法 】归纳-------讨论-------练习
【教学手段】多媒体电脑与投影仪
【 数学思想】数形结合的思想
3课前小实验对折纸课前准备4课前小实验
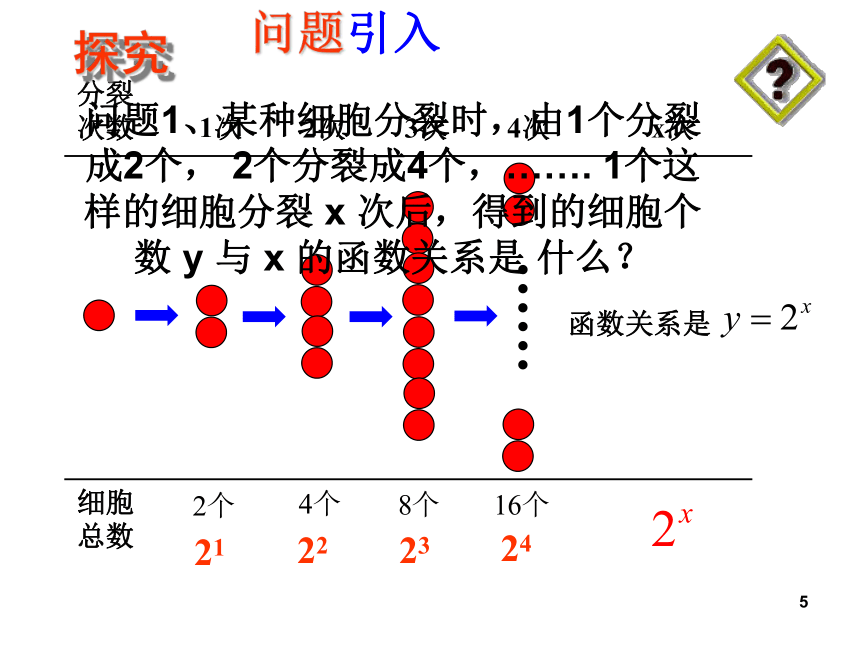
对折绳子课前准备521222324探究问题引入问题1、某种细胞分裂时,由1个分裂成2个, 2个分裂成4个,……. 1个这样的细胞分裂 x 次后,得到的细胞个数 y 与 x 的函数关系是 什么?函数关系是6引入问题2、《庄子·天下篇》中写道:“一尺
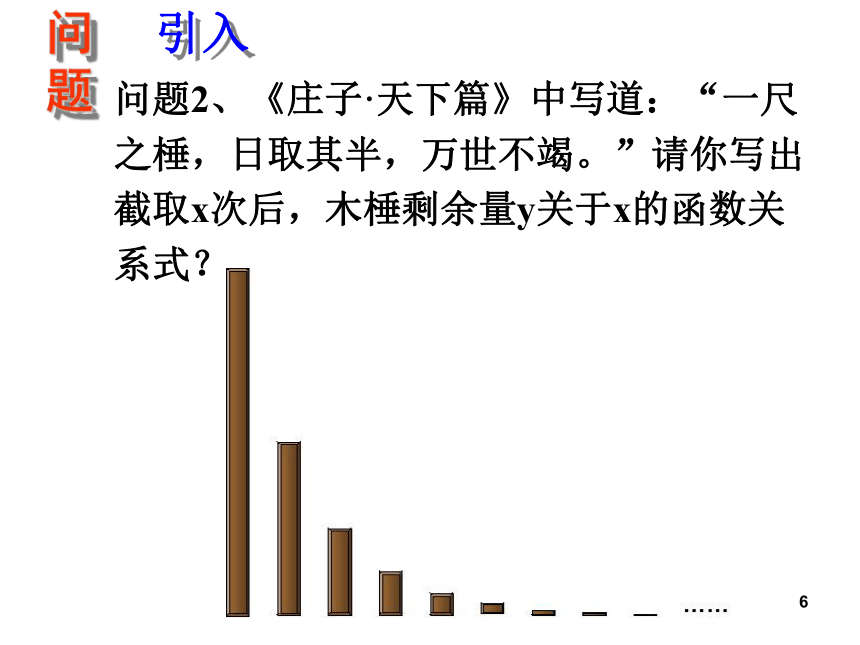
之棰,日取其半,万世不竭。”请你写出
截取x次后,木棰剩余量y关于x的函数关
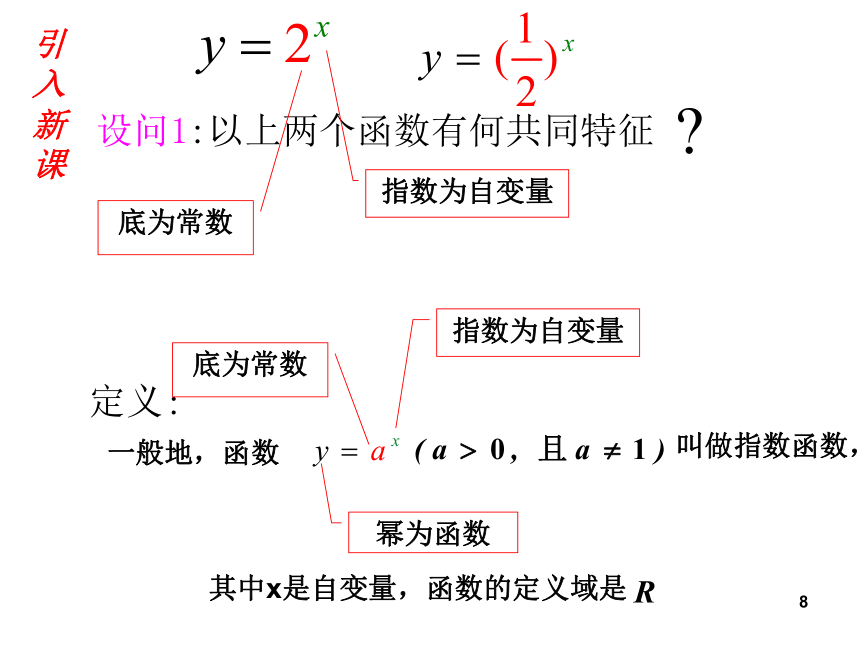
系式?问题7探究函数关系是8指数为自变量底为常数引入新课
9一、指数函数的定义叫做指数函数,是自变量,函数的定义域是R一般地,函数其中问题:为什么要规定a>0,且a1呢?1011注意:要判断一个函数是否是指数函数,需抓住三点:
⑴底数a是大于0且不等于1的常数;
⑵自变量 在指数位置;指数是单个的x
⑶ 的系数必须为1;且没有其他的项.
如 不是指数函数
叫做指数函数,是自变量,一般地,函数其中函数的定义域是R我不是12我是例1、下列函数中,哪些是指数函数?我是我不是口答且①②③④⑤⑥⑦⑧我不是为什么?你答对了吗?13练习、函数y=(a2-3a+3)ax是指数函数,则a= ____ 例2、已知指数函数 的图象经过点 ,求 的值。2思考:确定一个指数函数需要什么条件?所以解:因为f(x)=ax的图像经过点(3,),所以
f(3)= 即 ,解得 ,
于是二、指数函数图像和性质 设问:怎样得到指数函数图像?
得到函数的图象一般用什么方法?
指数函数图像的特点?
在同一坐标系中画出y=2x和y= 的大致图
像,并说出这两个函数的性质1587654321-6-4-224687654321-6-4-224687654321-6-4-2246171819通过图像,你能发现指数函数的哪 些性质?●●20 图 象 性 质yx0y=1(0,1)y=ax
(a>1)yx(0,1)y=10y=ax
(010 0 时,y > 1.
当 x < 0 时,. 0< y < 1
当 x < 0 时,y > 1;
当 x > 0 时, 0< y < 1。在第一象限沿箭头方向底增大21三、深入探究,加深理解 观察图像,发现图像与底的关系底互为倒数的两个函数图像关于y轴对称 在y轴的右侧,图像从下到上相应的底数由小变大大小22 例3:求下列函数的定义域
(1) (2)
(3) (4)小结:函数 的定义域与
的定义域为相同解(1)要使函数有意义,必须 即
所以函数的定义域为求 型函数的定义域时,往往转化为
解指数不等式(组)、23例4:比较下列各题中两个值的大小:①,; 同底比较大小24 ②, 同底指数幂比大小,构造指数函数,利用函数单调性 同底比较大小25 ③,底不同,指数也不同 利用函数图像或中间变量进行比较 不同底数幂比大小,利用指数函数图像与底的关系比较26四、当堂训练,共同提高(1)1.52.5 , 1.53; (2) 0.6-01,0.6-02 比较下列各题中两值的大小(6)0.8-0.3与 ,4.9-0.1底不同,指数也不同>(5)(0.3) -0.3 与 (0.2) -0.3 不同底但同指数(3) (4) 与不同底但可化同底同底比较大小<<<<> 同底指数幂比大小,构造指数函数,利用函数 的单调性 利用函数图像或中间变量进行比较常用1和0.
27五、小结归纳:点滴收获
1. 本节课学习了那些知识?指数函数的定义2.如何记忆函数的性质?指数函数的图象及性质数形结合的方法记忆3.记住两个基本图形:必做题课本P21习题2.1
A组5,6 ,7题
选做题优化探究双击自测
和学以致用1,2六、布置作业,28谢谢大家
◆初步掌握指数函数的有关性质.能画出具体的
指数函数图像
【重点】指数函数的概念和意义
指数函数的图像和性质
【难点】指数函数图象和性质的应用.
【教法】观察法、讨论法及讲授法
【学法 】归纳-------讨论-------练习
【教学手段】多媒体电脑与投影仪
【 数学思想】数形结合的思想
3课前小实验对折纸课前准备4课前小实验
对折绳子课前准备521222324探究问题引入问题1、某种细胞分裂时,由1个分裂成2个, 2个分裂成4个,……. 1个这样的细胞分裂 x 次后,得到的细胞个数 y 与 x 的函数关系是 什么?函数关系是6引入问题2、《庄子·天下篇》中写道:“一尺
之棰,日取其半,万世不竭。”请你写出
截取x次后,木棰剩余量y关于x的函数关
系式?问题7探究函数关系是8指数为自变量底为常数引入新课
9一、指数函数的定义叫做指数函数,是自变量,函数的定义域是R一般地,函数其中问题:为什么要规定a>0,且a1呢?1011注意:要判断一个函数是否是指数函数,需抓住三点:
⑴底数a是大于0且不等于1的常数;
⑵自变量 在指数位置;指数是单个的x
⑶ 的系数必须为1;且没有其他的项.
如 不是指数函数
叫做指数函数,是自变量,一般地,函数其中函数的定义域是R我不是12我是例1、下列函数中,哪些是指数函数?我是我不是口答且①②③④⑤⑥⑦⑧我不是为什么?你答对了吗?13练习、函数y=(a2-3a+3)ax是指数函数,则a= ____ 例2、已知指数函数 的图象经过点 ,求 的值。2思考:确定一个指数函数需要什么条件?所以解:因为f(x)=ax的图像经过点(3,),所以
f(3)= 即 ,解得 ,
于是二、指数函数图像和性质 设问:怎样得到指数函数图像?
得到函数的图象一般用什么方法?
指数函数图像的特点?
在同一坐标系中画出y=2x和y= 的大致图
像,并说出这两个函数的性质1587654321-6-4-224687654321-6-4-224687654321-6-4-2246171819通过图像,你能发现指数函数的哪 些性质?●●20 图 象 性 质yx0y=1(0,1)y=ax
(a>1)yx(0,1)y=10y=ax
(0
当 x < 0 时,. 0< y < 1
当 x < 0 时,y > 1;
当 x > 0 时, 0< y < 1。在第一象限沿箭头方向底增大21三、深入探究,加深理解 观察图像,发现图像与底的关系底互为倒数的两个函数图像关于y轴对称 在y轴的右侧,图像从下到上相应的底数由小变大大小22 例3:求下列函数的定义域
(1) (2)
(3) (4)小结:函数 的定义域与
的定义域为相同解(1)要使函数有意义,必须 即
所以函数的定义域为求 型函数的定义域时,往往转化为
解指数不等式(组)、23例4:比较下列各题中两个值的大小:①,; 同底比较大小24 ②, 同底指数幂比大小,构造指数函数,利用函数单调性 同底比较大小25 ③,底不同,指数也不同 利用函数图像或中间变量进行比较 不同底数幂比大小,利用指数函数图像与底的关系比较26四、当堂训练,共同提高(1)1.52.5 , 1.53; (2) 0.6-01,0.6-02 比较下列各题中两值的大小(6)0.8-0.3与 ,4.9-0.1底不同,指数也不同>(5)(0.3) -0.3 与 (0.2) -0.3 不同底但同指数(3) (4) 与不同底但可化同底同底比较大小<<<<> 同底指数幂比大小,构造指数函数,利用函数 的单调性 利用函数图像或中间变量进行比较常用1和0.
27五、小结归纳:点滴收获
1. 本节课学习了那些知识?指数函数的定义2.如何记忆函数的性质?指数函数的图象及性质数形结合的方法记忆3.记住两个基本图形:必做题课本P21习题2.1
A组5,6 ,7题
选做题优化探究双击自测
和学以致用1,2六、布置作业,28谢谢大家
