指数函数及其性质课件28张PPT
图片预览







文档简介
课件28张PPT。 第二章 基本初等函数(一)2.1.2 指数函数及其性质一、情境引入猜想:如果给你足够大的一张纸,让你对折51次,你能说出折叠后的厚度吗? 用计算机可以算出来这道简单的数学题。2的51次方=2251799813685248,如果这张纸的厚度按照0.07毫米计算,那么对折51次后它的结果就是1.576多亿公里,超过了地球到太阳的1.496亿公里的距离! 一页纸折叠x次后,得到的纸的页数y与 x的函数关系式是 y=2 x 次数 页数1次 2 页2次 2×2=2 2 页3次 2 2 ×2=2 3 页4次 2 3×2=2 4页
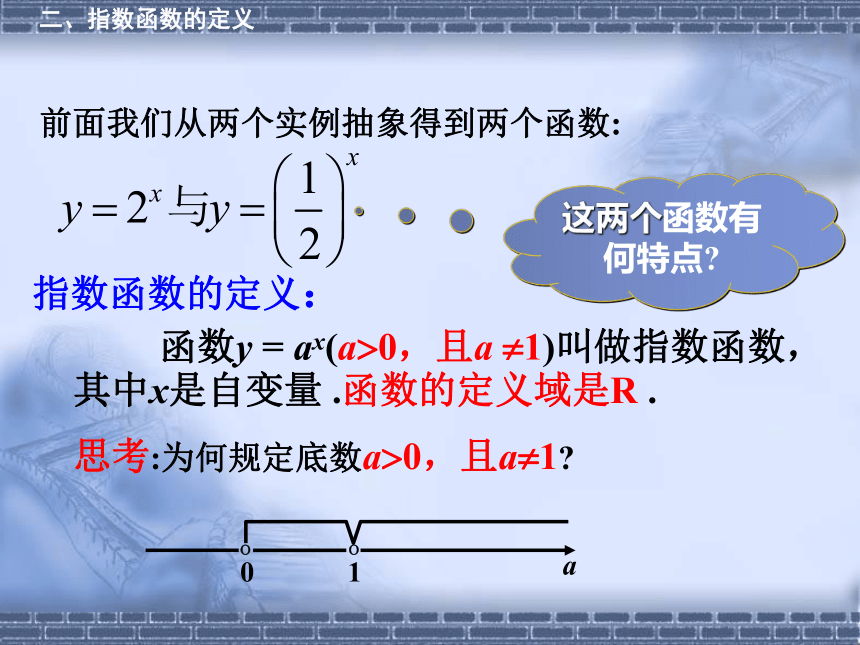
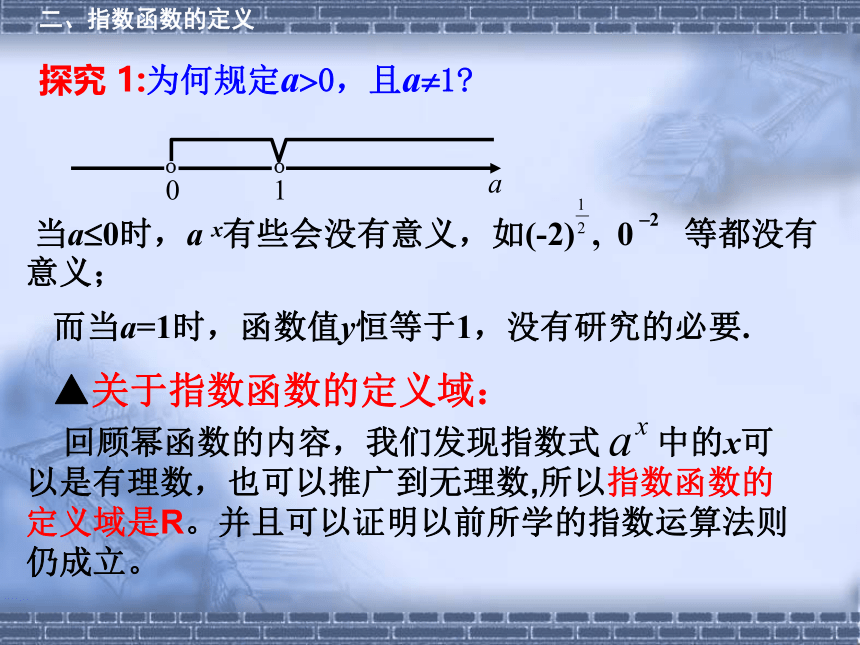
x次 2 (x-1) ×2=2x页一、情境引入情景2 .有一个同学喝水的时候,第一次喝掉杯中的一半,第二次喝掉剩余部分的一半,第三次喝掉第二次剩余部分的一半,依次下去,问喝水的次数x与杯中剩余水的容量y之间的函数关系如何?(假设原来水容量为1个单位)……一、情境引入二、指数函数的定义前面我们从两个实例抽象得到两个函数:指数函数的定义:这两个函数有何特点? 函数y = ax(a?0,且a ?1)叫做指数函数,其中x是自变量 .函数的定义域是R .思考:为何规定底数a?0,且a?1? 当a?0时,a x有些会没有意义,如(-2) , 0 等都没有意义;而当a=1时,函数值y恒等于1,没有研究的必要.探究 1:为何规定a?0,且a?1?▲关于指数函数的定义域: 回顾幂函数的内容,我们发现指数式 中的x可以是有理数,也可以推广到无理数,所以指数函数的定义域是R。并且可以证明以前所学的指数运算法则仍成立。二、指数函数的定义探究2:函数是指数函数吗?不是。因为指数函数的解析式y=中,的系数是1.指数函数的解析式 ,
的系数是1 ;
指数必须是单个x ;
底数是常量a?0,且a?1.特点:二、指数函数的定义(1)y=2x +1
(2)y=3·4x (x∈R) (3)y=3x (x∈R)
(4)y=10-x (5)y=(-2)x (x∈R)
(6)y= 2x+11.下列哪些是指数函数?练一练例1 已知指数函数
的图象经过点 ,求f(0), f(1), f(-3)。用图像法探究指数函数的图像和性质: 在坐标系中分别作出函数的图象.作图的基本步骤:
列表、描点、连线。三、图像与性质三、图像与性质观察李琪琪同学做的图象,回答下列问题:问题一:
图象分别在哪几个象限?问题二:
图象的上升、下降与底数a有联系吗?问题三:
图象中有哪些特殊的点?答:两个图象都在第____象限答:当底数__时图象上升;当底数____时图象下降.答:两个图象都经过点____.Ⅰ、Ⅱ三、图像与性质011011三、图像与性质三、图像与性质 图 象 性 质yx0y=1(0,1)y=ax
(a>1)yx(0,1)y=10y=ax
(010(a>1)yx(0,1)y=10y=ax
(010 1;
当 x > 0 时, 0< y < 1。当 x > 0 时,y > 1.
当 x < 0 时,. 0< y < 1
三、图像与性质 图 象 性 质yx0y=1(0,1)y=ax
(a>1)yx(0,1)y=10y=ax
(010
(1)1.72.5 , 1.73 ;
考查函数 y=因为1.7>1,所以函数y=<解① :利用函数单调性在R上是增函数,而2.5<3,
所以,数缺形时少直观三、图像与性质 ②, 解② :利用函数单调性考查函数 y= 因为0<0.8<1,所以函数y=在R是减函数, 而-0.1>-0.2,< 所以,数缺形时少直观三、图像与性质 ③,解③ :根据指数函数的性质,得且>从而有数缺形时少直观三、图像与性质例2. 比较下列各题中两个值的大小:
(1)1.72.5 , 1.73 ; (2)0.8-0.1 ,0.8 -0.2
(3)1.70.3 , 0.93.1.
小结 比较指数幂大小的方法:①、单调性法:利用函数的单调性,数的特征
是底同指不同(包括可以化为同底的)。②、中间值法:找一个 “中间值”如“1”来过渡,
数的特征是底不同指不同。三、图像与性质变式1. 比较大小:
(1)3.10.5 , 3.12.3
(2)
(3) 2.3-2.5 , 0.2 -0.1
<<>变式2 若a-2 > a-3,则a∈_________,若2m < 2n,则m_____n,
若( )m >2, 则m∈_______( 1,+∞ )<(-∞,-1)三、图像与性质探究3 观察图像,思考图像特征与底的关系?在第一象限沿箭头方向底增大比较大小
0.50.5 ;20.5四、探索与创新4.指数函数图像与性质的应用: 三、图像与性质三、课堂小结1、指数函数概念; 2、指数函数的图像与性质; 见图表 函数y = ax(a?0,且a ?1)叫做指数函数,其中x是自变量 .函数的定义域是R . 图 象 性 质yx0y=1(0,1)y=ax
(a>1)yx(0,1)y=10y=ax
(010 利用函数图像研究函数性质是一种直观而形象的方法,记忆指数函数性质时可以联想它的图像。数形结合思想 四、布置作业:
1、注意时间进行“过电影”。
2、伴你学:3.1.2 基础过关,第一课时。
3、课本P93 习题A,1、2、3
x次 2 (x-1) ×2=2x页一、情境引入情景2 .有一个同学喝水的时候,第一次喝掉杯中的一半,第二次喝掉剩余部分的一半,第三次喝掉第二次剩余部分的一半,依次下去,问喝水的次数x与杯中剩余水的容量y之间的函数关系如何?(假设原来水容量为1个单位)……一、情境引入二、指数函数的定义前面我们从两个实例抽象得到两个函数:指数函数的定义:这两个函数有何特点? 函数y = ax(a?0,且a ?1)叫做指数函数,其中x是自变量 .函数的定义域是R .思考:为何规定底数a?0,且a?1? 当a?0时,a x有些会没有意义,如(-2) , 0 等都没有意义;而当a=1时,函数值y恒等于1,没有研究的必要.探究 1:为何规定a?0,且a?1?▲关于指数函数的定义域: 回顾幂函数的内容,我们发现指数式 中的x可以是有理数,也可以推广到无理数,所以指数函数的定义域是R。并且可以证明以前所学的指数运算法则仍成立。二、指数函数的定义探究2:函数是指数函数吗?不是。因为指数函数的解析式y=中,的系数是1.指数函数的解析式 ,
的系数是1 ;
指数必须是单个x ;
底数是常量a?0,且a?1.特点:二、指数函数的定义(1)y=2x +1
(2)y=3·4x (x∈R) (3)y=3x (x∈R)
(4)y=10-x (5)y=(-2)x (x∈R)
(6)y= 2x+11.下列哪些是指数函数?练一练例1 已知指数函数
的图象经过点 ,求f(0), f(1), f(-3)。用图像法探究指数函数的图像和性质: 在坐标系中分别作出函数的图象.作图的基本步骤:
列表、描点、连线。三、图像与性质三、图像与性质观察李琪琪同学做的图象,回答下列问题:问题一:
图象分别在哪几个象限?问题二:
图象的上升、下降与底数a有联系吗?问题三:
图象中有哪些特殊的点?答:两个图象都在第____象限答:当底数__时图象上升;当底数____时图象下降.答:两个图象都经过点____.Ⅰ、Ⅱ三、图像与性质011011三、图像与性质三、图像与性质 图 象 性 质yx0y=1(0,1)y=ax
(a>1)yx(0,1)y=10y=ax
(0
(0
当 x > 0 时, 0< y < 1。当 x > 0 时,y > 1.
当 x < 0 时,. 0< y < 1
三、图像与性质 图 象 性 质yx0y=1(0,1)y=ax
(a>1)yx(0,1)y=10y=ax
(0
(1)1.72.5 , 1.73 ;
考查函数 y=因为1.7>1,所以函数y=<解① :利用函数单调性在R上是增函数,而2.5<3,
所以,数缺形时少直观三、图像与性质 ②, 解② :利用函数单调性考查函数 y= 因为0<0.8<1,所以函数y=在R是减函数, 而-0.1>-0.2,< 所以,数缺形时少直观三、图像与性质 ③,解③ :根据指数函数的性质,得且>从而有数缺形时少直观三、图像与性质例2. 比较下列各题中两个值的大小:
(1)1.72.5 , 1.73 ; (2)0.8-0.1 ,0.8 -0.2
(3)1.70.3 , 0.93.1.
小结 比较指数幂大小的方法:①、单调性法:利用函数的单调性,数的特征
是底同指不同(包括可以化为同底的)。②、中间值法:找一个 “中间值”如“1”来过渡,
数的特征是底不同指不同。三、图像与性质变式1. 比较大小:
(1)3.10.5 , 3.12.3
(2)
(3) 2.3-2.5 , 0.2 -0.1
<<>变式2 若a-2 > a-3,则a∈_________,若2m < 2n,则m_____n,
若( )m >2, 则m∈_______( 1,+∞ )<(-∞,-1)三、图像与性质探究3 观察图像,思考图像特征与底的关系?在第一象限沿箭头方向底增大比较大小
0.50.5 ;20.5四、探索与创新4.指数函数图像与性质的应用: 三、图像与性质三、课堂小结1、指数函数概念; 2、指数函数的图像与性质; 见图表 函数y = ax(a?0,且a ?1)叫做指数函数,其中x是自变量 .函数的定义域是R . 图 象 性 质yx0y=1(0,1)y=ax
(a>1)yx(0,1)y=10y=ax
(0
1、注意时间进行“过电影”。
2、伴你学:3.1.2 基础过关,第一课时。
3、课本P93 习题A,1、2、3
