1.3.1 单调性与最大(小)值25张PPT
文档属性
| 名称 | 1.3.1 单调性与最大(小)值25张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 576.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-19 00:00:00 | ||
图片预览


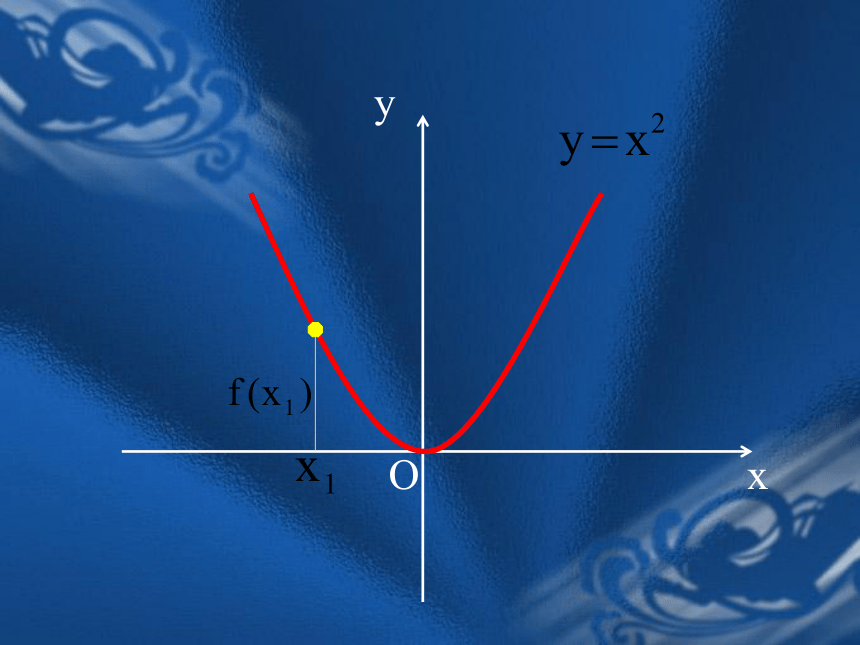
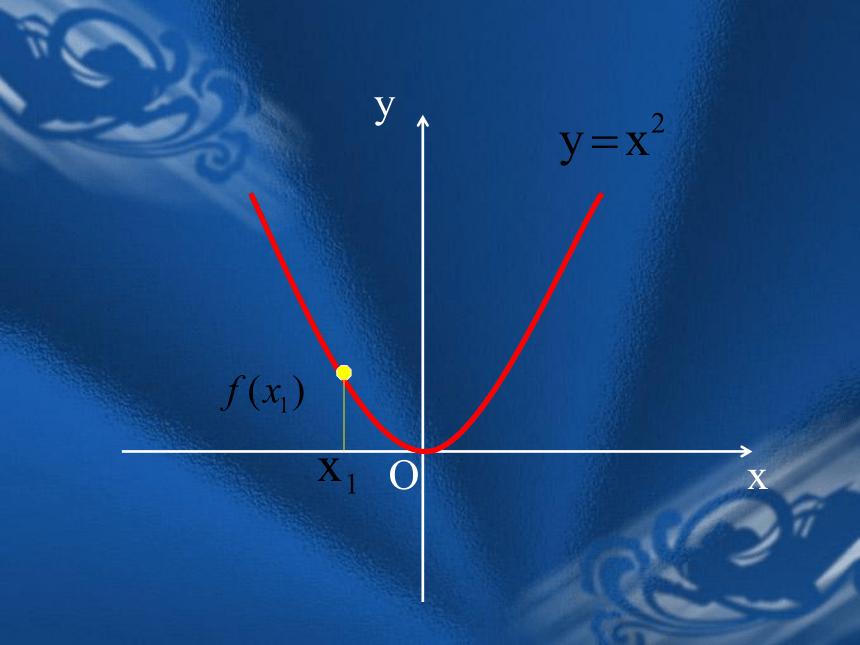
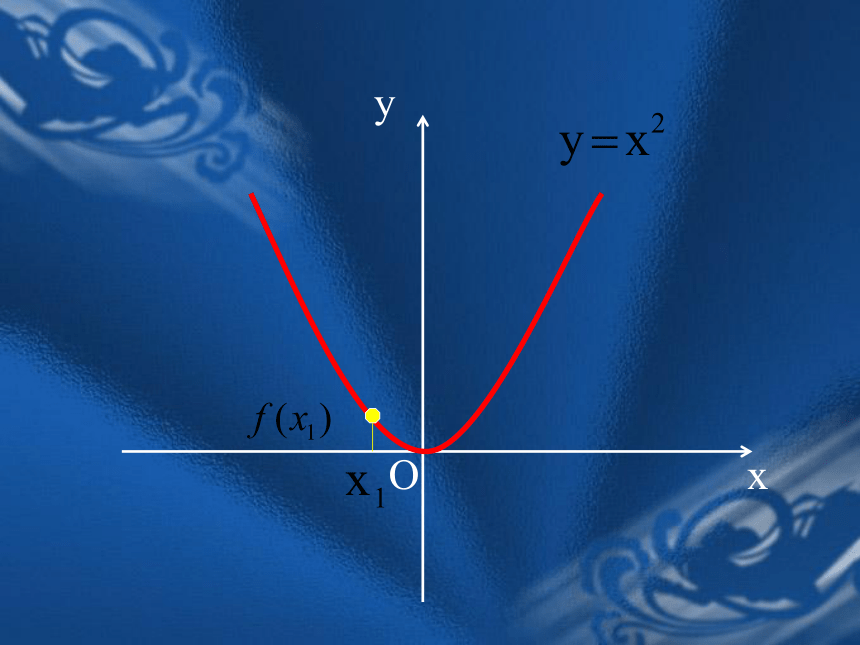
文档简介
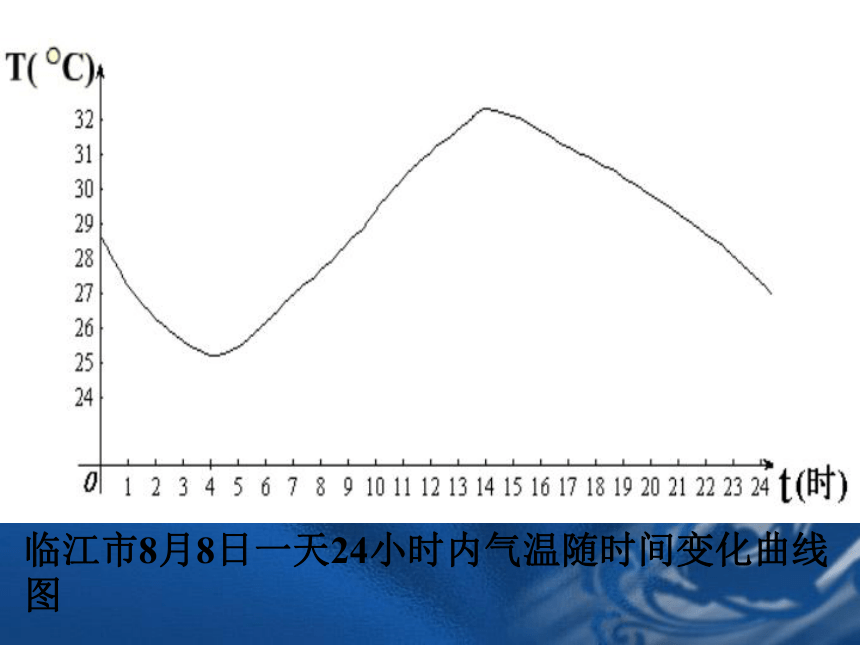
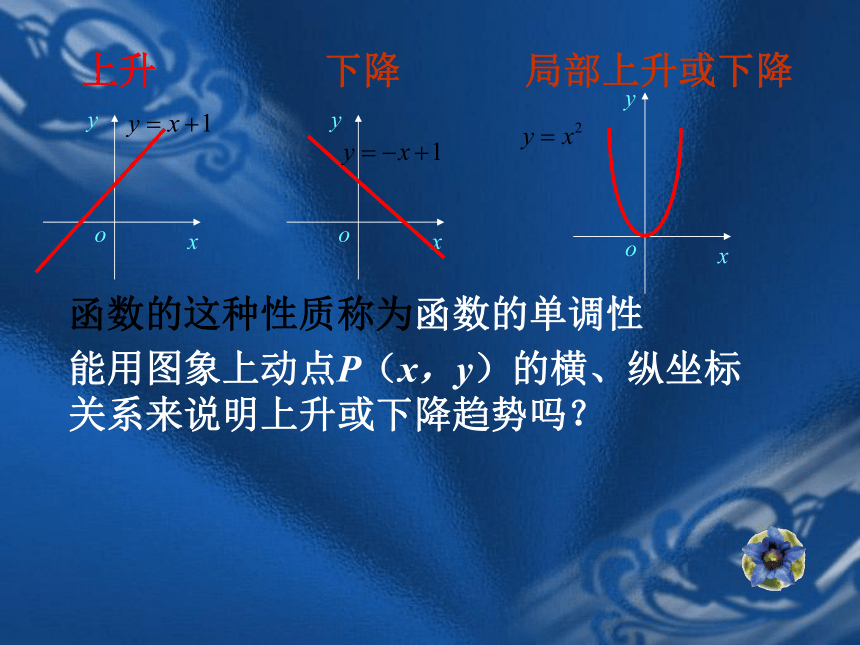
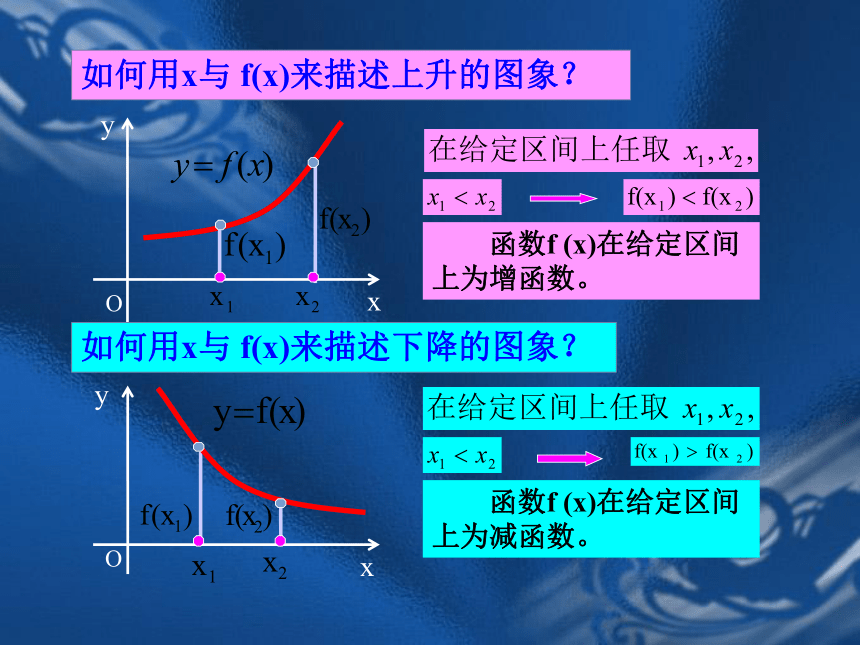
课件25张PPT。函数的单调性普通高中课程标准实验教科书(必修一)临江市8月8日一天24小时内气温随时间变化曲线图 能用图象上动点P(x,y)的横、纵坐标关系来说明上升或下降趋势吗?函数的这种性质称为函数的单调性局部上升或下降下降上升 函数f (x)在给定区间上为增函数。如何用x与 f(x)来描述上升的图象?如何用x与 f(x)来描述下降的图象? 函数f (x)在给定区间上为减函数。注意:判断:定义在R上的函数 f (x)满足 f (2)> f(1),则函数 f (x)在R上是增函数; x 1, x 2 取值的任意性OxyOxyOxyOxyOxyOxyOxyOxyOxy对于某种函数我们不能笼统地说:
函数值y随着x的增大而增大,或函数值y随着x的增大而减小。这说明函数的这一增减特征是函数的 性质。 “局部”还是“整体” ?局部当x1<x2时,都有f(x1)< f(x2), 那么就说f(x) .在这个区间上是增函数.当x1<x2时,都有f(x1)> f(x2), 那么就说f(x) .在这个区间上是减函数.增函数与减函数定义如果对于属于定义域内的某个区间上的任意两个自变量的值x1 、x2,单调区间:如果函数y=f(x)在某个区间上是单调增函数(或单调减函数),则称f(x)在这一区间上具有单调性,这一区间称为单调增(减)区间。例:下图是定义在[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一单调区间上, y=f(x)是增函数还是减函数.解:y=f(x)的单调区间有[-5,-2),[-2,1)[1,3),[3,5].其中y=f(x)在[-5,-2), [1,3)上是减函数,在[-2,1), [3,5)上是增函数.作图是发现函数单调性的方法之一. 单调区间的书写:
函数在其定义域内某一点处的函数值是确定的,讨论函数在某点处的单调性无意义。若函数在区间端点处有定义,则写成闭区间,当然写成开区间也可以,若函数在区间端点处无定于,则必须写成开区间。例1.画出下列函数图像,并写出单调区间:_____________ ,讨论1:根据函数单调性的定义, ?单调递增区间:单调递减区间:证明:(取值)(定符号)(结论)(作差)(变形)1. 值取, x1,x2∈D,且x12. 作差, f(x1)-f(x2)
3. 变形, 通常是因式分解和配方
4.定号, 即判断差f(x1)-f(x2)的正负
5.定论, 同增异减 判断或证明函数f(x)在给定的区间上的单调性的步骤:小结 取 值 → 作 差 → 变 形 → 定 号 → 下结论 1、增函数、减函数的定义 2、单调性、单调区间的概义3、单调性的证明作业:
函数值y随着x的增大而增大,或函数值y随着x的增大而减小。这说明函数的这一增减特征是函数的 性质。 “局部”还是“整体” ?局部当x1<x2时,都有f(x1)< f(x2), 那么就说f(x) .在这个区间上是增函数.当x1<x2时,都有f(x1)> f(x2), 那么就说f(x) .在这个区间上是减函数.增函数与减函数定义如果对于属于定义域内的某个区间上的任意两个自变量的值x1 、x2,单调区间:如果函数y=f(x)在某个区间上是单调增函数(或单调减函数),则称f(x)在这一区间上具有单调性,这一区间称为单调增(减)区间。例:下图是定义在[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一单调区间上, y=f(x)是增函数还是减函数.解:y=f(x)的单调区间有[-5,-2),[-2,1)[1,3),[3,5].其中y=f(x)在[-5,-2), [1,3)上是减函数,在[-2,1), [3,5)上是增函数.作图是发现函数单调性的方法之一. 单调区间的书写:
函数在其定义域内某一点处的函数值是确定的,讨论函数在某点处的单调性无意义。若函数在区间端点处有定义,则写成闭区间,当然写成开区间也可以,若函数在区间端点处无定于,则必须写成开区间。例1.画出下列函数图像,并写出单调区间:_____________ ,讨论1:根据函数单调性的定义, ?单调递增区间:单调递减区间:证明:(取值)(定符号)(结论)(作差)(变形)1. 值取, x1,x2∈D,且x1
3. 变形, 通常是因式分解和配方
4.定号, 即判断差f(x1)-f(x2)的正负
5.定论, 同增异减 判断或证明函数f(x)在给定的区间上的单调性的步骤:小结 取 值 → 作 差 → 变 形 → 定 号 → 下结论 1、增函数、减函数的定义 2、单调性、单调区间的概义3、单调性的证明作业:
