1.2.2 函数的表示法35张PPT
文档属性
| 名称 | 1.2.2 函数的表示法35张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 124.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-19 00:00:00 | ||
图片预览










文档简介
课件35张PPT。1.2.2(二)表示法函数的(1)什么叫函数?判断一个对应是否为函数有几个条件?
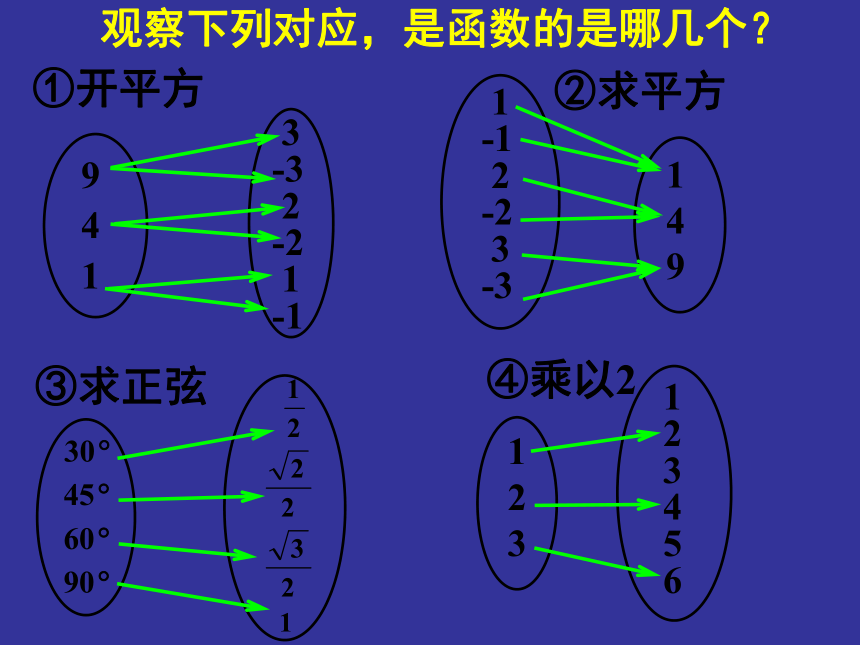
(2)函数有几种表示方法?复习①开平方③求正弦 ④乘以2 1
-1
2
-2
3
-31
4
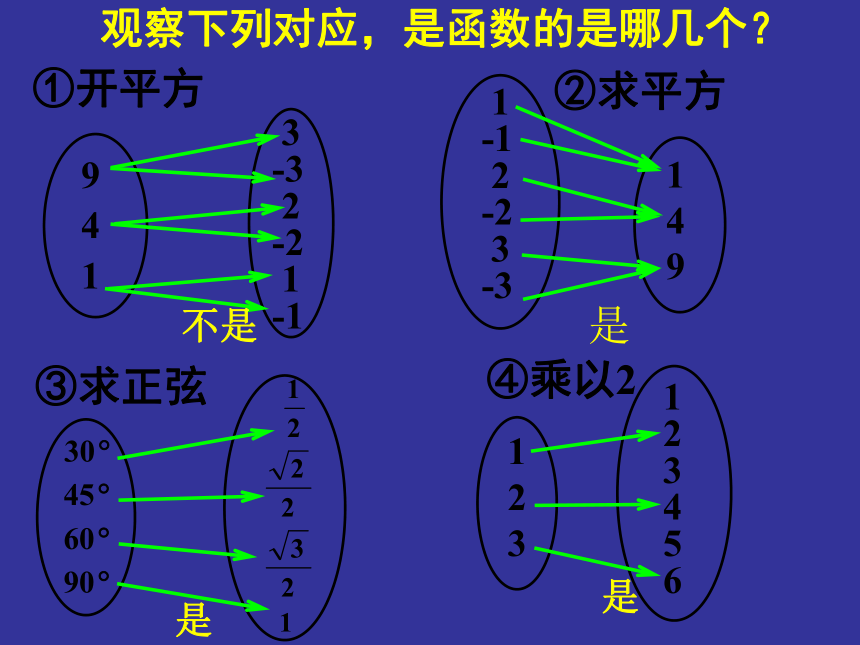
9②求平方 观察下列对应,是函数的是哪几个?①开平方③求正弦 ④乘以2 1
-1
2
-2
3
-31
4
9②求平方 观察下列对应,是函数的是哪几个?是是是不是我们已经知道,函数是建立在两个非空数集间的一种对应,若将其中的条件“非空数集”弱化为“任意两个非空集合”,按照某种法则可以建立起更为普通的元素之间的对应关系,这种对应叫映射,今天我们将研究这种特殊的对应-----映射提出问题(1)了解映射的概念及表示方法;能判断对应是否为映射。
(2)了解原象与象的概念。
(3)结合简单的对应图表,理解一一映射的概念学习目标一:映射 一般地,设A、B是两个非空集合,如果,按照某种对应关系f,对于集合A中的任
一个元素x,在集合B中都有唯一的元素y
和它对应,那么这样的对应f:A→B叫做集合A到集合B的一个映射.
映射的定义: 一般地,设A、B是两个非空集合,如果,按照某种对应关系f,对于集合A中的任
一个元素x,在集合B中都有唯一的元素y
和它对应,那么这样的对应f:A→B叫做集合A到集合B的一个映射.
思考:你能说出函数与映射的异同吗?映射的定义:函数是一个特殊的映射;映射是特殊的对应,函数映射都是对应。
2)函数中A,B都是非空数集,而对于映射,A和B不一定是数集,但一定是非空集合.理 解:一种对应是映射,必须满足什么条件?思考:一种对应是映射,必须满足条件: ①A,B都是非空数集。
② A中任何一个元素在B中都有元素与之
对应(至于B中元素是否在A中有元素对应
不必考虑,即B中可有“多余”元素). ③B中所对应的元素是唯一的 (即“一对
多”不是映射,而“多对一”可构成映
射).理 解:(例1)下列对应不是映射的是( )a
b
ce
f
g①②③(例1)下列对应不是映射的是( ② )a
b
ce
f
g①②③例2. 下列各组映射是否为同一映射?a
b
ce
f
ga
b
ce
f
g例2. 下列各组映射是否为同一映射?a
b
ce
f
ga
b
ce
f
g不是例3.(2)(4)(5)例3.(1)集合A={x|x是三角形},
集合B={x|x是圆},
对应关系f:每一个三角形都对应它的内
切圆;
(2)集合A={x|x是新华中学的班级},
集合B={x|x是新华中学的学生},
对应关系f:每一个班级都对应班里的
学生.例4. 以下给出的对应是不是从集合A到B的
映射?(1)集合A={x|x是三角形},
集合B={x|x是圆},
对应关系f:每一个三角形都对应它的内
切圆;是
(2)集合A={x|x是新华中学的班级},
集合B={x|x是新华中学的学生},
对应关系f:每一个班级都对应班里的
学生. 不是例4. 以下给出的对应是不是从集合A到B的
映射?练习:二:象与原象象与原象的定义: 给定一个集合A到B的映射,且a∈A,b∈B,若a与b对应,则把元
素b叫做a在B中的象,而a叫做b的原
象.fABab 如图(3)中,
此时象集C=B,但在(4)中,.③求正弦 ④乘以2 例5. 已知A=B=R,x∈A, y∈B,
f:x→y=ax+b,若1,8的原象相
应的是3和10,求5在f 下的象.例5. 已知A=B=R,x∈A, y∈B,
f:x→y=ax+b,若1,8的原象相
应的是3和10,求5在f 下的象.分析:分清象与原象,x的值是原象
Y的值是象;3,10是原象;1,8是象;
求出a,b,再得到结论。.例5. 已知A=B=R,x∈A, y∈B,
f:x→y=ax+b,若1,8的原象相
应的是3和10,求5在f 下的象.答案:3三:一一映射 若f是从集合A到B的映射,如果对
集合A中的不同元素在集合B中都有不
同的象,并且B中每一个元素在A中都
有原象,这样的映射叫做从集合A到集
合B的一一映射.一一映射的定义:观察下列对应并思考: 哪一个是一一映射?a
b
ce
f
g观察下列对应并思考: 哪一个是一一映射?a
b
ce
f
g一一映射不是映射映射课堂小结
(1) 理解映射的含义,能够判断一个对应是否为映射;
(2) 理解象与原象的含义,对于一个映射由原象能够求出象;由象能求出原象(3) 理解一一映射的含义,并能判断一个映射是否为一一映射。课堂小结2.课时作业8:1.教材作业P27---6, 8;3.预习下节内容.课后作业思考题. 已知A={1,2,3},
B={0,1},
写出A到B的所有映射.
(2)函数有几种表示方法?复习①开平方③求正弦 ④乘以2 1
-1
2
-2
3
-31
4
9②求平方 观察下列对应,是函数的是哪几个?①开平方③求正弦 ④乘以2 1
-1
2
-2
3
-31
4
9②求平方 观察下列对应,是函数的是哪几个?是是是不是我们已经知道,函数是建立在两个非空数集间的一种对应,若将其中的条件“非空数集”弱化为“任意两个非空集合”,按照某种法则可以建立起更为普通的元素之间的对应关系,这种对应叫映射,今天我们将研究这种特殊的对应-----映射提出问题(1)了解映射的概念及表示方法;能判断对应是否为映射。
(2)了解原象与象的概念。
(3)结合简单的对应图表,理解一一映射的概念学习目标一:映射 一般地,设A、B是两个非空集合,如果,按照某种对应关系f,对于集合A中的任
一个元素x,在集合B中都有唯一的元素y
和它对应,那么这样的对应f:A→B叫做集合A到集合B的一个映射.
映射的定义: 一般地,设A、B是两个非空集合,如果,按照某种对应关系f,对于集合A中的任
一个元素x,在集合B中都有唯一的元素y
和它对应,那么这样的对应f:A→B叫做集合A到集合B的一个映射.
思考:你能说出函数与映射的异同吗?映射的定义:函数是一个特殊的映射;映射是特殊的对应,函数映射都是对应。
2)函数中A,B都是非空数集,而对于映射,A和B不一定是数集,但一定是非空集合.理 解:一种对应是映射,必须满足什么条件?思考:一种对应是映射,必须满足条件: ①A,B都是非空数集。
② A中任何一个元素在B中都有元素与之
对应(至于B中元素是否在A中有元素对应
不必考虑,即B中可有“多余”元素). ③B中所对应的元素是唯一的 (即“一对
多”不是映射,而“多对一”可构成映
射).理 解:(例1)下列对应不是映射的是( )a
b
ce
f
g①②③(例1)下列对应不是映射的是( ② )a
b
ce
f
g①②③例2. 下列各组映射是否为同一映射?a
b
ce
f
ga
b
ce
f
g例2. 下列各组映射是否为同一映射?a
b
ce
f
ga
b
ce
f
g不是例3.(2)(4)(5)例3.(1)集合A={x|x是三角形},
集合B={x|x是圆},
对应关系f:每一个三角形都对应它的内
切圆;
(2)集合A={x|x是新华中学的班级},
集合B={x|x是新华中学的学生},
对应关系f:每一个班级都对应班里的
学生.例4. 以下给出的对应是不是从集合A到B的
映射?(1)集合A={x|x是三角形},
集合B={x|x是圆},
对应关系f:每一个三角形都对应它的内
切圆;是
(2)集合A={x|x是新华中学的班级},
集合B={x|x是新华中学的学生},
对应关系f:每一个班级都对应班里的
学生. 不是例4. 以下给出的对应是不是从集合A到B的
映射?练习:二:象与原象象与原象的定义: 给定一个集合A到B的映射,且a∈A,b∈B,若a与b对应,则把元
素b叫做a在B中的象,而a叫做b的原
象.fABab 如图(3)中,
此时象集C=B,但在(4)中,.③求正弦 ④乘以2 例5. 已知A=B=R,x∈A, y∈B,
f:x→y=ax+b,若1,8的原象相
应的是3和10,求5在f 下的象.例5. 已知A=B=R,x∈A, y∈B,
f:x→y=ax+b,若1,8的原象相
应的是3和10,求5在f 下的象.分析:分清象与原象,x的值是原象
Y的值是象;3,10是原象;1,8是象;
求出a,b,再得到结论。.例5. 已知A=B=R,x∈A, y∈B,
f:x→y=ax+b,若1,8的原象相
应的是3和10,求5在f 下的象.答案:3三:一一映射 若f是从集合A到B的映射,如果对
集合A中的不同元素在集合B中都有不
同的象,并且B中每一个元素在A中都
有原象,这样的映射叫做从集合A到集
合B的一一映射.一一映射的定义:观察下列对应并思考: 哪一个是一一映射?a
b
ce
f
g观察下列对应并思考: 哪一个是一一映射?a
b
ce
f
g一一映射不是映射映射课堂小结
(1) 理解映射的含义,能够判断一个对应是否为映射;
(2) 理解象与原象的含义,对于一个映射由原象能够求出象;由象能求出原象(3) 理解一一映射的含义,并能判断一个映射是否为一一映射。课堂小结2.课时作业8:1.教材作业P27---6, 8;3.预习下节内容.课后作业思考题. 已知A={1,2,3},
B={0,1},
写出A到B的所有映射.
