函数的单调性课件61张PPT
图片预览


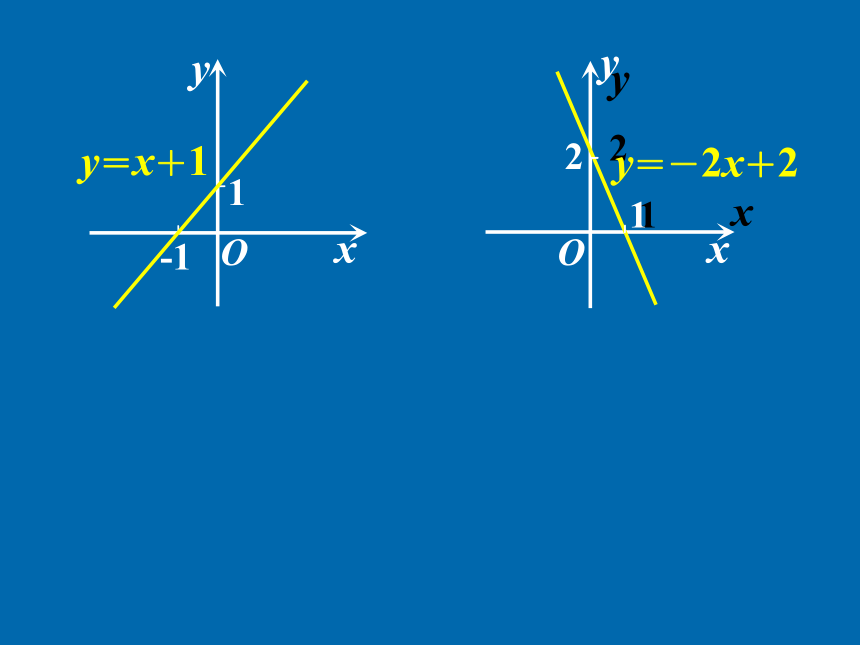
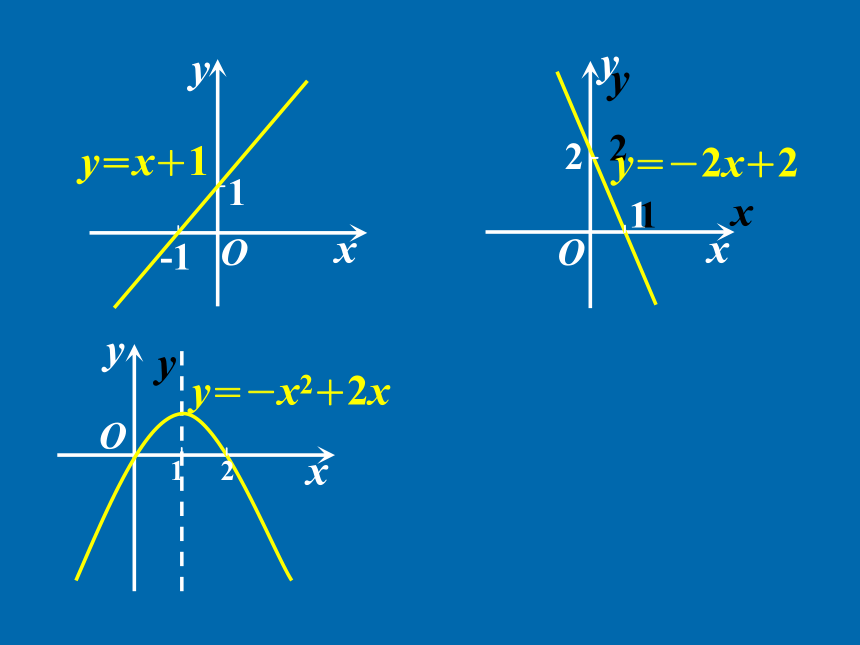
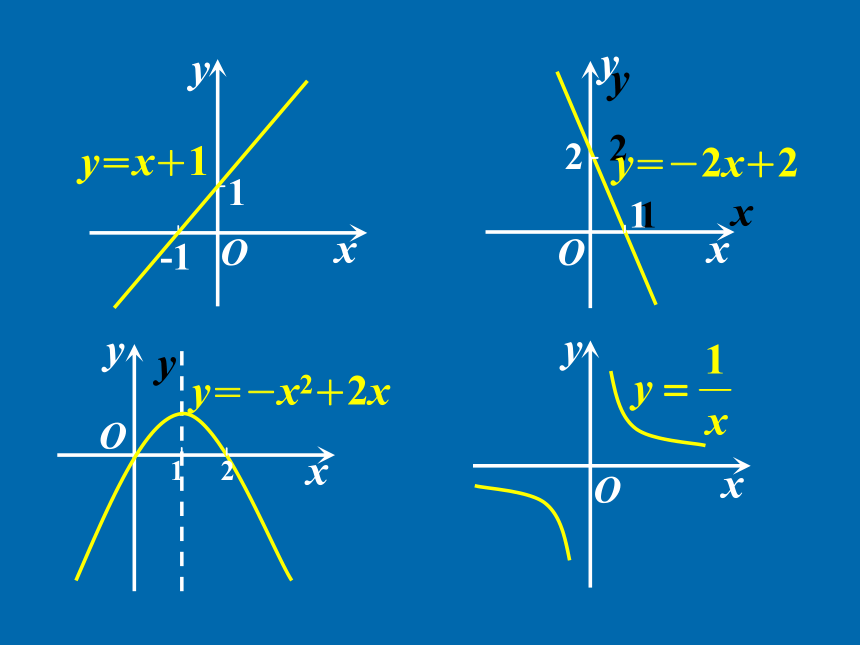

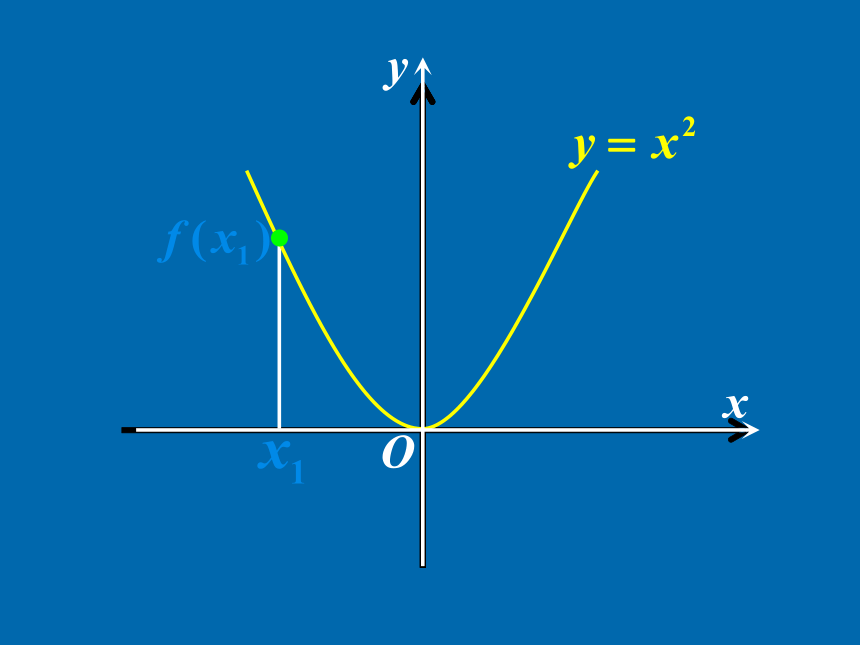
文档简介
课件61张PPT。1.3 函数的基本性质
——单调性y=x+1 1-1Oyxxy21xy21y=x+1 1-1OOyxy=-2x+2 xy21xy21y=x+1 1-1y21OOOyyxxy=-2x+2 y=-x2+2x xy21xy21yxOy=x+1 1-1y21OOOyyxxy=-2x+2 y=-x2+2x xyOxyO0xyO如何用x与f(x)来描述上升的图象?Oxy如何用x与f(x)来描述上升的图象?Oxy如何用x与f(x)来描述上升的图象?Oxy如何用x与f(x)来描述上升的图象?Oxyx1<x2如何用x与f(x)来描述上升的图象?Oxyy=f(x)x1<x2如何用x与f(x)来描述上升的图象?Oxyy=f(x)x1<x2如何用x与f(x)来描述上升的图象?Oxyy=f(x)x1<x2如何用x与f(x)来描述上升的图象?Oxyy=f(x)x1<x2? f(x1)<f(x2)如何用x与f(x)来描述上升的图象?Oxyy=f(x)x1<x2? f(x1)<f(x2)如何用x与f(x)来描述上升的图象?Oxyy=f(x)如何用x与f(x)来描述上升的图象?Oxyy=f(x)在给定区间上任取x1, x2x1<x2 ? f(x1)<f(x2)如何用x与f(x)来描述上升的图象?Oxyy=f(x)在给定区间上任取x1, x2x1<x2 ? f(x1)<f(x2)如何用x与f(x)来描述上升的图象?Oxyy=f(x)在给定区间上任取x1, x2 函数f (x)在给定
区间上为增函数.x1<x2 ? f(x1)<f(x2)如何用x与f(x)来描述上升的图象?Oxyy=f(x)在给定区间上任取x1, x2如何用x与f(x)来描述下降的图象?x2x1Oxyy=f(x)f(x1)f(x2) 函数f (x)在给定
区间上为增函数.x1<x2 ? f(x1)<f(x2)如何用x与f(x)来描述上升的图象?Oxyy=f(x)在给定区间上任取x1, x2如何用x与f(x)来描述下降的图象?x2x1Oxyy=f(x)f(x1)f(x2) 函数f (x)在给定
区间上为增函数.在给定区间上任取x1, x2x1<x2 ? f(x1)<f(x2)如何用x与f(x)来描述上升的图象?Oxyy=f(x)在给定区间上任取x1, x2如何用x与f(x)来描述下降的图象?x2x1Oxyy=f(x)f(x1)f(x2) 函数f (x)在给定
区间上为增函数.x1<x2 ? f(x1)>f(x2)在给定区间上任取x1, x2x1<x2 ? f(x1)<f(x2)如何用x与f(x)来描述上升的图象?Oxyy=f(x)在给定区间上任取x1, x2如何用x与f(x)来描述下降的图象?x2x1Oxyy=f(x)f(x1)f(x2) 函数f (x)在给定
区间上为增函数. 函数f (x)在给定
区间上为减函数.x1<x2 ? f(x1)>f(x2)在给定区间上任取x1, x2增函数、减函数的概念:增函数、减函数的概念:一般地,设函数f(x)的定义域为I.1.如果对于定义域I内的某个区间上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)<f(x2),那么就说f(x)在这个区间上是
增函数.
增函数、减函数的概念:一般地,设函数f(x)的定义域为I.1.如果对于定义域I内的某个区间上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)<f(x2),那么就说f(x)在这个区间上是
增函数.
2.如果对于定义域I内的某个区间上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)>f(x2),那么就说f(x)在这个区间上是
减函数.增函数、减函数的概念:一般地,设函数f(x)的定义域为I.1.如果对于定义域I内的某个区间上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)<f(x2),那么就说f(x)在这个区间上是
增函数.
2.如果对于定义域I内的某个区间上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)>f(x2),那么就说f(x)在这个区间上是
减函数.一般地,设函数f(x)的定义域为I.增函数、减函数的概念:1.如果对于定义域I内的某个区间上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)<f(x2),那么就说f(x)在这个区间上是
增函数.
2.如果对于定义域I内的某个区间上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)>f(x2),那么就说f(x)在这个区间上是
减函数.一般地,设函数f(x)的定义域为I.增函数、减函数的概念:1.如果对于定义域I内的某个区间上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)<f(x2),那么就说f(x)在这个区间上是
增函数.
2.如果对于定义域I内的某个区间上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)>f(x2),那么就说f(x)在这个区间上是
减函数.增函数、减函数的概念:一般地,设函数f(x)的定义域为I.1.如果对于定义域I内的某个区间上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)<f(x2),那么就说f(x)在这个区间上是
增函数.
2.如果对于定义域I内的某个区间上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)>f(x2),那么就说f(x)在这个区间上是
减函数.增函数、减函数的概念:一般地,设函数f(x)的定义域为I.1.如果对于定义域I内的某个区间上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)<f(x2),那么就说f(x)在这个区间上是
增函数.
2.如果对于定义域I内的某个区间上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)>f(x2),那么就说f(x)在这个区间上是
减函数.增函数、减函数的概念:一般地,设函数f(x)的定义域为I.1.如果对于定义域I内的某个区间上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)<f(x2),那么就说f(x)在这个区间上是
增函数.
2.如果对于定义域I内的某个区间上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)>f(x2),那么就说f(x)在这个区间上是
减函数.一般地,设函数f(x)的定义域为I.增函数、减函数的概念:函数单调性的概念:函数单调性的概念:函数单调性的概念:-2321-1y-3-44Ox2-231-3-15-5例1 右图是定义在
闭区间[-5, 5]上
的函数y=f(x)的图
象,根据图象说出
y=f(x)的单调区间,
以及在每一单调区
间上, y=f(x)是增函数还是减函数.例1 右图是定义在
闭区间[-5, 5]上
的函数y=f(x)的图
象,根据图象说出
y=f(x)的单调区间,
以及在每一单调区
间上, y=f(x)是增函数还是减函数.-2321-1y-3-44Ox2-231-3-15-5 函数y=f(x)的单调区间有[-5,-2),
[-2, 1),[1, 3),[3, 5],解:-2321-1y-3-44Ox2-231-3-15-5 函数y=f(x)的单调区间有[-5,-2),
[-2, 1),[1, 3),[3, 5],其中y=f(x)在[-5,-2),[1, 3)上是减函数,
在区间[-2, 1),[3, 5]上是增函数.解:例1 右图是定义在
闭区间[-5, 5]上
的函数y=f(x)的图
象,根据图象说出
y=f(x)的单调区间,
以及在每一单调区
间上, y=f(x)是增函数还是减函数.-2321-1y-3-44Ox2-231-3-15-5 函数y=f(x)的单调区间有[-5,-2),
[-2, 1),[1, 3),[3, 5],其中y=f(x)在[-5,-2),[1, 3)上是减函数,
在区间[-2, 1),[3, 5]上是增函数.图象法解:例1 右图是定义在
闭区间[-5, 5]上
的函数y=f(x)的图
象,根据图象说出
y=f(x)的单调区间,
以及在每一单调区
间上, y=f(x)是增函数还是减函数.例2 证明:函数f(x)=3x+2在R上是增函数. 判定函数在某个区间上的单调性的
方法步骤:3. 判断上述差的符号;4. 下结论1. 设x1, x2∈给定的区间,且x1<x2;2. 计算f(x1)-f(x2) 至最简;(若差<0,则为增函数;
若差>0,则为减函数).定义法例2 证明:函数f(x)=3x+2在R上是增函数.定义法变式1:函数f(x)=-3x+2在R上是增函数
还是减函数?例2 证明:函数f(x)=3x+2在R上是增函数.定义法变式2:函数f(x)=kx+b(k≠0)在R上是增
函数还是减函数?并证明.变式1:函数f(x)=-3x+2在R上是增函数
还是减函数?例2 证明:函数f(x)=3x+2在R上是增函数.例3 证明:函数f(x)= 在(0, +∞)上是
减函数.变式1:f(x)= 在(-∞, 0)上是增函数
还是减函数?例3 证明:函数f(x)= 在(0, +∞)上是
减函数.变式1:f(x)= 在(-∞, 0)上是增函数
还是减函数?变式2:讨论函数f(x)= 在定义域上的
单调性.例3 证明:函数f(x)= 在(0, +∞)上是
减函数.变式1:f(x)= 在(-∞, 0)上是增函数
还是减函数?变式2:讨论函数f(x)= 在定义域上的
单调性.结论:函数f(x)= 在其定义域上不具有
单调性.例3 证明:函数f(x)= 在(0, +∞)上是
减函数.1.两个定义:增函数、减函数. 课堂小结1.两个定义:增函数、减函数. 2.两种方法:判断函数单调性的方法
有图象法、定义法.课堂小结1.阅读教材P.27 -P.30;
2.《习案》:作业9.课后作业
——单调性y=x+1 1-1Oyxxy21xy21y=x+1 1-1OOyxy=-2x+2 xy21xy21y=x+1 1-1y21OOOyyxxy=-2x+2 y=-x2+2x xy21xy21yxOy=x+1 1-1y21OOOyyxxy=-2x+2 y=-x2+2x xyOxyO0xyO如何用x与f(x)来描述上升的图象?Oxy如何用x与f(x)来描述上升的图象?Oxy如何用x与f(x)来描述上升的图象?Oxy如何用x与f(x)来描述上升的图象?Oxyx1<x2如何用x与f(x)来描述上升的图象?Oxyy=f(x)x1<x2如何用x与f(x)来描述上升的图象?Oxyy=f(x)x1<x2如何用x与f(x)来描述上升的图象?Oxyy=f(x)x1<x2如何用x与f(x)来描述上升的图象?Oxyy=f(x)x1<x2? f(x1)<f(x2)如何用x与f(x)来描述上升的图象?Oxyy=f(x)x1<x2? f(x1)<f(x2)如何用x与f(x)来描述上升的图象?Oxyy=f(x)如何用x与f(x)来描述上升的图象?Oxyy=f(x)在给定区间上任取x1, x2x1<x2 ? f(x1)<f(x2)如何用x与f(x)来描述上升的图象?Oxyy=f(x)在给定区间上任取x1, x2x1<x2 ? f(x1)<f(x2)如何用x与f(x)来描述上升的图象?Oxyy=f(x)在给定区间上任取x1, x2 函数f (x)在给定
区间上为增函数.x1<x2 ? f(x1)<f(x2)如何用x与f(x)来描述上升的图象?Oxyy=f(x)在给定区间上任取x1, x2如何用x与f(x)来描述下降的图象?x2x1Oxyy=f(x)f(x1)f(x2) 函数f (x)在给定
区间上为增函数.x1<x2 ? f(x1)<f(x2)如何用x与f(x)来描述上升的图象?Oxyy=f(x)在给定区间上任取x1, x2如何用x与f(x)来描述下降的图象?x2x1Oxyy=f(x)f(x1)f(x2) 函数f (x)在给定
区间上为增函数.在给定区间上任取x1, x2x1<x2 ? f(x1)<f(x2)如何用x与f(x)来描述上升的图象?Oxyy=f(x)在给定区间上任取x1, x2如何用x与f(x)来描述下降的图象?x2x1Oxyy=f(x)f(x1)f(x2) 函数f (x)在给定
区间上为增函数.x1<x2 ? f(x1)>f(x2)在给定区间上任取x1, x2x1<x2 ? f(x1)<f(x2)如何用x与f(x)来描述上升的图象?Oxyy=f(x)在给定区间上任取x1, x2如何用x与f(x)来描述下降的图象?x2x1Oxyy=f(x)f(x1)f(x2) 函数f (x)在给定
区间上为增函数. 函数f (x)在给定
区间上为减函数.x1<x2 ? f(x1)>f(x2)在给定区间上任取x1, x2增函数、减函数的概念:增函数、减函数的概念:一般地,设函数f(x)的定义域为I.1.如果对于定义域I内的某个区间上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)<f(x2),那么就说f(x)在这个区间上是
增函数.
增函数、减函数的概念:一般地,设函数f(x)的定义域为I.1.如果对于定义域I内的某个区间上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)<f(x2),那么就说f(x)在这个区间上是
增函数.
2.如果对于定义域I内的某个区间上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)>f(x2),那么就说f(x)在这个区间上是
减函数.增函数、减函数的概念:一般地,设函数f(x)的定义域为I.1.如果对于定义域I内的某个区间上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)<f(x2),那么就说f(x)在这个区间上是
增函数.
2.如果对于定义域I内的某个区间上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)>f(x2),那么就说f(x)在这个区间上是
减函数.一般地,设函数f(x)的定义域为I.增函数、减函数的概念:1.如果对于定义域I内的某个区间上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)<f(x2),那么就说f(x)在这个区间上是
增函数.
2.如果对于定义域I内的某个区间上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)>f(x2),那么就说f(x)在这个区间上是
减函数.一般地,设函数f(x)的定义域为I.增函数、减函数的概念:1.如果对于定义域I内的某个区间上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)<f(x2),那么就说f(x)在这个区间上是
增函数.
2.如果对于定义域I内的某个区间上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)>f(x2),那么就说f(x)在这个区间上是
减函数.增函数、减函数的概念:一般地,设函数f(x)的定义域为I.1.如果对于定义域I内的某个区间上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)<f(x2),那么就说f(x)在这个区间上是
增函数.
2.如果对于定义域I内的某个区间上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)>f(x2),那么就说f(x)在这个区间上是
减函数.增函数、减函数的概念:一般地,设函数f(x)的定义域为I.1.如果对于定义域I内的某个区间上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)<f(x2),那么就说f(x)在这个区间上是
增函数.
2.如果对于定义域I内的某个区间上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)>f(x2),那么就说f(x)在这个区间上是
减函数.增函数、减函数的概念:一般地,设函数f(x)的定义域为I.1.如果对于定义域I内的某个区间上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)<f(x2),那么就说f(x)在这个区间上是
增函数.
2.如果对于定义域I内的某个区间上的任意
两个自变量的值x1, x2,当x1<x2时,都有
f(x1)>f(x2),那么就说f(x)在这个区间上是
减函数.一般地,设函数f(x)的定义域为I.增函数、减函数的概念:函数单调性的概念:函数单调性的概念:函数单调性的概念:-2321-1y-3-44Ox2-231-3-15-5例1 右图是定义在
闭区间[-5, 5]上
的函数y=f(x)的图
象,根据图象说出
y=f(x)的单调区间,
以及在每一单调区
间上, y=f(x)是增函数还是减函数.例1 右图是定义在
闭区间[-5, 5]上
的函数y=f(x)的图
象,根据图象说出
y=f(x)的单调区间,
以及在每一单调区
间上, y=f(x)是增函数还是减函数.-2321-1y-3-44Ox2-231-3-15-5 函数y=f(x)的单调区间有[-5,-2),
[-2, 1),[1, 3),[3, 5],解:-2321-1y-3-44Ox2-231-3-15-5 函数y=f(x)的单调区间有[-5,-2),
[-2, 1),[1, 3),[3, 5],其中y=f(x)在[-5,-2),[1, 3)上是减函数,
在区间[-2, 1),[3, 5]上是增函数.解:例1 右图是定义在
闭区间[-5, 5]上
的函数y=f(x)的图
象,根据图象说出
y=f(x)的单调区间,
以及在每一单调区
间上, y=f(x)是增函数还是减函数.-2321-1y-3-44Ox2-231-3-15-5 函数y=f(x)的单调区间有[-5,-2),
[-2, 1),[1, 3),[3, 5],其中y=f(x)在[-5,-2),[1, 3)上是减函数,
在区间[-2, 1),[3, 5]上是增函数.图象法解:例1 右图是定义在
闭区间[-5, 5]上
的函数y=f(x)的图
象,根据图象说出
y=f(x)的单调区间,
以及在每一单调区
间上, y=f(x)是增函数还是减函数.例2 证明:函数f(x)=3x+2在R上是增函数. 判定函数在某个区间上的单调性的
方法步骤:3. 判断上述差的符号;4. 下结论1. 设x1, x2∈给定的区间,且x1<x2;2. 计算f(x1)-f(x2) 至最简;(若差<0,则为增函数;
若差>0,则为减函数).定义法例2 证明:函数f(x)=3x+2在R上是增函数.定义法变式1:函数f(x)=-3x+2在R上是增函数
还是减函数?例2 证明:函数f(x)=3x+2在R上是增函数.定义法变式2:函数f(x)=kx+b(k≠0)在R上是增
函数还是减函数?并证明.变式1:函数f(x)=-3x+2在R上是增函数
还是减函数?例2 证明:函数f(x)=3x+2在R上是增函数.例3 证明:函数f(x)= 在(0, +∞)上是
减函数.变式1:f(x)= 在(-∞, 0)上是增函数
还是减函数?例3 证明:函数f(x)= 在(0, +∞)上是
减函数.变式1:f(x)= 在(-∞, 0)上是增函数
还是减函数?变式2:讨论函数f(x)= 在定义域上的
单调性.例3 证明:函数f(x)= 在(0, +∞)上是
减函数.变式1:f(x)= 在(-∞, 0)上是增函数
还是减函数?变式2:讨论函数f(x)= 在定义域上的
单调性.结论:函数f(x)= 在其定义域上不具有
单调性.例3 证明:函数f(x)= 在(0, +∞)上是
减函数.1.两个定义:增函数、减函数. 课堂小结1.两个定义:增函数、减函数. 2.两种方法:判断函数单调性的方法
有图象法、定义法.课堂小结1.阅读教材P.27 -P.30;
2.《习案》:作业9.课后作业
