函数的单调性与最值47张PPT

课件47张PPT。函数的单调性与最值
【教材知识精梳理】
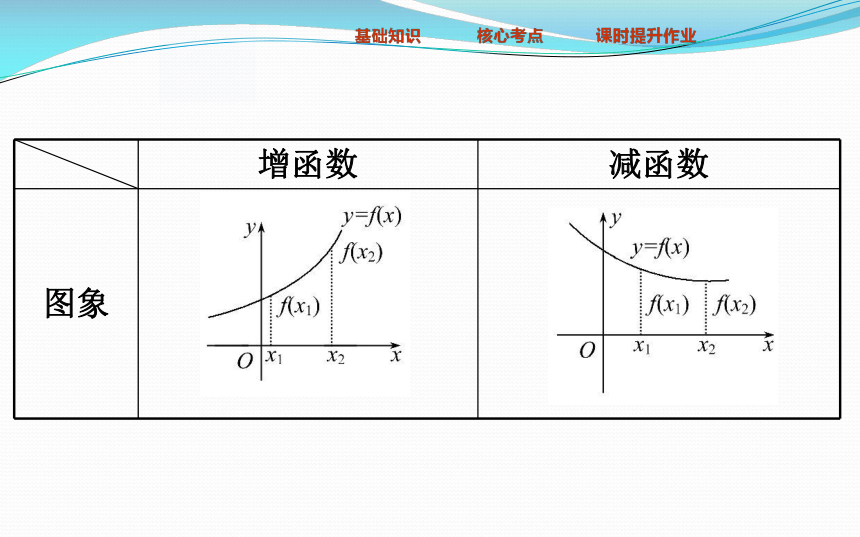
1.增函数、减函数任意f(x1)f(x2)2.单调性、单调区间的定义
若函数y=f(x)在区间D上是_______或_______,则称
函数y=f(x)在这一区间具有(严格的)单调性,区间D
叫做函数y=f(x)的单调区间.增函数减函数3.函数的最值f(x)≤Mf(x)≥M【教材拓展微思考】
1.定义在R上的函数y=f(x)中有f(-2)提示:不一定,因为-2和3只是定义域R上的两个特殊值,不能说明对任意的x1提示:当函数是增函数时,x1-x2与f(x1)-f(x2)同号;当函数是减函数时,x1-x2与f(x1)-f(x2)异号.3.在最大值、最小值的定义中,条件(2)能否去掉?为什么?
提示:不能,因为去掉后不能保证M是一个函数值,即存在一个x0∈I,使M=f(x0),最大值、最小值必须是函数值中的最大值、最小值.诊 断 自 测1.判断正误(在括号内打“√”或“×”)　 解析　(2)此单调区间不能用并集符号连接，取x1＝－1，x2＝1，则f(－1)＜f(1)，故应说成单调递减区间为(－∞，0)和(0，＋∞).
(3)应对任意的x1＜x2，f(x1)＜f(x2)成立才可以.
(4)若f(x)＝x，f(x)在[1，＋∞)上为增函数，但y＝f(x)的单调递增区间可以是R.
答案　(1)√　(2)×　(3)×　(4)×考向一　确定函数的单调性(区间)　　　
【典例】(1)(2016·北京高考)下列函数中,在区间
(-1,1)上为减函数的是　(　　)
A.y= B.y=cosx
C.y=ln(x+1) D.y=2-x(2)判断并证明函数f(x)=ax2+
(其中1(2)利用定义法进行判断.【规范解答】(1)选D.选项A定义域为{x|x≠1},
不符合题意;
选项B在(-1,1)上先增后减;
选项C在(-1,1)上单调递增;
只有选项D符合题意.(2)设1≤x1f(x2)-f(x1)=
=(x2-x1)
由1≤x10,21所以2得a(x1+x2)- >0,
从而f(x2)-f(x1)>0,
即f(x2)>f(x1),
故当a∈(1,3)时,f(x)在[1,2]上单调递增.【一题多解】因为f′(x)=2ax- 而x∈[1,2],所以
-1≤ 又因为a∈(1,3),所以2<2ax<12,故2ax-
>0,即f′(x)>0,故当a∈(1,3)时,f(x)在[1,2]上单
调递增.【母题变式】
1.若本例(1)中D选项变为y=2-sinx,则结果如何?
【解析】选D.选项A,B,C解析同典例(1)解析,D选项中
y=2-sinx= 令μ=sinx,则该函数在(-1,1)上为增
函数,而y= 在R上为减函数,故y=2-sinx在(-1,1)上
为减函数.2.若本例(2)中函数变为f(x)= (a≠0),试求其
在(-1,1)上的单调性.
【解析】方法一(定义法):设-1f(x)=
f(x1)-f(x2)=
由于-10,x1-1<0,x2-1<0,
故当a>0时,f(x1)-f(x2)>0,
即f(x1)>f(x2),
函数f(x)在(-1,1)上递减;
当a<0时,f(x1)-f(x2)<0,即f(x1)函数f(x)在(-1,1)上递增.方法二(导数法):
当a>0时,f′(x)<0,函数f(x)在(-1,1)上递减;
当a<0时,f′(x)>0,函数f(x)在(-1,1)上递增.【技法点拨】
确定函数单调性(区间)的常用方法
(1)定义法:一般步骤为设元→作差→变形→判断符号→得出结论.其关键是作差变形,为了便于判断差的符号,通常将差变成因式连乘(除)或平方和的形式,再结合变量的范围、假定的两个自变量的大小关系及不等式的性质进行判断.(2)图象法:如果f(x)是以图象形式给出的,或者f(x)的图象易作出,则可由图象的直观性确定它的单调性.
(3)导数法:利用导数取值的正负确定函数的单调性.(4)复合函数单调性的判断法则:“同增异减”,即对于y=f(g(x))型的复合函数,可以把它看成由y=f(t)和t=g(x)复合而成的,若它们的单调性相同,则复合后的函数为增函数;若它们的单调性相反,则复合后的函数为减函数.提醒:1.单调区间是定义域的子集,故求单调区间应以“定义域优先”为原则.
2.单调区间只能用区间表示,不能用集合或不等式表示.
3.图象不连续的单调区间要分开写,用“和”“或” “,”连接,不能用“∪”连接.考向二　求函数的最值(值域)
【技法点拨】
求函数最值(值域)的五种常用方法
(1)单调性法:先确定函数的单调性,再由单调性求最值.(2)图象法:先作出函数的图象,再观察其最高点、最低点,求出最值.
(3)基本不等式法:先对解析式变形,使之具备“一正二定三相等”的条件后用基本不等式求出最值.(4)导数法:先求导,然后求出在给定区间上的极值,最后结合端点值,求出最值.
(5)换元法:对比较复杂的函数可通过换元转化为熟悉的函数,再用相应的方法求最值.【基础保分题组】
1.若函数f(x)=x2-2x+m在[3,+∞)上的最小值为1,则实数m的值为　(　　)
A.-3 B.-2 C.-1 D.1【解析】选B.函数f(x)=x2-2x+m=(x-1)2+m-1的图象
如图所示.由图象知在[3,+∞)上f(x)min=f(3)=32-
2×3+m=1,得m=-2.2.函数f(x)= 在区间[a,b]上的最大值是1,最小值
是 则a+b=________.【解析】由题易知f(x)在[a,b]上为减函数,
所以a+b=6.
答案:63.函数y= -x(x≥0)的最大值为________.
【解析】令t= ,则t≥0,所以y=t-t2=
当t= ,即x= 时,ymax=
答案: 【拓展提升——高考模拟预测】
4.函数f(x)= (x≥2)的最大值为________.【解析】令t=x-1(t≥1),则x=t+1,所以y=
(t≥1).所以0< ≤1,所以1<1+ ≤2.所以f(x)的
最大值为2.
答案:25.若不等式a> 在(0,+∞)上恒成立,则实数a的
取值范围为________.
【解析】令f(x)=
当且仅当x=2时,等号成立,所以由已知得a>
答案: 6.对于任意实数a,b,定义min{a,b}= 设函数f(x)=-x+3,g(x)=log2x,则函数h(x)=min{f(x),g(x)}的最大值是________.
【解析】依题意,h(x)=
当0当x>2时,h(x)=3-x是减函数,
所以h(x)在x=2时取得最大值h(2)=1.
答案:1【加固训练】1.函数f(x)= 的最大值为
________.【解析】当x≥1时,函数f(x)= 为减函数,所以f(x)
在x=1处取得最大值,为f(1)=1;当x<1时,易知函数
f(x)=-x2+2在x=0处取得最大值,为f(0)=2.
故函数f(x)的最大值为2.
答案:22.用min{a,b,c}表示a,b,c三个数中的最小值,则函数f(x)=min{4x+1,x+4,-x+8}的最大值是________.【解析】在同一坐标系中分别作出函数y=4x+1,
y=x+4,y=-x+8的图象后,取位于下方
的部分得函数f(x)=min{4x+1,x+4,
-x+8}的图象,如图所示,由图象可
知,函数f(x)在x=2时取得最大值6.
答案:6[思想方法]
1.利用定义证明或判断函数单调性的步骤：
(1)取值 ；(2)作差；(3)定号；(4)判断.
2.确定函数单调性有四种常用方法：定义法、导数法、复合函数法、图像法，也可利用单调函数的和差确定单调性.
3.求函数最值的常用求法：单调性法、图像法、换元法、利用基本不等式.闭区间上的连续函数一定存在最大值和最小值，当函数在闭区间上单调时，最值一定在端点处取到.作业：课时作业本第239页