应用数形结合思想解决数学问题

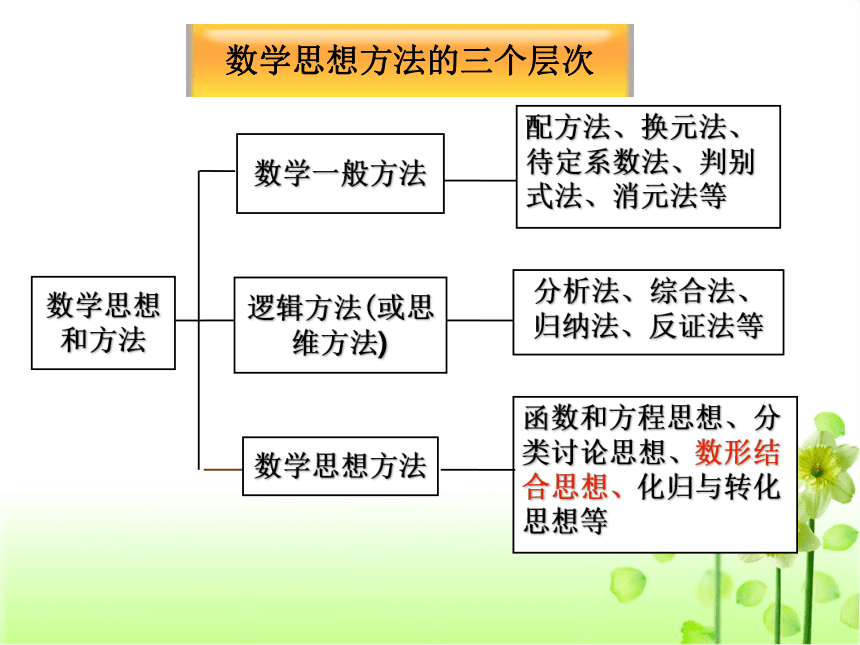
课件25张PPT。数学思想方法的三个层次数学专题 应用“数形结合”思想解决问题
　　公元5世纪祖冲之取得了圆周率计算的一个跃进 ，他也最早提出“数形结合”解题的数学思想。数形本是两依倚
焉能分作两边飞
数缺形时少直观
形缺数时难入微 把数量关系的研究转化为
图形性质的研究，或者把图形
性质的研究转化为数量关系的研究，这种 “数”与“形”相互转化的解题策略，就是数形结合的思想. 数形结合就是把抽象的数学语言与直观的图形相结合，通过“以形助数”或“以数解形”，使抽象问题具体化，复杂问题简单化，从而起到优化解题途径的目的．
数形结合的重点是研究“以形助数”．数形结合思想应用“数形结合”思想解决问题
　　解：由已知答案:(-2,1)∪（1,2）B【点评】　求参数范围、零点、交点个数等问题经常联系函数的图象，选择适当的两个(或多个)函数，利用两个函数图象的上、下位置关系转化数量关系来解决问题，往往可以避免繁琐的运算，获得简捷的解答．
例4.不等式 的解集是 .

解析 方法一(代数运算）综上：不等式的解集为x∈(2,4] 方法二 数形结合法，
令 则(x-2)2+y2=4 (y≥0)其图象是半圆，在同一直角坐标系中，分别作出 y=x的图象，
.22xy4 答案: （2，4］思考:不等式 的解集是(0,2) ［点评］本题很好地体现了数形结合的优越性，如果单纯地从数的观点来解题的话，得出m=－a与n=a也是有一定的难度的，但从形的角度出发，可以很直观地看出，这也就说明了解小题时一
定要重视这种思想的应用.mn 由图象m=－a,再由|m－n|=2a得到n=a,因为n为方程的根,所以将a的只带代入方程得a=2B评注：割补法是几何图形变换的基本方法.把不规则的图形通过割补转化为规则的图形，从而使问题得到解决.体现了转化和数形结合的思想.
三、用“数形结合” 求面积和交点解法1： 解法2：解法3（１，１）分离常数法　图解法答案：　反函数法12和3.评注：借助图像将抽象的问题具体化，通过图象直观性形象的解决问题。练习1：课堂练习：课堂小结　
在运用数形结合思想分析和解决问题时，要注意三点：
①要彻底弄清一些概念和运算的几何意义以及曲线的代数特征，对数学题目中的条件和结论，既分析其几何意义又分析其代数意义．
②要恰当设立参数，合理建立关系，由数思形，以形思数，做好数形转化．
③要正确确定参数的取值范围．谢谢大家