3.1.2 导数的概念27张PPT
文档属性
| 名称 | 3.1.2 导数的概念27张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 949.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-19 00:00:00 | ||
图片预览





文档简介
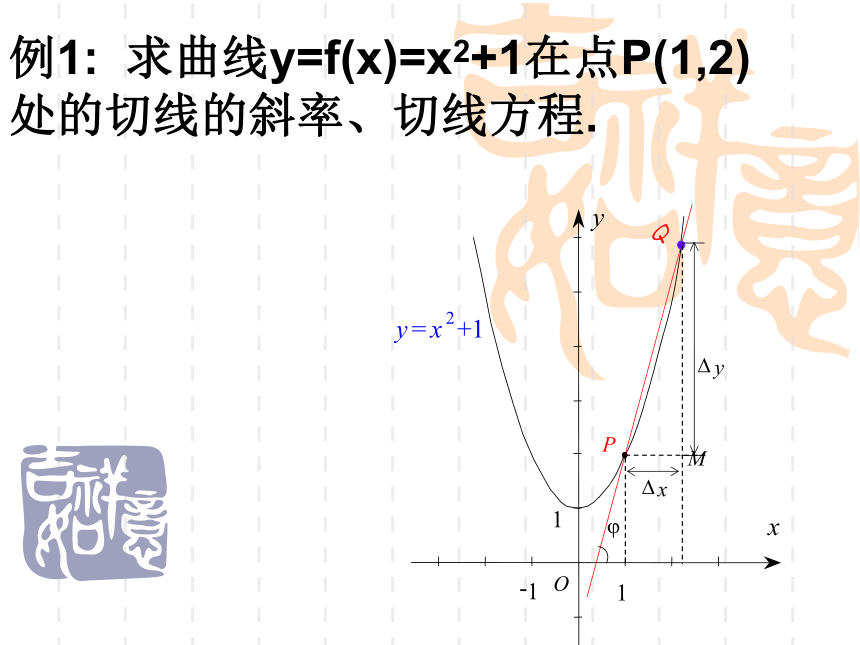
课件27张PPT。导数的概念基本初等函数的导数公式:1. 利用导数求瞬时速度例1:物体作自由落体运动,运动方程为: 其中位 移单位是m,时间单位是s,g=10m/s2.则 物体在t=2 s时的瞬时速度为 . 例1: 求曲线y=f(x)=x2+1在点P(1,2)处的切线的斜率、切线方程.练习:如图,已知曲线 , 求:
(1)点P处的切线的斜率;
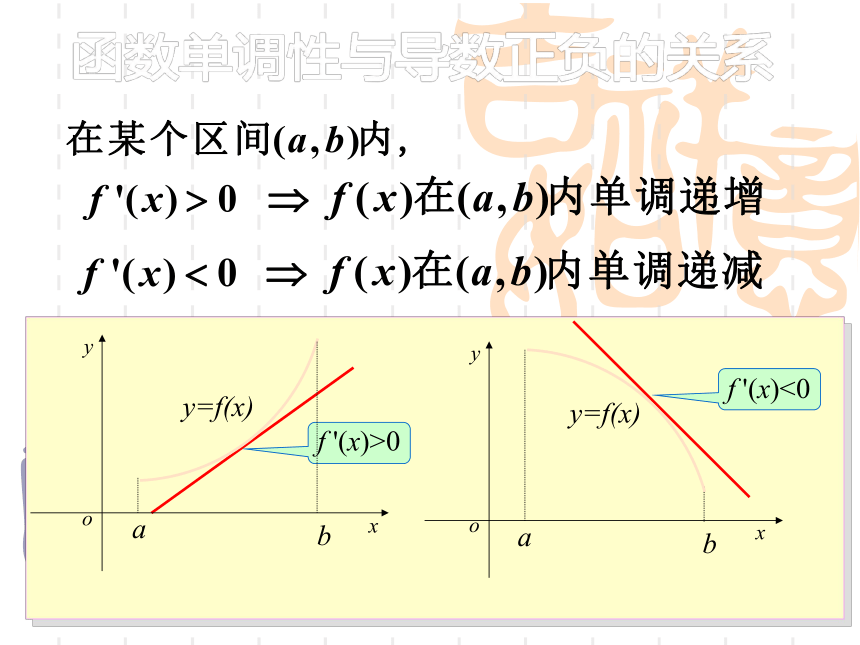
(2)点P处的切线方程.即点P处的切线的斜率等于4. (2)在点P处的切线方程是y-8/3=4(x-2),即12x-3y-16=0.函数单调性与导数正负的关系注意:
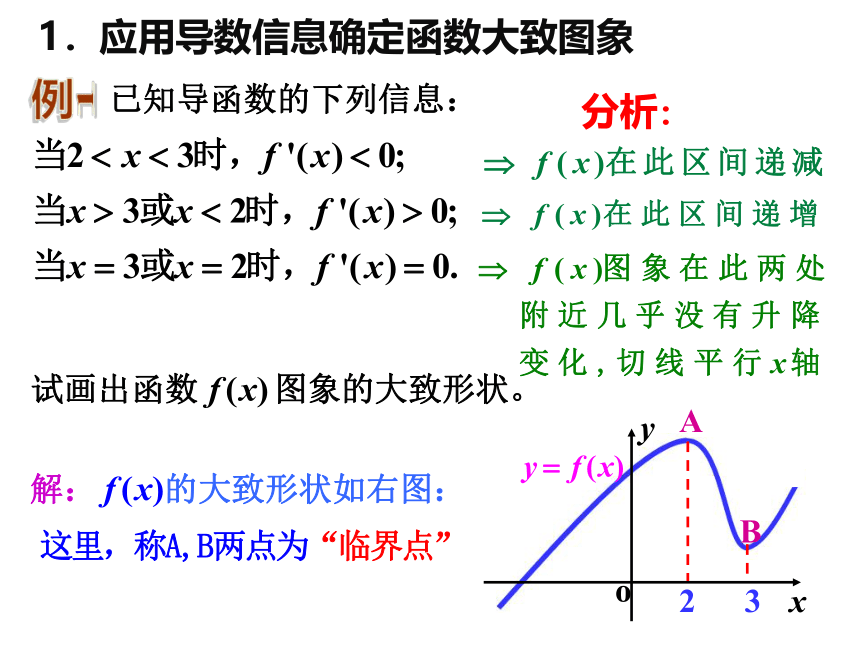
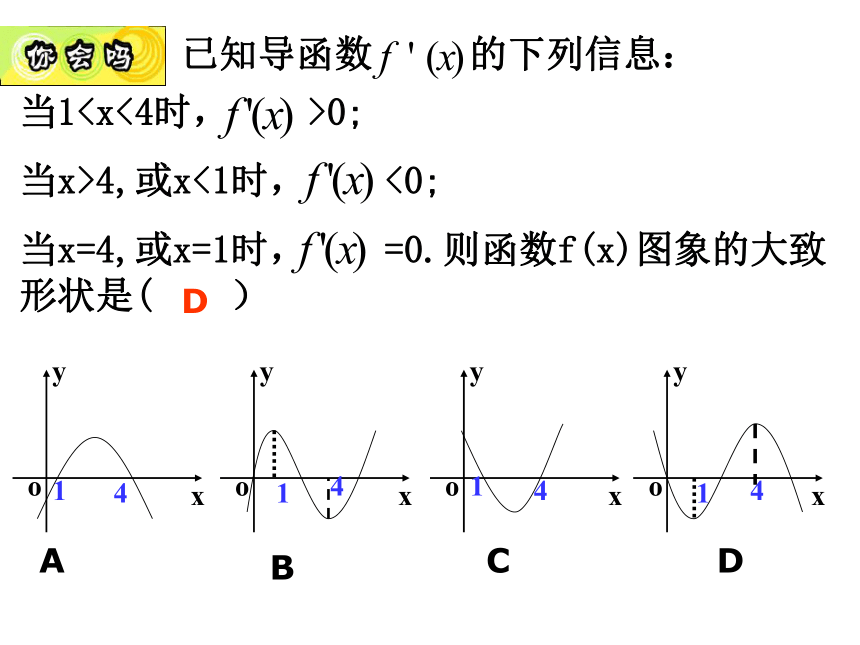
应正确理解 “ 某个区间 ”的含义,它必是定义域内的某个区间。f '(x)>0f '(x)<0已知导函数的下列信息:试画出函数 图象的大致形状。分析:解: 的大致形状如右图:1.应用导数信息确定函数大致图象 已知导函数 的下列信息:当10;
当x>4,或x<1时, <0;
当x=4,或x=1时, =0.则函数f(x)图象的大致形状是( )ABCDD2.求函数 的单调区间。例变1:求函数 的单调区间。解:的单调递增区间为单调递减区间为变2:求函数 的单调区间。巩固提高:解:2.应用导求函数的单调区间2. 利用导数判断、证明函数的单调性?例2 确定函数f(x)=2x3-6x2+7的单调区间解:f′(x)=(2x3-6x2+7)′=6x2-12x令6x2-12x>0,解得x>2或x<0∴f(x)的单调递增区间是(-∞,0),(2,+∞); f(x)的单调递减区间是(0,2)。令6x2-12x<0,解得0<x<2.说明:当函数的单调增区间或减区间有多个时,单调区间之间不能用 连接,只能分开写,或者可用“,”“和”连接。利用导数讨论函数单调的步骤:(2)求导数(1)求 的定义域D例2. 判断下列函数的单调性 ,并求出单调区间
(1)
(2)
(3)
(4)C A B C D-2-1-12-221-21-1-1巩
固定义域R , f ?(x) =x2-x=x(x-1)令x(x-1)>0, 得x<0或x>1,则 f(x)单调 递增区间(-∞,0),(1, +∞)令x(x-1)<0,得0区间(0,1).注意:
求单调区间: 1:首先注意 定义域,
2:其次区间不能用 ( U) 连接(第一步)(第二步)(第三步)一、函数的极值定义设函数f(x)在点x0附近有定义,如果对X0附近的所有点,都有f(x)f(x0), 则f(x0) 是函数f(x)的一个极小值,记作y极小值= f(x0); 函数的极大值与极小值统称为极值.
(极值即峰谷处的值)使函数取得极值的点x0称为极值点例3:求函数y=x4-2x2+5的极大值与极小值.解:令 ,解得x=-1,0,1.随着x的变化, 的变化情况如下表:从上表可知,当x=0时,函数有极大值为5,当x=±1时,函数有极小值为4.(1)令f (x)’>0,得-11;(2)令f (x)’<0,得x <-1 ,或0 求
在 时极值。例 2例 2例4:求函数y=x4-2x2+5在区间[-2,2]上的最大值与最小值.解:令 ,解得x=-1,0,1.在区间[-2,2]上,当x变化时, 的变化情况如下表:从上表可知,当x=±2时,函数有最大值为13,当x=±1时,函数有最小值为4.(1)当f (x)’>0,即x>2,或x<-2时;(2)当f (x)’>0,即-2① f ?(x0)=0,则f (x0)必为极值;
② f (x)= 在x=0 处取极大值0,
③函数的极小值一定小于极大值
④函数的极小值(或极大值)不会多于一个。
⑤函数的极值即为最值结束吗思考①②③④⑤ 个 极值定义
个关键
①函数y=f(x)在极值点处的f ?(x) =0 。
②极值点左右两边的导数必须异号。
个步骤
①确定定义域
②求f ?(x)= 0的根
③并列成表格由f ?(x)在方程f ?(x)=0的根左右的符号,来判断f(x)在这个根处取极值的情况
小 结 莅临指导!
(1)点P处的切线的斜率;
(2)点P处的切线方程.即点P处的切线的斜率等于4. (2)在点P处的切线方程是y-8/3=4(x-2),即12x-3y-16=0.函数单调性与导数正负的关系注意:
应正确理解 “ 某个区间 ”的含义,它必是定义域内的某个区间。f '(x)>0f '(x)<0已知导函数的下列信息:试画出函数 图象的大致形状。分析:解: 的大致形状如右图:1.应用导数信息确定函数大致图象 已知导函数 的下列信息:当1
当x>4,或x<1时, <0;
当x=4,或x=1时, =0.则函数f(x)图象的大致形状是( )ABCDD2.求函数 的单调区间。例变1:求函数 的单调区间。解:的单调递增区间为单调递减区间为变2:求函数 的单调区间。巩固提高:解:2.应用导求函数的单调区间2. 利用导数判断、证明函数的单调性?例2 确定函数f(x)=2x3-6x2+7的单调区间解:f′(x)=(2x3-6x2+7)′=6x2-12x令6x2-12x>0,解得x>2或x<0∴f(x)的单调递增区间是(-∞,0),(2,+∞); f(x)的单调递减区间是(0,2)。令6x2-12x<0,解得0<x<2.说明:当函数的单调增区间或减区间有多个时,单调区间之间不能用 连接,只能分开写,或者可用“,”“和”连接。利用导数讨论函数单调的步骤:(2)求导数(1)求 的定义域D例2. 判断下列函数的单调性 ,并求出单调区间
(1)
(2)
(3)
(4)C A B C D-2-1-12-221-21-1-1巩
固定义域R , f ?(x) =x2-x=x(x-1)令x(x-1)>0, 得x<0或x>1,则 f(x)单调 递增区间(-∞,0),(1, +∞)令x(x-1)<0,得0
求单调区间: 1:首先注意 定义域,
2:其次区间不能用 ( U) 连接(第一步)(第二步)(第三步)一、函数的极值定义设函数f(x)在点x0附近有定义,如果对X0附近的所有点,都有f(x)
(极值即峰谷处的值)使函数取得极值的点x0称为极值点例3:求函数y=x4-2x2+5的极大值与极小值.解:令 ,解得x=-1,0,1.随着x的变化, 的变化情况如下表:从上表可知,当x=0时,函数有极大值为5,当x=±1时,函数有极小值为4.(1)令f (x)’>0,得-1
在 时极值。例 2例 2例4:求函数y=x4-2x2+5在区间[-2,2]上的最大值与最小值.解:令 ,解得x=-1,0,1.在区间[-2,2]上,当x变化时, 的变化情况如下表:从上表可知,当x=±2时,函数有最大值为13,当x=±1时,函数有最小值为4.(1)当f (x)’>0,即x>2,或x<-2时;(2)当f (x)’>0,即-2
② f (x)= 在x=0 处取极大值0,
③函数的极小值一定小于极大值
④函数的极小值(或极大值)不会多于一个。
⑤函数的极值即为最值结束吗思考①②③④⑤ 个 极值定义
个关键
①函数y=f(x)在极值点处的f ?(x) =0 。
②极值点左右两边的导数必须异号。
个步骤
①确定定义域
②求f ?(x)= 0的根
③并列成表格由f ?(x)在方程f ?(x)=0的根左右的符号,来判断f(x)在这个根处取极值的情况
小 结 莅临指导!
