3.1.1 函数的图象变换37张PPT
文档属性
| 名称 | 3.1.1 函数的图象变换37张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-19 17:52:26 | ||
图片预览







文档简介
课件37张PPT。函数的图象变换华罗庚
数少形时少直观
形少数时难入微
数形结合百般好
数形分离万事休
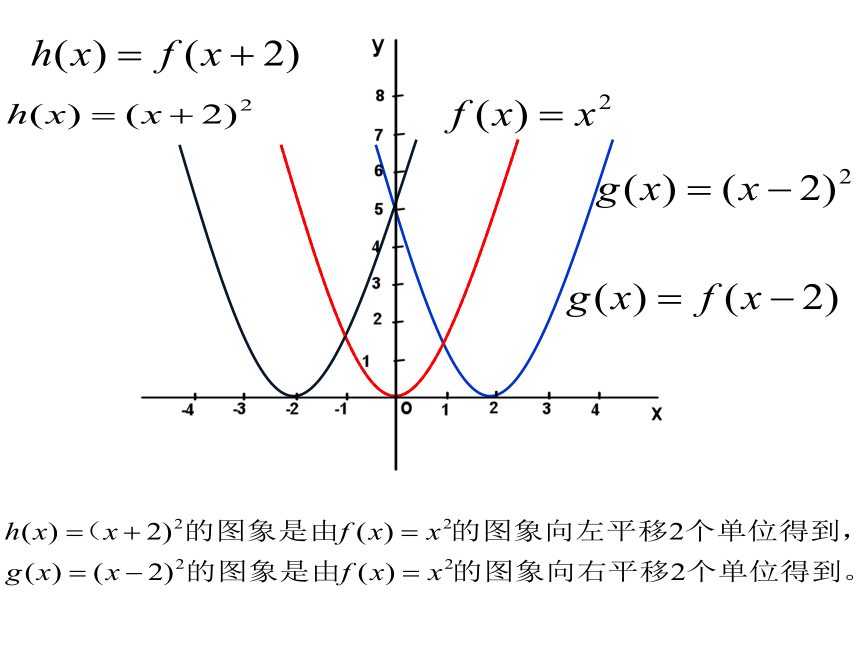
引入:前面我们学习了指数函数、对数函数的图象和性质,其中涉及到许多与图象有关的问题或利用函数图象(数形结合)来解决的问题。其实,在初中就涉及到函数图象的平移问题。今天我们就来梳理一下函数图象的变换问题。有关数形结合的重要性我国著名数学家华罗庚早有论断下面我们就从具体的实例出发,利用特殊到一般的思想总结函数图象变换的规律,并学习其简单的应用。例1.画出下列函数的图象, 并说明它们的关系:
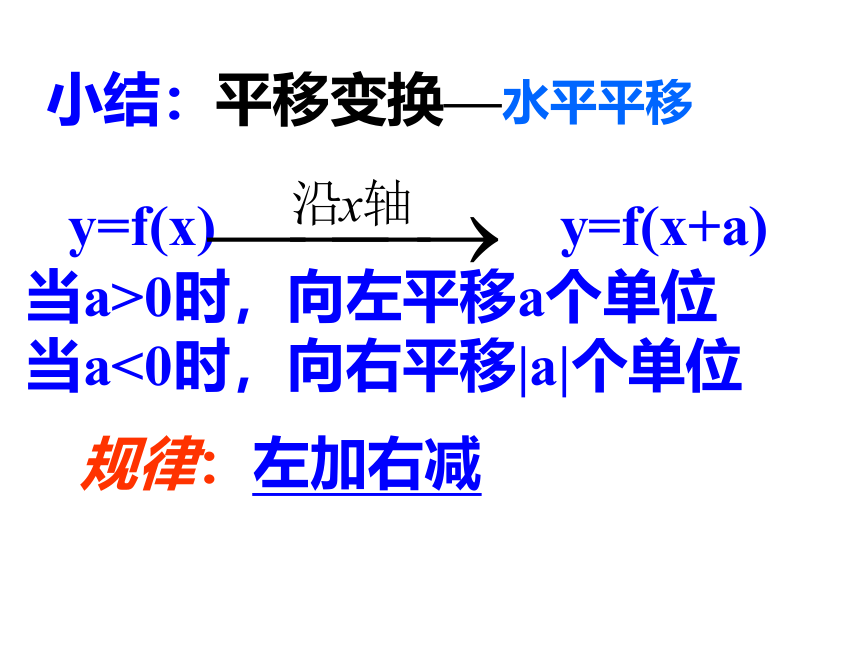
(1) f(x)=x2(2) g(x)=(x+2)2(3) h(x)=(x-2)2规律:左加右减平移变换—水平平移 y=f(x) y=f(x+a) 当a>0时,向左平移a个单位 当a<0时,向右平移|a|个单位 小结:例2:画出下列函数的图象, 并说明它们的关系:
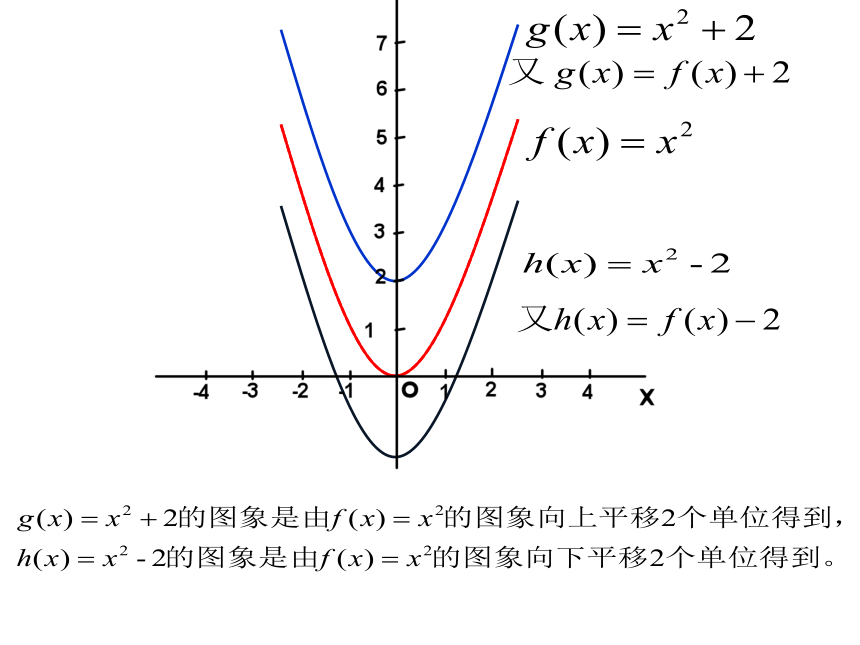
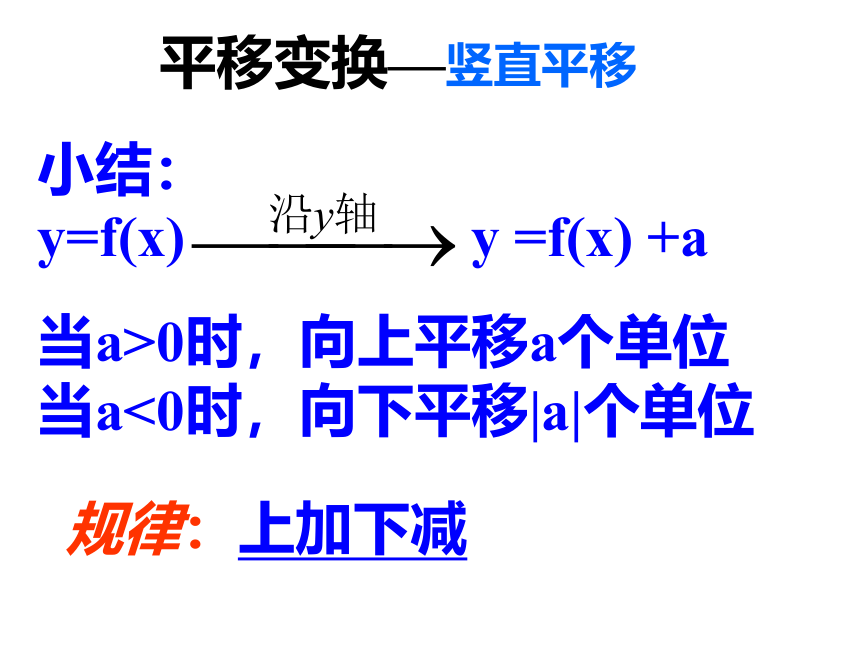
(1) f(x)=x2(2) g(x)=x2+2(3) h(x)=x2-2规律:上加下减小结: y=f(x) y =f(x) +a
当a>0时,向上平移a个单位当a<0时,向下平移|a|个单位 平移变换—竖直平移练习:
的图象变化得到?此函数的对称中心是什么?分析:一次分式函数是由反比例函数经过平移得到。那如何得到平移过程呢?常数分离!!!观察下面指数函数的图象一般地,y=f(x)与y=f(-x)的图象关于 对称; y轴点(-X,Y)与(X,Y)
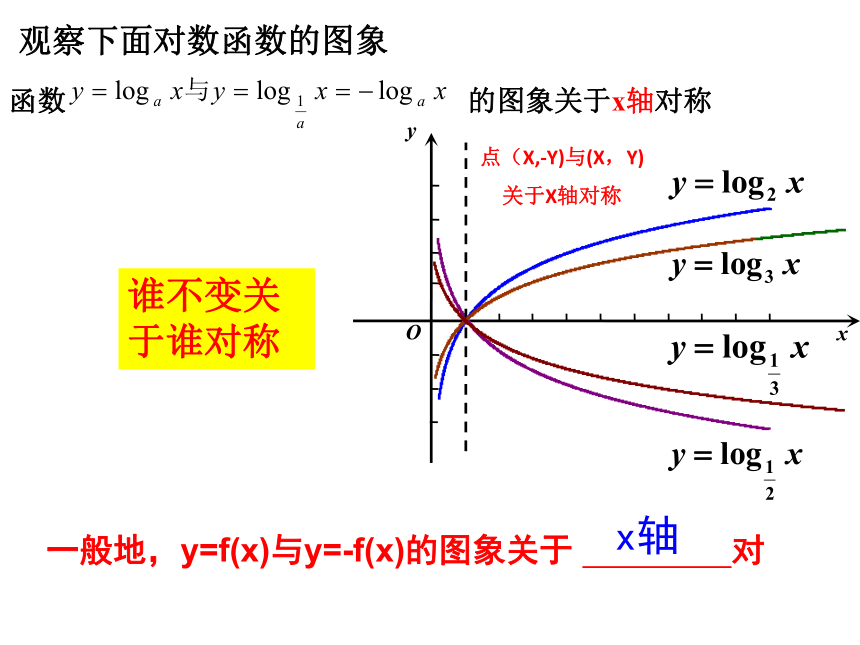
关于Y轴对称谁不变关于谁对称观察下面对数函数的图象函数 的图象关于x轴对称点(X,-Y)与(X,Y)
关于X轴对称一般地,y=f(x)与y=-f(x)的图象关于 对称; x轴谁不变关于谁对称例3.①画函数 并说明
由 的图像怎样变换而得到?②画函数并说由 的图像怎样变换而得到?例3.①画函数 并说明
由 的图像怎样变换而得到?例3.①画函数 并说明
由 的图像怎样变换而得到?小结: 1、y=f(x)?y=f(|x|),保留y=f(x)图象在y轴右侧部分,并将y=f(x)在y轴右侧部分翻折到y轴左侧。 2、 y=f(x)?y=|f(x)|,将y=f(x)图象在x轴下侧部分沿x轴翻折到x轴上侧,并保留x轴上侧部分。翻折变换练习: 函数
的单调增区间为 a>0时向左平移a个单位;a<0时向右平移|a|个单位.a>0时向上平移a个单位;a<0时向下平移|a|个单位.y=f(-x)与y=f(x)的图象关于y轴对称.y=-f(x)与y=f(x)的图象关于x轴对称.y=-f(-x)与y=f(x)的图象关于原点轴对称.保留y=f(x)图象在y轴右侧部分,将y=f(x)图象在y轴右侧部分沿y轴翻折到y轴左侧。将y=f(x)图象在x轴下侧部分沿x轴翻折到x轴上侧,并保留x轴上侧部分。总结:分析:作函数图象的方法有:列表描点法(列表,描点,连线)和图象变换法(平移变换、对称变换、翻折变换)课堂练习课堂总结: 本节课从特殊到一般的思路学习函数图象的三种变换(平移变换、对称变换、翻折变换)及其应用。利用图象变换解题,关键是理清图象变换的过程,掌握好基本初等函数的图象及变换的实质(要通过具体的实例作为载体来理解掌握三种变换)。在后续的学习中我们将进一步学习它的应用。谢谢!!!
数少形时少直观
形少数时难入微
数形结合百般好
数形分离万事休
引入:前面我们学习了指数函数、对数函数的图象和性质,其中涉及到许多与图象有关的问题或利用函数图象(数形结合)来解决的问题。其实,在初中就涉及到函数图象的平移问题。今天我们就来梳理一下函数图象的变换问题。有关数形结合的重要性我国著名数学家华罗庚早有论断下面我们就从具体的实例出发,利用特殊到一般的思想总结函数图象变换的规律,并学习其简单的应用。例1.画出下列函数的图象, 并说明它们的关系:
(1) f(x)=x2(2) g(x)=(x+2)2(3) h(x)=(x-2)2规律:左加右减平移变换—水平平移 y=f(x) y=f(x+a) 当a>0时,向左平移a个单位 当a<0时,向右平移|a|个单位 小结:例2:画出下列函数的图象, 并说明它们的关系:
(1) f(x)=x2(2) g(x)=x2+2(3) h(x)=x2-2规律:上加下减小结: y=f(x) y =f(x) +a
当a>0时,向上平移a个单位当a<0时,向下平移|a|个单位 平移变换—竖直平移练习:
的图象变化得到?此函数的对称中心是什么?分析:一次分式函数是由反比例函数经过平移得到。那如何得到平移过程呢?常数分离!!!观察下面指数函数的图象一般地,y=f(x)与y=f(-x)的图象关于 对称; y轴点(-X,Y)与(X,Y)
关于Y轴对称谁不变关于谁对称观察下面对数函数的图象函数 的图象关于x轴对称点(X,-Y)与(X,Y)
关于X轴对称一般地,y=f(x)与y=-f(x)的图象关于 对称; x轴谁不变关于谁对称例3.①画函数 并说明
由 的图像怎样变换而得到?②画函数并说由 的图像怎样变换而得到?例3.①画函数 并说明
由 的图像怎样变换而得到?例3.①画函数 并说明
由 的图像怎样变换而得到?小结: 1、y=f(x)?y=f(|x|),保留y=f(x)图象在y轴右侧部分,并将y=f(x)在y轴右侧部分翻折到y轴左侧。 2、 y=f(x)?y=|f(x)|,将y=f(x)图象在x轴下侧部分沿x轴翻折到x轴上侧,并保留x轴上侧部分。翻折变换练习: 函数
的单调增区间为 a>0时向左平移a个单位;a<0时向右平移|a|个单位.a>0时向上平移a个单位;a<0时向下平移|a|个单位.y=f(-x)与y=f(x)的图象关于y轴对称.y=-f(x)与y=f(x)的图象关于x轴对称.y=-f(-x)与y=f(x)的图象关于原点轴对称.保留y=f(x)图象在y轴右侧部分,将y=f(x)图象在y轴右侧部分沿y轴翻折到y轴左侧。将y=f(x)图象在x轴下侧部分沿x轴翻折到x轴上侧,并保留x轴上侧部分。总结:分析:作函数图象的方法有:列表描点法(列表,描点,连线)和图象变换法(平移变换、对称变换、翻折变换)课堂练习课堂总结: 本节课从特殊到一般的思路学习函数图象的三种变换(平移变换、对称变换、翻折变换)及其应用。利用图象变换解题,关键是理清图象变换的过程,掌握好基本初等函数的图象及变换的实质(要通过具体的实例作为载体来理解掌握三种变换)。在后续的学习中我们将进一步学习它的应用。谢谢!!!
