人教版八年级上册课件 14.2.1平方差公式(第一课时)课件(共23张PPT)
文档属性
| 名称 | 人教版八年级上册课件 14.2.1平方差公式(第一课时)课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 620.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-20 08:58:14 | ||
图片预览







文档简介
课件23张PPT。平方差公式
(第一课时) (x + 3)( x+5)=x2+5x+3X+15=x2+8x多项式与多项式是如何相乘的?+15 (a+b)(m+n)=am+an+bm+bn回顾旧知 灰太狼开了租地公司,一天他把一边长为a米的正方形土地租给慢羊羊种植.有一年他对慢羊羊说:“我把这块地的一边增加5米,另一边减少5米,再继续租给你, 你也没吃亏,你看如何?”慢羊羊一听觉得没有吃亏,就答应了.回到羊村,就把这件事对喜羊羊他们讲了,大家一听,都说道:“村长,您吃亏了!” 慢羊羊村长很吃惊…同学们,你能告诉慢羊羊这是为什么吗?
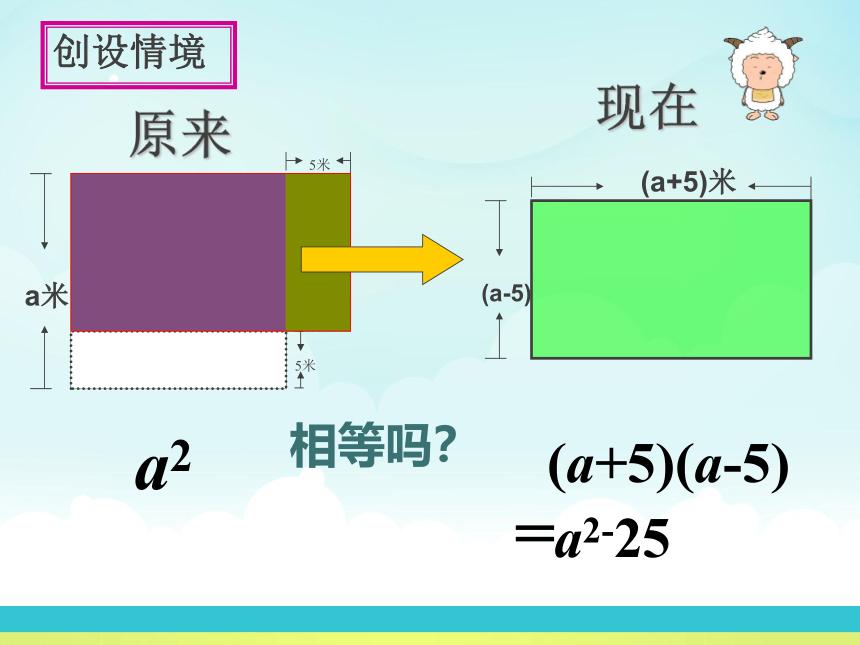
创设情境相等吗?原来现在a2(a+5)(a-5)=a2-25创设情境
(1) = ;
(2) = ;
(3) = .探究平方差公式算一算,比一比,看谁算得又快又准 它们的结果有什么特点?能不能用字母表示你的发现?式子左边具有什么共同特征?
(1) = ;
(2) = ;
(3) = .探究平方差公式算一算,比一比,看谁算得又快又准 它们的结果有什么特点?能不能用字母表示你的发现?式子左边具有什么共同特征?两个数的和与这两个数的差的积,等于这两个数的平方差.(a+b)(a?b)=a2?b214.2.1平方差公式(a+b)(a?b)=a2?b2平方差公式:两个数的和与这两个数的差的积,等于这两个数的平方差.(a+b)(a?b)=a2?b2你能想办法推导出这个公式吗?根据多项式的乘法法则: (a+b)(a-b)
=a2-ab+ab-b2
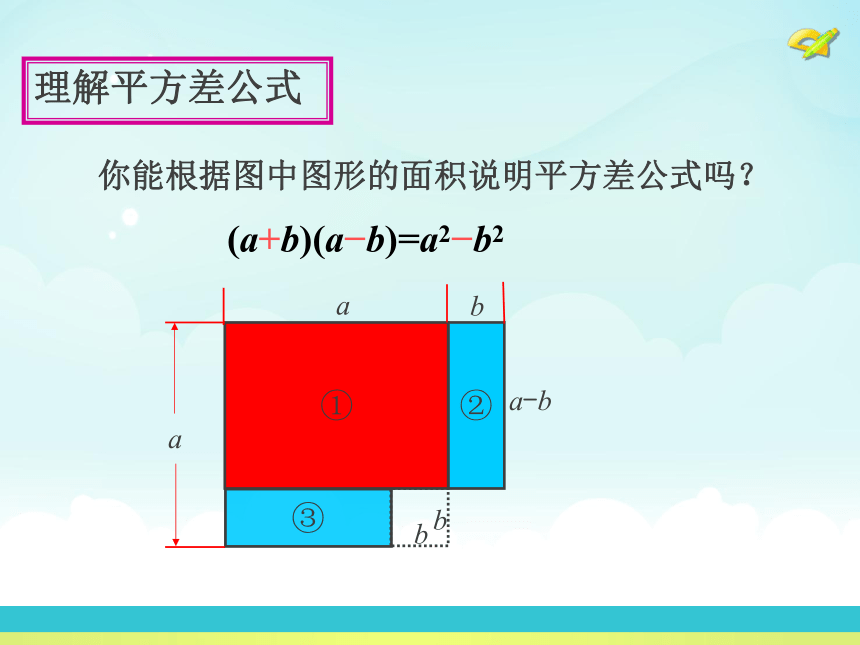
= a2-b2理解平方差公式 你能根据图中图形的面积说明平方差公式吗? 理解平方差公式(a+b)(a?b)=a2?b2(一)、公式的结构特征理解平方差公式1、(a – b ) ( a + b) = a2 - b22、(b + a )( -b + a ) = a2 - b2(a+b)(a?b)=a2?b2理解平方差公式(二)、公式变形注:这里的两数可以是两个单项式 也可以是两个 多项式 .运用平方差公式 解:(1) 运用平方差公式 解:(2) 例2 计算:
(1) 102×98;
(2)(y+2) (y-2) – (y-1) (y+5) .解: (1) 102×98(2) (y+2)(y-2)- (y-1)(y+5) = 1002-22 =1000 – 4 =(100+2)(100-2) =9996 = (y2-22)-(y2+4y-5) = y2-4-y2-4y+5 = - 4y + 1.运用平方差公式(1)(2b+a)(a-2b)=4b2 - a2 ( ) (2)(m–n )(-m -n)=-m2 - n2 ( ) (3)(x+ y) (-x -y)=x2 - y2 ( ) (4)(a-b+c)(a-b-c)= (a-b)2- c2 ( √ )a2 -4b2n2 -m2-x2-2xy -y2×××(5)(3b+2a)(2a-3b)=4a2 - 9b2 ( ) √巩固平方差公式练习1 下面各式的计算对不对?如果不对,应当怎样改正? 从例题1和练习1中,你认为运用公式解决问题时应注意什么?总结经验(一)、公式的结构特征(a+b)(a?b)=a2?b2(二)、公式变形1、(a – b ) ( a + b) = a2 - b22、(b + a )( -b + a ) = a2 - b2适当交换合理加括号公式中字母可以是具体数字,也可以是单项式或多项式。
(1)本节课学习了哪些主要内容?
(2)应用平方差公式时要注意什么?课堂小结两个数的和与这两个数的差的积,等于这两个数的平方差. 教科书习题14.2第1题. 布置作业1.计算 20042 - 2003×2005;解:
20042 - 2003×2005= 20042 - (2004-1)(2004+1)= 20042- (20042-12 )= 20042- 20042+12 =12、利用平方差公式计算:(a-2)(a+2)(a2 + 4)
解:原式=(a2-4)(a2+4)
=a4-16
( )3.化简(x4+y4 )(x4+y4 )(x4+y4)知难而进goodbye!
(1) = ;
(2) = ;
(3) = .探究平方差公式算一算,比一比,看谁算得又快又准 它们的结果有什么特点?能不能用字母表示你的发现?式子左边具有什么共同特征?
(1) = ;
(2) = ;
(3) = .探究平方差公式算一算,比一比,看谁算得又快又准 它们的结果有什么特点?能不能用字母表示你的发现?式子左边具有什么共同特征?两个数的和与这两个数的差的积,等于这两个数的平方差.(a+b)(a?b)=a2?b214.2.1平方差公式(a+b)(a?b)=a2?b2平方差公式:两个数的和与这两个数的差的积,等于这两个数的平方差.(a+b)(a?b)=a2?b2你能想办法推导出这个公式吗?根据多项式的乘法法则: (a+b)(a-b)
=a2-ab+ab-b2
= a2-b2理解平方差公式 你能根据图中图形的面积说明平方差公式吗? 理解平方差公式(a+b)(a?b)=a2?b2(一)、公式的结构特征理解平方差公式1、(a – b ) ( a + b) = a2 - b22、(b + a )( -b + a ) = a2 - b2(a+b)(a?b)=a2?b2理解平方差公式(二)、公式变形注:这里的两数可以是两个单项式 也可以是两个 多项式 .运用平方差公式 解:(1) 运用平方差公式 解:(2) 例2 计算:
(1) 102×98;
(2)(y+2) (y-2) – (y-1) (y+5) .解: (1) 102×98(2) (y+2)(y-2)- (y-1)(y+5) = 1002-22 =1000 – 4 =(100+2)(100-2) =9996 = (y2-22)-(y2+4y-5) = y2-4-y2-4y+5 = - 4y + 1.运用平方差公式(1)(2b+a)(a-2b)=4b2 - a2 ( ) (2)(m–n )(-m -n)=-m2 - n2 ( ) (3)(x+ y) (-x -y)=x2 - y2 ( ) (4)(a-b+c)(a-b-c)= (a-b)2- c2 ( √ )a2 -4b2n2 -m2-x2-2xy -y2×××(5)(3b+2a)(2a-3b)=4a2 - 9b2 ( ) √巩固平方差公式练习1 下面各式的计算对不对?如果不对,应当怎样改正? 从例题1和练习1中,你认为运用公式解决问题时应注意什么?总结经验(一)、公式的结构特征(a+b)(a?b)=a2?b2(二)、公式变形1、(a – b ) ( a + b) = a2 - b22、(b + a )( -b + a ) = a2 - b2适当交换合理加括号公式中字母可以是具体数字,也可以是单项式或多项式。
(1)本节课学习了哪些主要内容?
(2)应用平方差公式时要注意什么?课堂小结两个数的和与这两个数的差的积,等于这两个数的平方差. 教科书习题14.2第1题. 布置作业1.计算 20042 - 2003×2005;解:
20042 - 2003×2005= 20042 - (2004-1)(2004+1)= 20042- (20042-12 )= 20042- 20042+12 =12、利用平方差公式计算:(a-2)(a+2)(a2 + 4)
解:原式=(a2-4)(a2+4)
=a4-16
( )3.化简(x4+y4 )(x4+y4 )(x4+y4)知难而进goodbye!
