人教版八年级上册课件 第十四章 14.1.3 积的乘方课件 (共26张PPT)
文档属性
| 名称 | 人教版八年级上册课件 第十四章 14.1.3 积的乘方课件 (共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 629.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-20 00:00:00 | ||
图片预览


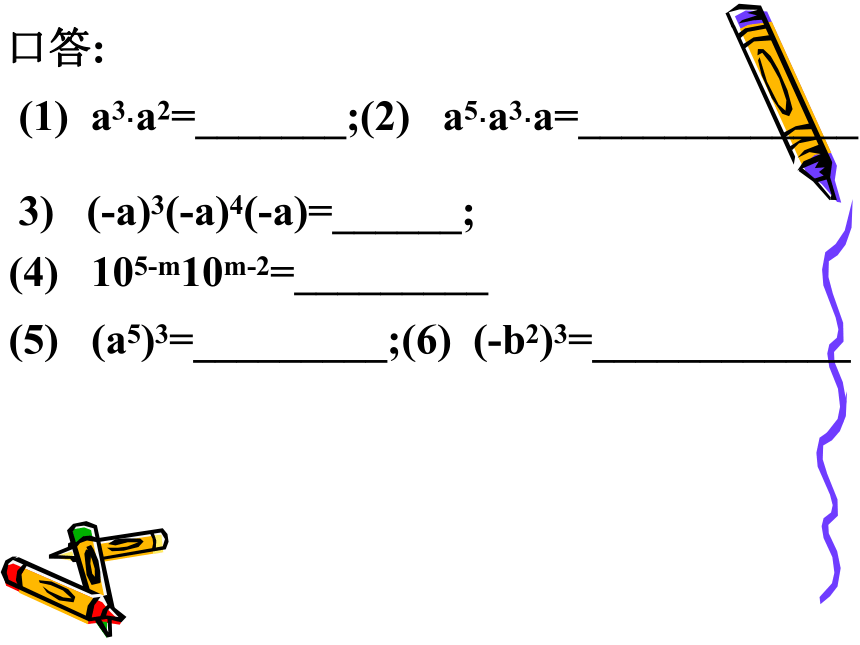






文档简介
课件26张PPT。积的乘方回顾与思考?幂的意义:an=am+n(m,n都是正整数)(am)n= (m、n都是正整数)amn口答:(1) a3·a2=_______;(2) a5·a3·a=_____________;3) (-a)3(-a)4(-a)=______;(4) 105-m10m-2=_________(5) (a5)3=_________;(6) (-b2)3=____________ 一个立方体的棱长为5,那么立方体的体积是多少?如果棱长为 ,那么立方体的体积是 ?怎样计算? 解:=? 计算:
(3×4)2与32 × 42,你会发现什么?填空:122 144 9×16144 =结论:(3×4)2与32 × 42相等×33__________________________nn44⒈⒉⒊n个合作交流类比与猜想:
(ab)3与a3b3 是什么关系呢?(ab)3=(ab)·(ab)·(ab)=(aaa) ·(bbb)= a3b3 积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.(n为正整数) (n为正整数)例题解析例题解析 【例1】计算:
(1) (3x)2 ; (2)(-2b)5 ;
(3) (-2xy)4 ; (4)(3a2)n . 例题解析例题解析【例2】计算:
(1)(3x)2 ; (2)(-2b)5 ; (3)(-2xy)4 ; (4)(3a2)n . =32x2 = 9x2 ;(1) (3x)2解:(2) (-2b)5 = (-2)5b5 = -32b25 ;(3) (-2xy)4 = (-2x)4 y4= (-2)4 x4 y4 (4) (3a2)n = 3n (a2)n = 3n a2n 。=16x4 y4 ;练习1判断正误: ( )( )( )( )例2计算下列各式,并把结果用幂的形式表示: (1)(2)(4)(3)(5)(6)计算:
(1)
(2)(3)挑战自我能力提升如果(an?bm?b)3=a9b15,求m, n的值练习6:公 式 的 反 向 使 用(ab)n = an·bn (m,n都是正整数)反向使用:an·bn = (ab)n 计算:
(1)(2)能力升级解:(1)(2)
练习: (2) (-5)16 × (-2)15 计算:
2(x3)2 · x3-(3x3)3+(5x)2 ·x7解:原式=2x6 · x3-27x9+25x2 ·x7 注意:运算顺序是先乘方,再乘除, 最后算加减。=2x9-27x9+25x9=0练习4:(0.04)2004×[(-5)2004]2=?=(0.22)2004 × 54008=(0.2)4008 × 54008=(0.2 ×5)4008=14008解法一: (0.04)2004×[(-5)2004]2=1练习5:探讨--如何计算简便?=(0.04)2004 × [(-5)2]2004=(0.04×25)2004=12004=1= (0.04)2004 ×(25)2004 解法二: (0.04)2004×[(-5)2004]2小结:
1、本节课的主要内容:
am·an=am+n (am)n=amn
(ab)n=anbn ( m、n都是正整数)2、 运用积的乘方法则时要注意什么? 公式中的a、b代表任何代数式;每一个因式 都要“乘方”;注意结果的符号、幂指数及其逆向运用。(混合运算要注意运算顺序)积的乘方幂的运算的三条重要性质:谈谈本节课你有何收获?小结积的乘方法则及逆运算。
积的乘方给解决实际问题带来简便。
幂的混合运算。
再 见
(3×4)2与32 × 42,你会发现什么?填空:122 144 9×16144 =结论:(3×4)2与32 × 42相等×33__________________________nn44⒈⒉⒊n个合作交流类比与猜想:
(ab)3与a3b3 是什么关系呢?(ab)3=(ab)·(ab)·(ab)=(aaa) ·(bbb)= a3b3 积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.(n为正整数) (n为正整数)例题解析例题解析 【例1】计算:
(1) (3x)2 ; (2)(-2b)5 ;
(3) (-2xy)4 ; (4)(3a2)n . 例题解析例题解析【例2】计算:
(1)(3x)2 ; (2)(-2b)5 ; (3)(-2xy)4 ; (4)(3a2)n . =32x2 = 9x2 ;(1) (3x)2解:(2) (-2b)5 = (-2)5b5 = -32b25 ;(3) (-2xy)4 = (-2x)4 y4= (-2)4 x4 y4 (4) (3a2)n = 3n (a2)n = 3n a2n 。=16x4 y4 ;练习1判断正误: ( )( )( )( )例2计算下列各式,并把结果用幂的形式表示: (1)(2)(4)(3)(5)(6)计算:
(1)
(2)(3)挑战自我能力提升如果(an?bm?b)3=a9b15,求m, n的值练习6:公 式 的 反 向 使 用(ab)n = an·bn (m,n都是正整数)反向使用:an·bn = (ab)n 计算:
(1)(2)能力升级解:(1)(2)
练习: (2) (-5)16 × (-2)15 计算:
2(x3)2 · x3-(3x3)3+(5x)2 ·x7解:原式=2x6 · x3-27x9+25x2 ·x7 注意:运算顺序是先乘方,再乘除, 最后算加减。=2x9-27x9+25x9=0练习4:(0.04)2004×[(-5)2004]2=?=(0.22)2004 × 54008=(0.2)4008 × 54008=(0.2 ×5)4008=14008解法一: (0.04)2004×[(-5)2004]2=1练习5:探讨--如何计算简便?=(0.04)2004 × [(-5)2]2004=(0.04×25)2004=12004=1= (0.04)2004 ×(25)2004 解法二: (0.04)2004×[(-5)2004]2小结:
1、本节课的主要内容:
am·an=am+n (am)n=amn
(ab)n=anbn ( m、n都是正整数)2、 运用积的乘方法则时要注意什么? 公式中的a、b代表任何代数式;每一个因式 都要“乘方”;注意结果的符号、幂指数及其逆向运用。(混合运算要注意运算顺序)积的乘方幂的运算的三条重要性质:谈谈本节课你有何收获?小结积的乘方法则及逆运算。
积的乘方给解决实际问题带来简便。
幂的混合运算。
再 见
