常见金属晶体的结构[上学期]
文档属性
| 名称 | 常见金属晶体的结构[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 87.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 化学 | ||
| 更新时间 | 2006-10-30 15:35:00 | ||
图片预览








文档简介
课件24张PPT。第五讲:
常见金属晶体的结构
主要内容包括:
1. 晶体结构的密堆积原理
2. 金属键的本质和金属的一般性质
3. 合金的结构一、晶体结构的密堆积原理
所谓密堆积结构是指在由无方向性的
金属键力、离子键力及范德华力等结合力
的晶体中, 原子、离子或分子等微粒总是倾
向于采取相互配位数高、能充分利用空间
的堆积密度大的那些结构。这样的结构由
于充分利用了空间, 从而使体系的势能尽可
能降低, 使体系稳定。这就是密堆积原理。1. 面心立方(A1)和六方 (A3)最密堆积
A1和A3堆积的异同
A1是ABCABCABC······型式的堆积,从
这种堆积中可以抽出一个立方面心点阵,因
此这种堆积型式的最小单位是一个立方面心
晶胞。
A3是ABABABAB······型式的堆积,这种
堆积型式的最小单位是一个六方晶胞。A1和A3堆积形成晶胞的两要素
A1堆积晶胞是立方面心, 因此
晶胞的大小可以用等径圆球的半径r
表示出来, 即晶胞的边长a与r的关系
为:
该晶胞中有4个圆球, 各个圆球的分
数坐标分别为: A1和A3堆积形成晶胞的两要素
A3堆积晶胞是六晶胞, 因此
晶胞的大小可以用等径圆球的半径r
表示出来, 即晶胞的边长a,c与r的关
系为:
该晶胞中有2个圆球, 各个圆球的分
数坐标分别为: 空间利用率的计算:
A1堆积用圆球半径r表示的晶胞体积为:空间利用率的计算:
A3堆积用圆球半径r表示的晶胞体积为:正四面体空隙、正八面体空隙及多少
A1堆积中, 每个晶胞正四面体空隙、正八面
体空隙及圆球的个数分别为: 8, 4, 4, 即它们的比
是2:1:1。
A3堆积中, 每个晶胞正四面体空隙、正八面
体空隙及圆球的个数分别为: 4, 2, 2, 即它们的比
也是2:1:1。
金属半径与晶胞参数的关系A2堆积形成晶胞的两要素
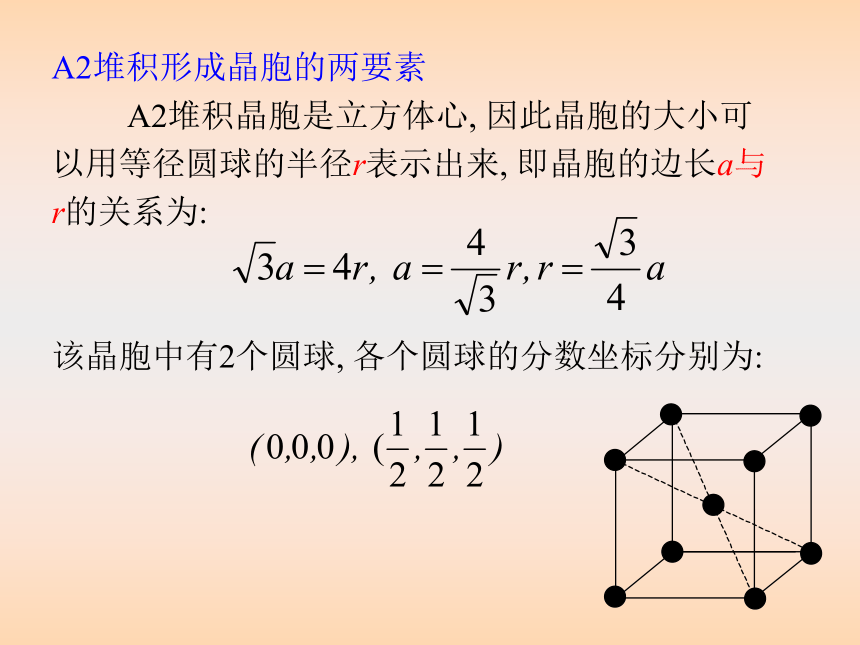
A2堆积晶胞是立方体心, 因此晶胞的大小可
以用等径圆球的半径r表示出来, 即晶胞的边长a与
r的关系为:
该晶胞中有2个圆球, 各个圆球的分数坐标分别为: A2堆积的空间利用率的计算:
A2堆积用圆球半径r表示的晶胞体积为:A4堆积形成晶胞的两要素
A4堆积晶胞是立方面心点阵结构, 因此晶胞
的大小可以用等径圆球的半径r表示出来, 即晶胞
的边长a与r的关系为:
该晶胞中有8个圆球, 各个圆球的分数坐标分别为: A4堆积的空间利用率的计算:
A4堆积用圆球半径r表示的晶胞体积为:常见金属的堆积型式:
碱金属元素一般都是A2型堆积;
碱土金属元素中Be,Mg属于A3型堆积;Ca
既有A1也A3型堆积;Ba属于A2型堆积;
Cu,Ag,Au属于A1型堆积;
Zn,Cd属于A3型堆积;
Ge,Sn属于A4型堆积。二、金属键的本质和金属的一般性质
(1)金属键的本质
可以认为, 金属键是由金属原子的价轨
道重叠在一起, 形成遍布于整个金属的离域
轨道, 所有的价电子分布在离域轨道上属于
整个金属所有。由于价电子在离域轨道分
布, 能量降低很多, 从而形成一种强烈的相
互作用, 这就是金属键的本质。 (2)金属键的一般性质及其结构根源
I. 有导带存在, 是良好的导体;
II. 由于自由电子存在具有良好的传热性能;
III.自由电子能够吸收可见光并能随时放出, 使
金属不透明, 且有光泽;
IV. 等径圆球的堆积使原子间容易滑动, 所以金
属具有良好的延展性和可塑性;
V. 金属间能“互溶”, 易形成合金。 三、合金的结构
(1)金属固溶体
填隙式固溶体
置换式固溶体(无限固溶体和有限固溶体)
(2)金属化合物
“正常价化合物”
“电子化合物”练习题:
1. 指出A1型和A3型等径园球密堆积中密置层的方向各在什么方向上。
2. 硅的结构和金刚石相似, Si的共价半径为117pm, 求硅的晶胞参数、晶胞体积和晶体密度。
3. 已知金属钛为六方最密堆积结构, 钛的原子半径为146pm, 若钛为理想的六方晶胞, 试计算其密度。
4. 金属钠为体心立方A2结构, 晶胞参数a=429pm, 试计算钠的金属半径及理论密度。
5. 有一黄铜合金Cu和Zn的质量分数依次为75%,25%, 晶胞的密度为8.9g·cm-3, 晶体属于立方面心结构, 晶胞中含4个原子。Cu和Zn的相对原子质量分别为63.5和65.4, 求:(1)Cu和Zn所占的原子百分数; (2)每个晶胞含合金的质量是多少克; (3)晶胞的体积多大; (4)统计原子的原子半径多大。6. 已知金刚石中C—C键长为1.54×10-10m,那么金刚石的密度为 g/cm3。(相对原子质量:C 12.0)
7. 金属镍(相对原子质量58.7)是立方面心晶格型式,计算其空间利用率(即原子体积占晶体空间的百分率);若金属镍的密度为8.90g/cm3,计算晶体中最临近原子之间的距离;并计算能放入到镍晶体空隙中最大原子半径是多少?
8. SiC是原子晶体,其结构类似金刚石,为C、Si两原子依次相间排列的正四面体型空间网状结构。右图为两个中心重合,各面分别平行的大小两个正方体,其中心为一Si原子,试在小正方体的顶点上画出与Si最近的C的位置,在大正方体的棱上画出与C最近的Si的位置。两大小正方体的边长之比为_______;Si—C—Si的键角为______ (用反三角函数表示);若Si—C键长为a cm,则大正方体边长为_______cm;SiC晶体的密度为______g/cm3。(NA为阿佛加德罗常数,相对原子质量 C.12 Si.28)。
9. (19分)某同学在学习等径球最密堆积(立方最密堆积A1和六方最密堆积A3)后,提出了另一种最密堆积形式Ax。如右图所示为Ax堆积的片层形式,然后第二层就堆积在第一层的空隙上。请根据Ax的堆积形式回答:
(1).计算在片层结构中(如右图所示)球数、空隙数和切点数之比
(2).在Ax堆积中将会形成正八面体空隙和正四面体空隙。请在片层图中画出正八面体空隙(用·表示)和正四面体空隙(用×表示)的投影,并确定球数、
正八面体空隙数和正四面体空隙数之比
(3).指出Ax堆积中小球的配位数 (4). 计算Ax堆积的原子空间利用率。
(5). 计算正八面体和正四面体空隙半径(可填充小球的最大半径,设等径小球的半径为r)。
(6). 已知金属Ni晶体结构为Ax堆积形式,Ni原子半径为124.6pm,计算金属Ni的密度。(Ni的相对原子质量为58.70)
(7). 如果CuH晶体中Cu+的堆积形式为Ax型,H-填充在空隙中,且配位数是4。则H-填充的是哪一类空隙,占有率是多少?
(8). 当该同学将这种Ax堆积形式告诉老师时,老师说Ax就是A1或A3的某一种。你认为是哪一种,为什么? 答案:
1. A1在C3轴方向上, A3在C6轴方向上。
2.
3.
4.
5. (1)设Cu的原子分数(即摩尔分数)为x, 则:
63.5x:65.4(1-x)=0.75:0.25; x=0.755; 1- x=0.245;
(2)4.25×10-25g; (3) 5.0×10-23cm3; (4) 130pm.6.
7.
8. 2:1(2分) arccos (-1/3)(2分) (2分)
(2分) 9. (1).1:1:2(2分)
一个球参与四个空隙,一个空隙由四个球围成;一个球参与四个切点,一个切点由二个球共用。
(2).图略,正八面体中心投影为平面◇空隙中心,正四面体中心投影为平面切点
1:1:2(2分)
一个球参与六个正八面体空隙,一个正八面体空隙由四个球围成;一个球参与八个正四面体空隙,一个正四面体空隙由四个球围成。
(3).小球的配位数为12(1分)
平面已配位4个,中心球周围的四个空隙上下各堆积4个,共12个。
(4).74.05%(3分) 以4个相邻小球中心构成底面,空隙上小球的中心为上底面的中心构成正四棱柱,设小球半径为r,则正四棱柱边长为2r,高为r,共包括1个小球(4个1/4,1个1/2),空间利用率为
(5).正八面体空隙为0.414r,正四面体空隙为0.225r。(4分)
(6). 8.91g/cm3(3分)
(7). H-填充在正四面体空隙,占有率为50%(2分)
正四面体为4配位,正八面体为6配位,且正四面体空隙数为小球数的2倍。
(8).Ax就是A1,取一个中心小球周围的4个小球的中心为顶点构成正方形,然后上面再取两层,就是顶点面心的堆积形式。底面一层和第三层中心小球是面心,周围四小球是顶点,第二层四小球(四个空隙上)是侧面心。(2分)
常见金属晶体的结构
主要内容包括:
1. 晶体结构的密堆积原理
2. 金属键的本质和金属的一般性质
3. 合金的结构一、晶体结构的密堆积原理
所谓密堆积结构是指在由无方向性的
金属键力、离子键力及范德华力等结合力
的晶体中, 原子、离子或分子等微粒总是倾
向于采取相互配位数高、能充分利用空间
的堆积密度大的那些结构。这样的结构由
于充分利用了空间, 从而使体系的势能尽可
能降低, 使体系稳定。这就是密堆积原理。1. 面心立方(A1)和六方 (A3)最密堆积
A1和A3堆积的异同
A1是ABCABCABC······型式的堆积,从
这种堆积中可以抽出一个立方面心点阵,因
此这种堆积型式的最小单位是一个立方面心
晶胞。
A3是ABABABAB······型式的堆积,这种
堆积型式的最小单位是一个六方晶胞。A1和A3堆积形成晶胞的两要素
A1堆积晶胞是立方面心, 因此
晶胞的大小可以用等径圆球的半径r
表示出来, 即晶胞的边长a与r的关系
为:
该晶胞中有4个圆球, 各个圆球的分
数坐标分别为: A1和A3堆积形成晶胞的两要素
A3堆积晶胞是六晶胞, 因此
晶胞的大小可以用等径圆球的半径r
表示出来, 即晶胞的边长a,c与r的关
系为:
该晶胞中有2个圆球, 各个圆球的分
数坐标分别为: 空间利用率的计算:
A1堆积用圆球半径r表示的晶胞体积为:空间利用率的计算:
A3堆积用圆球半径r表示的晶胞体积为:正四面体空隙、正八面体空隙及多少
A1堆积中, 每个晶胞正四面体空隙、正八面
体空隙及圆球的个数分别为: 8, 4, 4, 即它们的比
是2:1:1。
A3堆积中, 每个晶胞正四面体空隙、正八面
体空隙及圆球的个数分别为: 4, 2, 2, 即它们的比
也是2:1:1。
金属半径与晶胞参数的关系A2堆积形成晶胞的两要素
A2堆积晶胞是立方体心, 因此晶胞的大小可
以用等径圆球的半径r表示出来, 即晶胞的边长a与
r的关系为:
该晶胞中有2个圆球, 各个圆球的分数坐标分别为: A2堆积的空间利用率的计算:
A2堆积用圆球半径r表示的晶胞体积为:A4堆积形成晶胞的两要素
A4堆积晶胞是立方面心点阵结构, 因此晶胞
的大小可以用等径圆球的半径r表示出来, 即晶胞
的边长a与r的关系为:
该晶胞中有8个圆球, 各个圆球的分数坐标分别为: A4堆积的空间利用率的计算:
A4堆积用圆球半径r表示的晶胞体积为:常见金属的堆积型式:
碱金属元素一般都是A2型堆积;
碱土金属元素中Be,Mg属于A3型堆积;Ca
既有A1也A3型堆积;Ba属于A2型堆积;
Cu,Ag,Au属于A1型堆积;
Zn,Cd属于A3型堆积;
Ge,Sn属于A4型堆积。二、金属键的本质和金属的一般性质
(1)金属键的本质
可以认为, 金属键是由金属原子的价轨
道重叠在一起, 形成遍布于整个金属的离域
轨道, 所有的价电子分布在离域轨道上属于
整个金属所有。由于价电子在离域轨道分
布, 能量降低很多, 从而形成一种强烈的相
互作用, 这就是金属键的本质。 (2)金属键的一般性质及其结构根源
I. 有导带存在, 是良好的导体;
II. 由于自由电子存在具有良好的传热性能;
III.自由电子能够吸收可见光并能随时放出, 使
金属不透明, 且有光泽;
IV. 等径圆球的堆积使原子间容易滑动, 所以金
属具有良好的延展性和可塑性;
V. 金属间能“互溶”, 易形成合金。 三、合金的结构
(1)金属固溶体
填隙式固溶体
置换式固溶体(无限固溶体和有限固溶体)
(2)金属化合物
“正常价化合物”
“电子化合物”练习题:
1. 指出A1型和A3型等径园球密堆积中密置层的方向各在什么方向上。
2. 硅的结构和金刚石相似, Si的共价半径为117pm, 求硅的晶胞参数、晶胞体积和晶体密度。
3. 已知金属钛为六方最密堆积结构, 钛的原子半径为146pm, 若钛为理想的六方晶胞, 试计算其密度。
4. 金属钠为体心立方A2结构, 晶胞参数a=429pm, 试计算钠的金属半径及理论密度。
5. 有一黄铜合金Cu和Zn的质量分数依次为75%,25%, 晶胞的密度为8.9g·cm-3, 晶体属于立方面心结构, 晶胞中含4个原子。Cu和Zn的相对原子质量分别为63.5和65.4, 求:(1)Cu和Zn所占的原子百分数; (2)每个晶胞含合金的质量是多少克; (3)晶胞的体积多大; (4)统计原子的原子半径多大。6. 已知金刚石中C—C键长为1.54×10-10m,那么金刚石的密度为 g/cm3。(相对原子质量:C 12.0)
7. 金属镍(相对原子质量58.7)是立方面心晶格型式,计算其空间利用率(即原子体积占晶体空间的百分率);若金属镍的密度为8.90g/cm3,计算晶体中最临近原子之间的距离;并计算能放入到镍晶体空隙中最大原子半径是多少?
8. SiC是原子晶体,其结构类似金刚石,为C、Si两原子依次相间排列的正四面体型空间网状结构。右图为两个中心重合,各面分别平行的大小两个正方体,其中心为一Si原子,试在小正方体的顶点上画出与Si最近的C的位置,在大正方体的棱上画出与C最近的Si的位置。两大小正方体的边长之比为_______;Si—C—Si的键角为______ (用反三角函数表示);若Si—C键长为a cm,则大正方体边长为_______cm;SiC晶体的密度为______g/cm3。(NA为阿佛加德罗常数,相对原子质量 C.12 Si.28)。
9. (19分)某同学在学习等径球最密堆积(立方最密堆积A1和六方最密堆积A3)后,提出了另一种最密堆积形式Ax。如右图所示为Ax堆积的片层形式,然后第二层就堆积在第一层的空隙上。请根据Ax的堆积形式回答:
(1).计算在片层结构中(如右图所示)球数、空隙数和切点数之比
(2).在Ax堆积中将会形成正八面体空隙和正四面体空隙。请在片层图中画出正八面体空隙(用·表示)和正四面体空隙(用×表示)的投影,并确定球数、
正八面体空隙数和正四面体空隙数之比
(3).指出Ax堆积中小球的配位数 (4). 计算Ax堆积的原子空间利用率。
(5). 计算正八面体和正四面体空隙半径(可填充小球的最大半径,设等径小球的半径为r)。
(6). 已知金属Ni晶体结构为Ax堆积形式,Ni原子半径为124.6pm,计算金属Ni的密度。(Ni的相对原子质量为58.70)
(7). 如果CuH晶体中Cu+的堆积形式为Ax型,H-填充在空隙中,且配位数是4。则H-填充的是哪一类空隙,占有率是多少?
(8). 当该同学将这种Ax堆积形式告诉老师时,老师说Ax就是A1或A3的某一种。你认为是哪一种,为什么? 答案:
1. A1在C3轴方向上, A3在C6轴方向上。
2.
3.
4.
5. (1)设Cu的原子分数(即摩尔分数)为x, 则:
63.5x:65.4(1-x)=0.75:0.25; x=0.755; 1- x=0.245;
(2)4.25×10-25g; (3) 5.0×10-23cm3; (4) 130pm.6.
7.
8. 2:1(2分) arccos (-1/3)(2分) (2分)
(2分) 9. (1).1:1:2(2分)
一个球参与四个空隙,一个空隙由四个球围成;一个球参与四个切点,一个切点由二个球共用。
(2).图略,正八面体中心投影为平面◇空隙中心,正四面体中心投影为平面切点
1:1:2(2分)
一个球参与六个正八面体空隙,一个正八面体空隙由四个球围成;一个球参与八个正四面体空隙,一个正四面体空隙由四个球围成。
(3).小球的配位数为12(1分)
平面已配位4个,中心球周围的四个空隙上下各堆积4个,共12个。
(4).74.05%(3分) 以4个相邻小球中心构成底面,空隙上小球的中心为上底面的中心构成正四棱柱,设小球半径为r,则正四棱柱边长为2r,高为r,共包括1个小球(4个1/4,1个1/2),空间利用率为
(5).正八面体空隙为0.414r,正四面体空隙为0.225r。(4分)
(6). 8.91g/cm3(3分)
(7). H-填充在正四面体空隙,占有率为50%(2分)
正四面体为4配位,正八面体为6配位,且正四面体空隙数为小球数的2倍。
(8).Ax就是A1,取一个中心小球周围的4个小球的中心为顶点构成正方形,然后上面再取两层,就是顶点面心的堆积形式。底面一层和第三层中心小球是面心,周围四小球是顶点,第二层四小球(四个空隙上)是侧面心。(2分)
