2018年高中数学新人教B版选修1-1课件:第二章圆锥曲线与方程2.1.2椭圆的几何性质课件(17张)
文档属性
| 名称 | 2018年高中数学新人教B版选修1-1课件:第二章圆锥曲线与方程2.1.2椭圆的几何性质课件(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 135.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-21 00:00:00 | ||
图片预览





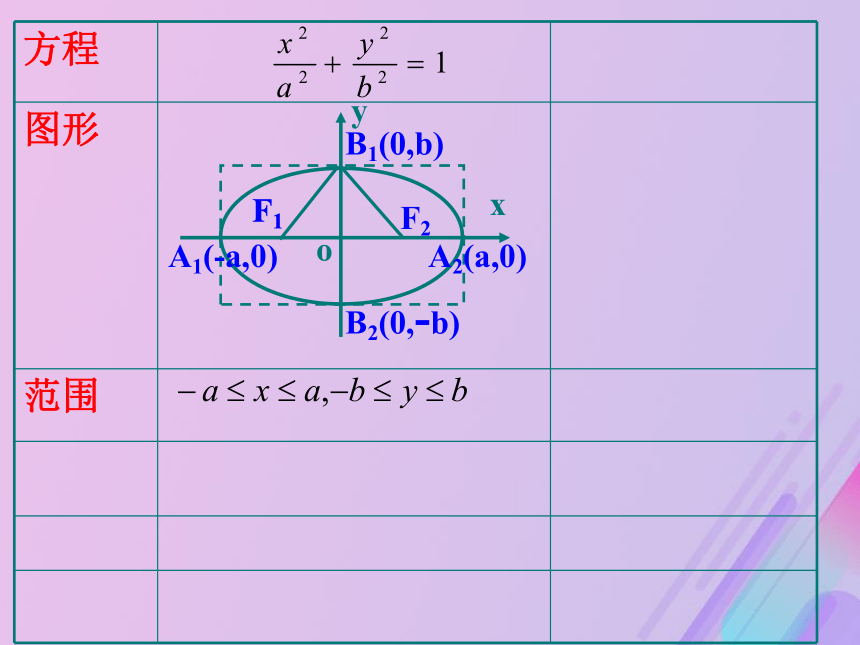
文档简介
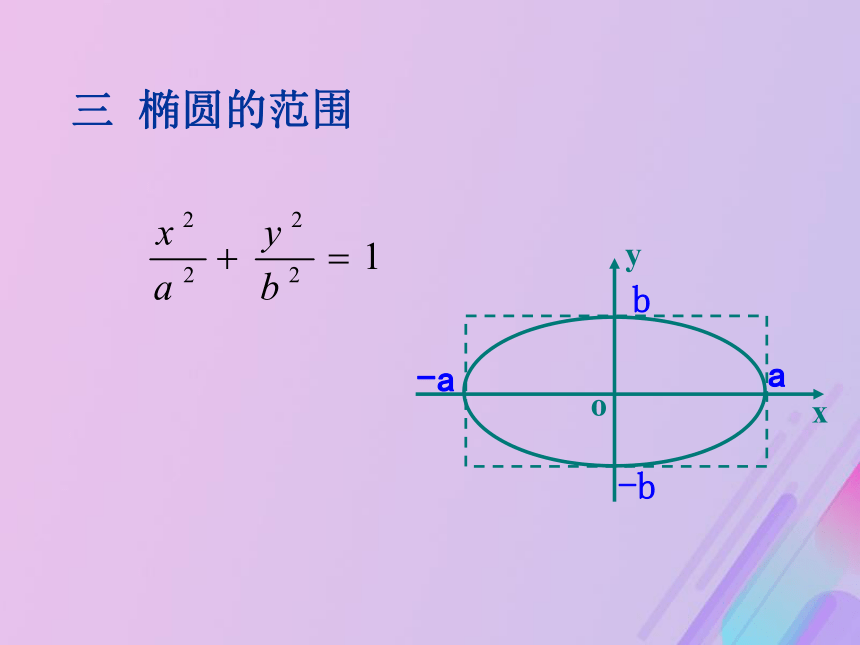
课件17张PPT。椭圆的几何性质(1)问题导入:1.椭圆的标准方程是什么?3.我们研究曲线的性质,通常研究曲线的哪写内容? 2.椭圆中a,b,c的关系? 以焦点在X轴椭圆的图形研究椭圆的性质b-ba-a方程:3、对称性:一 椭圆的对称性 oxy从图形上看:椭圆关于x轴、y轴、原点对称。从方程上看:(3)把x换成-x,同时把y换成-y方程不变,图象关于原点成中心对称。(2)把y换成-y方程不变,图象关于x轴对称;(1)把x换成-x方程不变,图象关于y轴对称;二 椭圆的顶点在中,令 x=0,得 y=?,说明椭圆与 y轴的交( , ),
令 y=0,得 x=?,说明椭圆与 x轴的交点( , )*顶点:椭圆与它的对称交点,叫做椭圆的顶点。
*长轴、短轴:段A1A2、B1B2分别叫做椭圆的长轴和短轴。
a、b分别叫做椭圆的长半轴长和短半轴长。 oxyB1(0,b)B2(0,-b)A1(-a,0)A2(a,0)︱ ︱
F1 F2
0 ±b±a 0 三 椭圆的范围b-ba-a关于x轴,y轴,原点对称。
关于x轴,y轴,原点对称。关于x轴,y轴,原点
对称。说出下列椭圆的长半轴长,短半轴长,顶点,对称性,并画出草图.xyo讨论:当长轴长不变时,
b变大,椭圆有什么样的变化?为什么?
四、椭圆的离心率1、离心率的取值范围:
因为 a > c > 0,所以1 >e >02、离心率对椭圆形状的影响:(2)e 越接近 0,c 就越接近 0,从而 b就越_____,椭圆就越_______.(1)e 越接近 1,c 就越接近 a,从而 b就越_____,椭圆就越_______.关于x轴,y轴,原点对称。关于x轴,y轴,原点
对称。练习求椭圆16x2+25y2=400的长轴和短轴长,离心率,焦点和顶点坐标解:把已知方程化为标准方程椭圆的四个顶点是A1(-5,0)、A2(5,0)、
B1(0,-4)、B2(0,4) 离心率焦点F1(-3,0)和F2(3,0),因此长轴长 ,短轴长 例2.利用椭圆的性质求椭圆的标准方程:
(1)经过点P(-3,0),Q(0,-2);
(2)长轴长等于20,离心率等于 .解:(1)由椭圆的几何性质可知,点P、Q分别为椭圆为所求椭圆的标准方程 .长轴和短轴的一个端点.
布置作业(一)?1.P103习题8.2 3、4?
(二)1.预习内容:P100-101例3,例4?
2.预习提纲:?
(1)椭圆的第二定义是什么?
?
(2)椭圆的准线是怎样定义的?
?
(3)对于一个确定的椭圆,它有几条准线?
?
(4)中心在原点,焦点在y轴上的椭圆,它的准线方程
是怎样的??再见
令 y=0,得 x=?,说明椭圆与 x轴的交点( , )*顶点:椭圆与它的对称交点,叫做椭圆的顶点。
*长轴、短轴:段A1A2、B1B2分别叫做椭圆的长轴和短轴。
a、b分别叫做椭圆的长半轴长和短半轴长。 oxyB1(0,b)B2(0,-b)A1(-a,0)A2(a,0)︱ ︱
F1 F2
0 ±b±a 0 三 椭圆的范围b-ba-a关于x轴,y轴,原点对称。
关于x轴,y轴,原点对称。关于x轴,y轴,原点
对称。说出下列椭圆的长半轴长,短半轴长,顶点,对称性,并画出草图.xyo讨论:当长轴长不变时,
b变大,椭圆有什么样的变化?为什么?
四、椭圆的离心率1、离心率的取值范围:
因为 a > c > 0,所以1 >e >02、离心率对椭圆形状的影响:(2)e 越接近 0,c 就越接近 0,从而 b就越_____,椭圆就越_______.(1)e 越接近 1,c 就越接近 a,从而 b就越_____,椭圆就越_______.关于x轴,y轴,原点对称。关于x轴,y轴,原点
对称。练习求椭圆16x2+25y2=400的长轴和短轴长,离心率,焦点和顶点坐标解:把已知方程化为标准方程椭圆的四个顶点是A1(-5,0)、A2(5,0)、
B1(0,-4)、B2(0,4) 离心率焦点F1(-3,0)和F2(3,0),因此长轴长 ,短轴长 例2.利用椭圆的性质求椭圆的标准方程:
(1)经过点P(-3,0),Q(0,-2);
(2)长轴长等于20,离心率等于 .解:(1)由椭圆的几何性质可知,点P、Q分别为椭圆为所求椭圆的标准方程 .长轴和短轴的一个端点.
布置作业(一)?1.P103习题8.2 3、4?
(二)1.预习内容:P100-101例3,例4?
2.预习提纲:?
(1)椭圆的第二定义是什么?
?
(2)椭圆的准线是怎样定义的?
?
(3)对于一个确定的椭圆,它有几条准线?
?
(4)中心在原点,焦点在y轴上的椭圆,它的准线方程
是怎样的??再见
