2018年高中数学新人教B版选修1-1课件:第三章导数及其应用3.1.3导数的几何意义课件(16张)
文档属性
| 名称 | 2018年高中数学新人教B版选修1-1课件:第三章导数及其应用3.1.3导数的几何意义课件(16张) |

|
|
| 格式 | zip | ||
| 文件大小 | 761.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-21 00:00:00 | ||
图片预览



文档简介
课件16张PPT。选修1-1
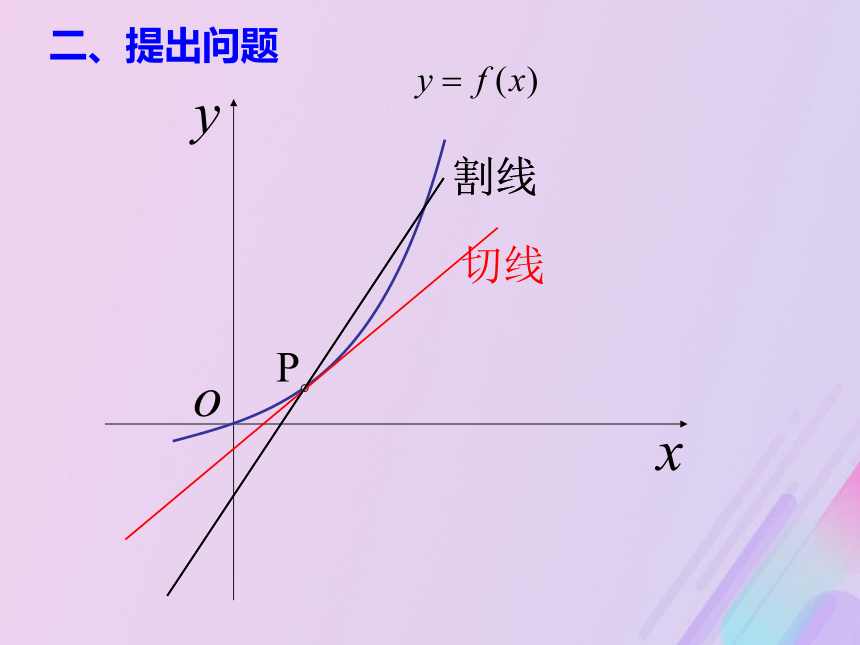
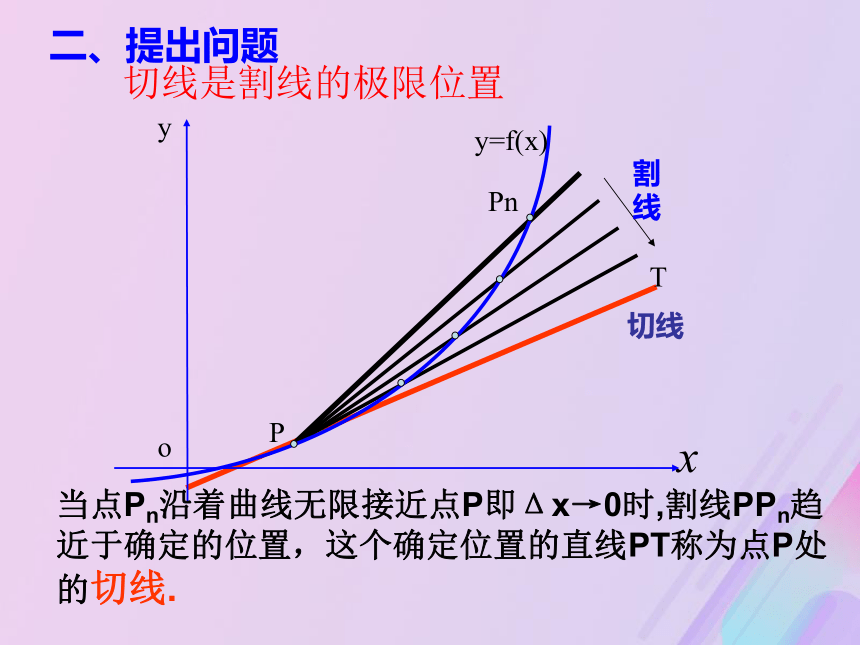
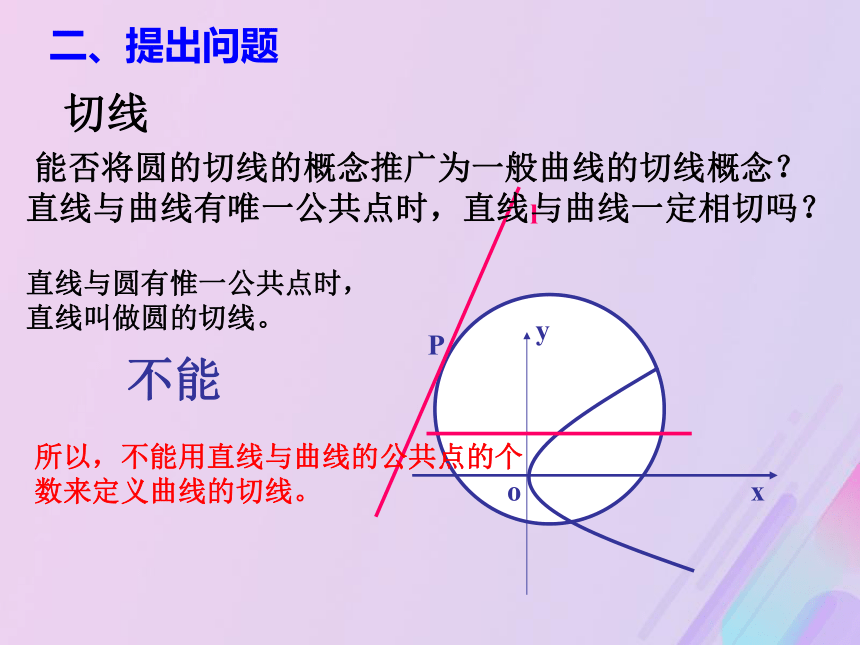
3.1.3导数的几何意义?一、复习引入P割线割线的斜率P切线割线二、提出问题割线PPn割线切线T当点Pn沿着曲线无限接近点P即Δx→0时,割线PPn趋近于确定的位置,这个确定位置的直线PT称为点P处的切线.切线是割线的极限位置二、提出问题切线 能否将圆的切线的概念推广为一般曲线的切线概念?直线与曲线有唯一公共点时,直线与曲线一定相切吗?不能直线与圆有惟一公共点时,
直线叫做圆的切线。所以,不能用直线与曲线的公共点的个数来定义曲线的切线。二、提出问题
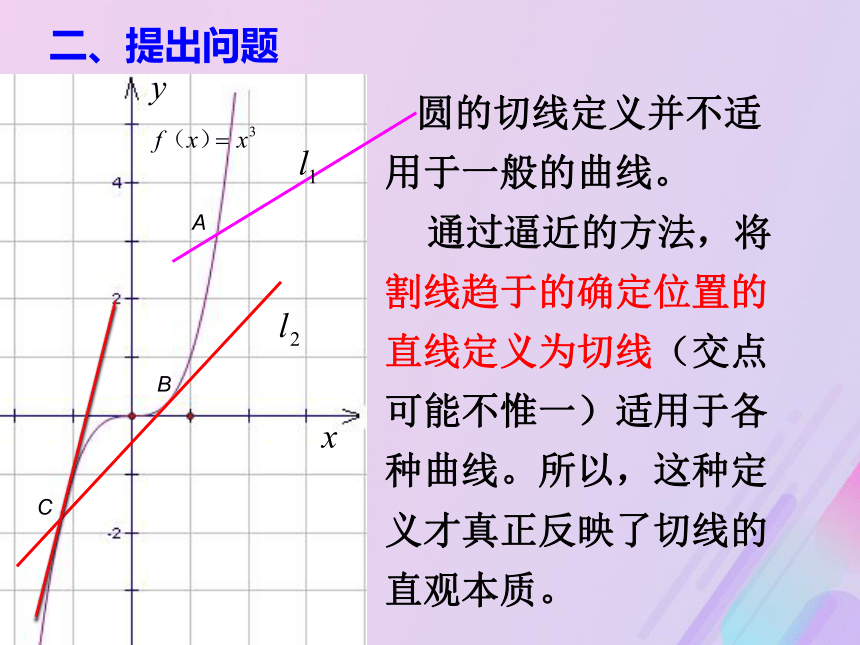
圆的切线定义并不适用于一般的曲线。
通过逼近的方法,将割线趋于的确定位置的直线定义为切线(交点可能不惟一)适用于各种曲线。所以,这种定义才真正反映了切线的直观本质。
二、提出问题ABC 函数 y=f(x)在点x0处的导数故曲线y=f(x)在点P(x0 ,f(x0))处的切线方程是:几何意义三、概念形成曲线y=f(x)在点P(x0 ,f(x0)) 处的切线的斜率四、应用举例四、应用举例变式1.求曲线C的切线中斜率最小的切线方程。变式2.曲线C过点P的切线有几条?四、应用举例 利用导数的几何意义求切线方程
(1)若已知点(x0,y0)是切点,则先求出函数y=f(x)在点x0处的导数f′(x0)即为切线斜率,然后切线方程
四、应用举例(2)若已知点(x0,y0)不是切点,首先应设出切点坐标,然后根据导数的几何意义列出等式,求出切点坐标,进而求出切线方程四、应用举例1.下面函数在x=0处的导数是否存在?结论:可导函数的图像是连续光滑的曲线五、思考在x=0处的切线是否存在?
如果存在求出切线方程。 函数 y=f(x)在点x0处的导数故曲线y=f(x)在点P(x0 ,f(x0))处的切线方程是:几何意义曲线y=f(x)在点P(x0 ,f(x0)) 处的切线的斜率练习:如图,已知曲线 ,求:
(1)点P处的切线的斜率; (2)点P处的切线方程.即点P处的切线的斜率等于4. (2)在点P处的切线方程是y-8/3=4(x-2),即12x-3y-16=0.
3.1.3导数的几何意义?一、复习引入P割线割线的斜率P切线割线二、提出问题割线PPn割线切线T当点Pn沿着曲线无限接近点P即Δx→0时,割线PPn趋近于确定的位置,这个确定位置的直线PT称为点P处的切线.切线是割线的极限位置二、提出问题切线 能否将圆的切线的概念推广为一般曲线的切线概念?直线与曲线有唯一公共点时,直线与曲线一定相切吗?不能直线与圆有惟一公共点时,
直线叫做圆的切线。所以,不能用直线与曲线的公共点的个数来定义曲线的切线。二、提出问题
圆的切线定义并不适用于一般的曲线。
通过逼近的方法,将割线趋于的确定位置的直线定义为切线(交点可能不惟一)适用于各种曲线。所以,这种定义才真正反映了切线的直观本质。
二、提出问题ABC 函数 y=f(x)在点x0处的导数故曲线y=f(x)在点P(x0 ,f(x0))处的切线方程是:几何意义三、概念形成曲线y=f(x)在点P(x0 ,f(x0)) 处的切线的斜率四、应用举例四、应用举例变式1.求曲线C的切线中斜率最小的切线方程。变式2.曲线C过点P的切线有几条?四、应用举例 利用导数的几何意义求切线方程
(1)若已知点(x0,y0)是切点,则先求出函数y=f(x)在点x0处的导数f′(x0)即为切线斜率,然后切线方程
四、应用举例(2)若已知点(x0,y0)不是切点,首先应设出切点坐标,然后根据导数的几何意义列出等式,求出切点坐标,进而求出切线方程四、应用举例1.下面函数在x=0处的导数是否存在?结论:可导函数的图像是连续光滑的曲线五、思考在x=0处的切线是否存在?
如果存在求出切线方程。 函数 y=f(x)在点x0处的导数故曲线y=f(x)在点P(x0 ,f(x0))处的切线方程是:几何意义曲线y=f(x)在点P(x0 ,f(x0)) 处的切线的斜率练习:如图,已知曲线 ,求:
(1)点P处的切线的斜率; (2)点P处的切线方程.即点P处的切线的斜率等于4. (2)在点P处的切线方程是y-8/3=4(x-2),即12x-3y-16=0.
