2018年高中数学新人教B版选修1-1课件:第二章圆锥曲线与方程2.1.1椭圆及其标准方程课件(20张)
文档属性
| 名称 | 2018年高中数学新人教B版选修1-1课件:第二章圆锥曲线与方程2.1.1椭圆及其标准方程课件(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 663.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-22 08:25:19 | ||
图片预览








文档简介
课件20张PPT。椭圆及其标准方程导入新课请你们利用细绳画一个圆?
请从集合的角度叙述圆的定义。
知识衔接平面上到定点的距离等于定长的点的集合叫圆.活动探究思考:怎样画椭圆?观察这条曲线上所有的点满足什么条件?
如何用集合描述这个条件?
探究一:椭圆的定义椭圆的定义:
平面上与两个定点F1,F2距离之和是常数
的点的轨迹叫做椭圆。
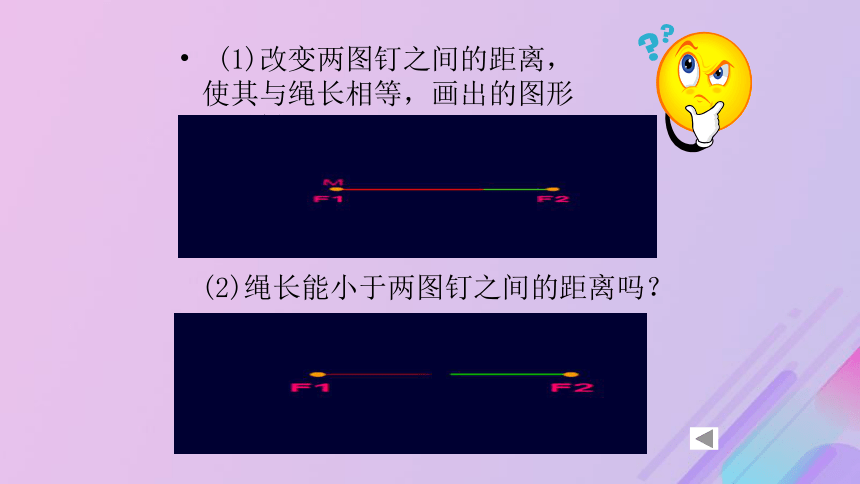
(大于| F1F2 |)焦点2a焦距 2c (1)改变两图钉之间的距离,使其与绳长相等,画出的图形还是椭圆吗?(2)绳长能小于两图钉之间的距离吗? 1)建立直角坐标系:
2)设动点M的坐标
3)列等式
4)化简方程
微课探究二:椭圆的标准方程思考:若焦点在y轴上,标准方程是什么? Y?椭圆的标准方程的特点:(2)形式:左边是两个分式的平方和,右边是1。(1)三个参数a、b、c的关系: 。(3)焦点所在位置: 的分母哪个大,则焦点在哪个轴上。实战演练例1、已知椭圆的焦点在x轴上,焦距是6,椭圆上一点到两个焦点的距离之和是10,写出这个椭圆的标准方程。解:因为2c=6,2a=10,所以 c=3,a=5,从而
由于焦点在x轴上,因此这个椭圆的标准方程是定义法例2:已知椭圆的焦点在x轴上,焦距为2,且椭圆经过点P(2,0)求椭圆的标准方程。解:因为椭圆的焦点在x轴上,
所以设椭圆的标准方程是又因为焦距是2,所以2c=2,即c=1
所以 因为椭圆经过点P(2,0)
所以故椭圆的标准方程为待定系数法即例3:求椭圆 的焦点和焦距。解:由于所以由题可知,焦点在x轴上,椭圆解题关键:
1、判断焦点所在位置
2、寻找a ,b ,c的值焦距为12因此焦点为答:在 x 轴上,(-3,0)和(3,0)答:在 y 轴上,(0,-5)和(0,5)1.判定下列椭圆的焦点在 哪个轴上,写出焦点坐标。强化训练快速口答答:在y 轴上,(0,-1)和(0,1)焦点在分母大的那个轴上。答:在x轴上,(-3,0)和(3,0)
答:在y轴上,(0,-12)和(0,12)
快速口答3.两个焦点的坐标分别是(0,-2)、(0,2)
并且椭圆经过点(-3/2,5/2),求椭圆的方程。2.椭圆的两个焦点的坐标分别是(-4, 0 )、( 4 , 0 ),
椭圆上一点P到两焦点距离之和等于10 ,求椭圆的标准方程。 分组练习2、椭圆的两个焦点的坐标分别是(-4, 0 )、( 4 , 0 ),
,求椭圆的标准方程。 解: ∵椭圆的焦点在x轴上
且2a=10, 2c=8
∴ a=5, c=4
∴ b2=a2-c2=52-42=9
∴所求椭圆的标准方程为: 分组练习椭圆上一点P到两焦点距离之和等于103、两个焦点的坐标分别是(0,-2)、(0,2)
并且椭圆经过点(3/2,5/2),求椭圆的方程。解:已知焦点为(0,-2)(0,2).
可知焦点在y轴上,且C=2由椭圆的定义知:所以椭圆的方程为:分组练习4.分别求出各组所画椭圆的标准方程。5.帮木匠师傅设计椭圆造型。实际应用课堂小结二类方程:一个定义:椭圆的定义
求椭圆标准方程的方法两种方法:分母哪个大,焦点就在哪个轴上平面内到两个定点F1,F2的距离的和等
于常数(大于F1F2)的点的轨迹?再认识!
请从集合的角度叙述圆的定义。
知识衔接平面上到定点的距离等于定长的点的集合叫圆.活动探究思考:怎样画椭圆?观察这条曲线上所有的点满足什么条件?
如何用集合描述这个条件?
探究一:椭圆的定义椭圆的定义:
平面上与两个定点F1,F2距离之和是常数
的点的轨迹叫做椭圆。
(大于| F1F2 |)焦点2a焦距 2c (1)改变两图钉之间的距离,使其与绳长相等,画出的图形还是椭圆吗?(2)绳长能小于两图钉之间的距离吗? 1)建立直角坐标系:
2)设动点M的坐标
3)列等式
4)化简方程
微课探究二:椭圆的标准方程思考:若焦点在y轴上,标准方程是什么? Y?椭圆的标准方程的特点:(2)形式:左边是两个分式的平方和,右边是1。(1)三个参数a、b、c的关系: 。(3)焦点所在位置: 的分母哪个大,则焦点在哪个轴上。实战演练例1、已知椭圆的焦点在x轴上,焦距是6,椭圆上一点到两个焦点的距离之和是10,写出这个椭圆的标准方程。解:因为2c=6,2a=10,所以 c=3,a=5,从而
由于焦点在x轴上,因此这个椭圆的标准方程是定义法例2:已知椭圆的焦点在x轴上,焦距为2,且椭圆经过点P(2,0)求椭圆的标准方程。解:因为椭圆的焦点在x轴上,
所以设椭圆的标准方程是又因为焦距是2,所以2c=2,即c=1
所以 因为椭圆经过点P(2,0)
所以故椭圆的标准方程为待定系数法即例3:求椭圆 的焦点和焦距。解:由于所以由题可知,焦点在x轴上,椭圆解题关键:
1、判断焦点所在位置
2、寻找a ,b ,c的值焦距为12因此焦点为答:在 x 轴上,(-3,0)和(3,0)答:在 y 轴上,(0,-5)和(0,5)1.判定下列椭圆的焦点在 哪个轴上,写出焦点坐标。强化训练快速口答答:在y 轴上,(0,-1)和(0,1)焦点在分母大的那个轴上。答:在x轴上,(-3,0)和(3,0)
答:在y轴上,(0,-12)和(0,12)
快速口答3.两个焦点的坐标分别是(0,-2)、(0,2)
并且椭圆经过点(-3/2,5/2),求椭圆的方程。2.椭圆的两个焦点的坐标分别是(-4, 0 )、( 4 , 0 ),
椭圆上一点P到两焦点距离之和等于10 ,求椭圆的标准方程。 分组练习2、椭圆的两个焦点的坐标分别是(-4, 0 )、( 4 , 0 ),
,求椭圆的标准方程。 解: ∵椭圆的焦点在x轴上
且2a=10, 2c=8
∴ a=5, c=4
∴ b2=a2-c2=52-42=9
∴所求椭圆的标准方程为: 分组练习椭圆上一点P到两焦点距离之和等于103、两个焦点的坐标分别是(0,-2)、(0,2)
并且椭圆经过点(3/2,5/2),求椭圆的方程。解:已知焦点为(0,-2)(0,2).
可知焦点在y轴上,且C=2由椭圆的定义知:所以椭圆的方程为:分组练习4.分别求出各组所画椭圆的标准方程。5.帮木匠师傅设计椭圆造型。实际应用课堂小结二类方程:一个定义:椭圆的定义
求椭圆标准方程的方法两种方法:分母哪个大,焦点就在哪个轴上平面内到两个定点F1,F2的距离的和等
于常数(大于F1F2)的点的轨迹?再认识!
