2018年高中数学新人教B版选修1-1课件:第二章圆锥曲线与方程2.1.2椭圆的几何性质课件(19张)
文档属性
| 名称 | 2018年高中数学新人教B版选修1-1课件:第二章圆锥曲线与方程2.1.2椭圆的几何性质课件(19张) |  | |
| 格式 | zip | ||
| 文件大小 | 940.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-22 08:25:37 | ||
图片预览




文档简介
课件19张PPT。椭圆的几何性质复习:1.椭圆的定义:到两定点F1、F2的距离和为常数(大于|F1F2 |)的点的轨迹叫做椭圆。2.椭圆的标准方程是:3.椭圆中a,b,c的关系是:a2=b2+c21.若|MF1|+ |MF2|=2a(2a是常数)2.标准方程求椭圆标准方程的方法:
----------待定系数法.当2a>|F1F2|时,点M的轨迹是________;
当2a=|F1F2|时,点M的轨迹是________;
当2a<|F1F2|时,点M的轨迹是________.椭圆线段F1F2不存在求椭圆标准方程的步骤:
(1)确定焦点位置,设椭圆的标准方程
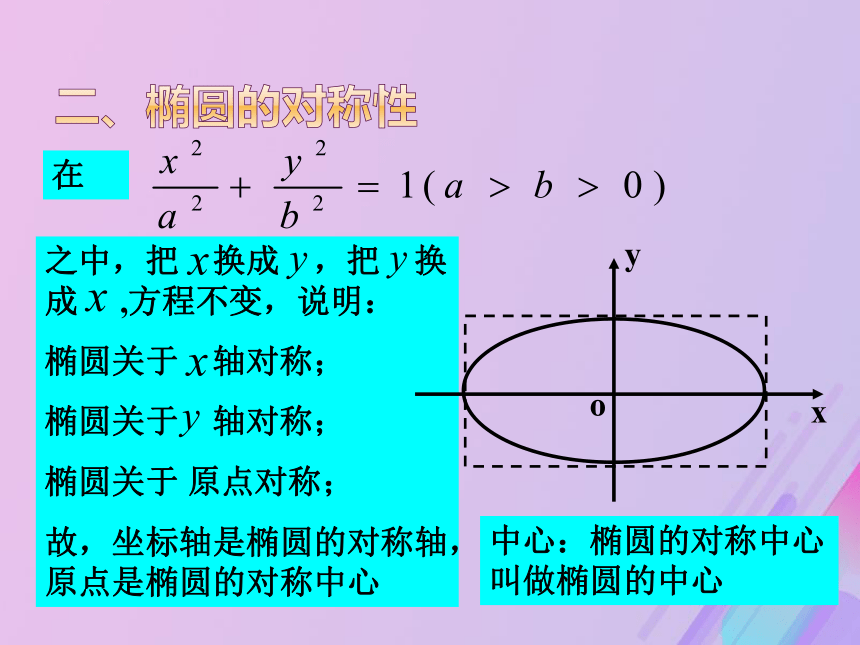
(2)求a,b(常建立方程 组)(3) 下结论一、椭圆的范围由说明:椭圆位于矩形之中。二、椭圆的对称性在之中,把 换成 ,把 换成 ,方程不变,说明:
椭圆关于 轴对称;
椭圆关于 轴对称;
椭圆关于 原点对称;
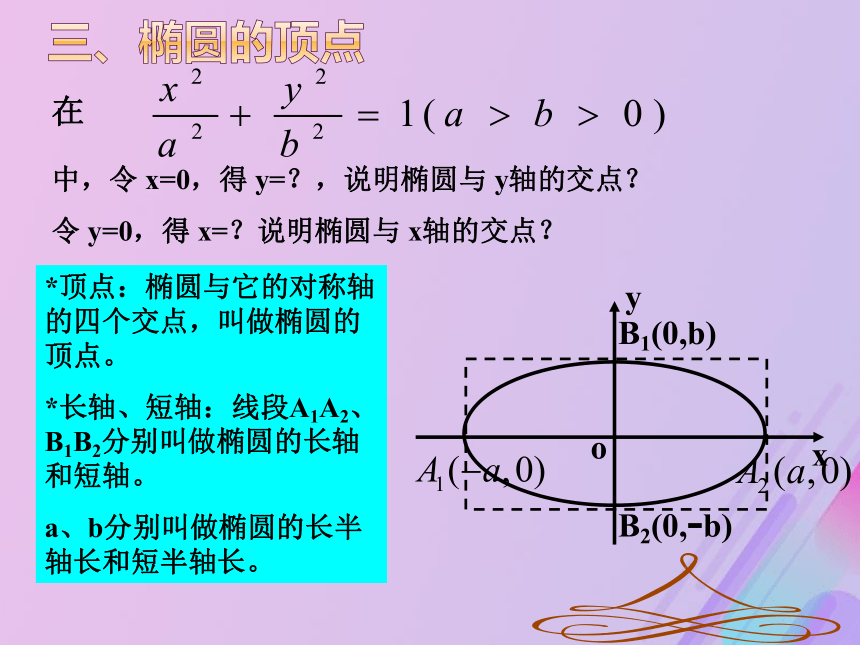
故,坐标轴是椭圆的对称轴,原点是椭圆的对称中心中心:椭圆的对称中心叫做椭圆的中心三、椭圆的顶点在中,令 x=0,得 y=?,说明椭圆与 y轴的交点?
令 y=0,得 x=?说明椭圆与 x轴的交点?*顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。
*长轴、短轴:线段A1A2、B1B2分别叫做椭圆的长轴和短轴。
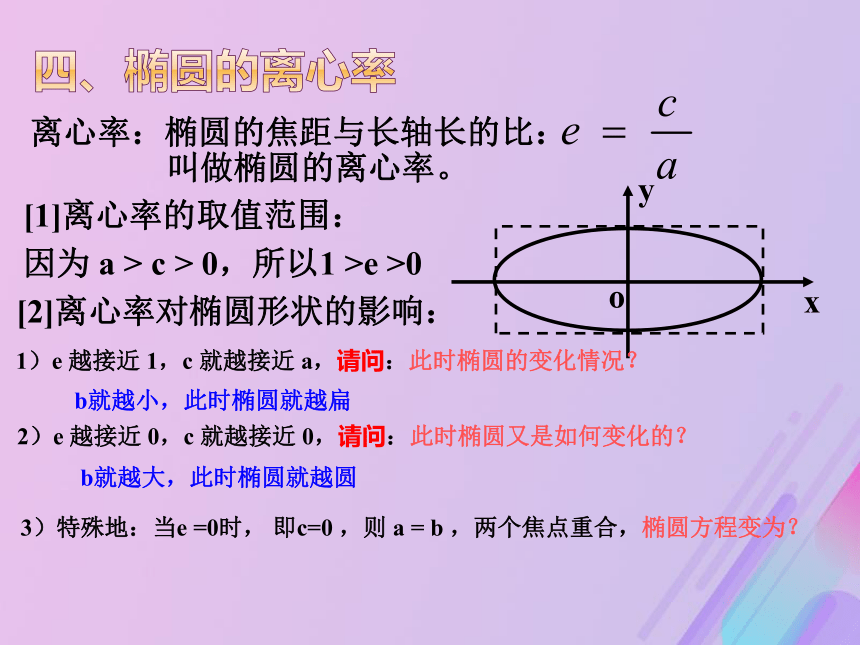
a、b分别叫做椭圆的长半轴长和短半轴长。四、椭圆的离心率离心率:椭圆的焦距与长轴长的比:叫做椭圆的离心率。[1]离心率的取值范围:
因为 a > c > 0,所以1 >e >0[2]离心率对椭圆形状的影响:
1)e 越接近 1,c 就越接近 a,请问:此时椭圆的变化情况?
b就越小,此时椭圆就越扁 2)e 越接近 0,c 就越接近 0,请问:此时椭圆又是如何变化的?b就越大,此时椭圆就越圆 3)特殊地:当e =0时, 即c=0 ,则 a = b ,两个焦点重合,椭圆方程变为?
|x|≤ a,|y|≤ b|x|≤ b,|y|≤ a关于x轴、y轴成轴对称;关于原点成中心对称。( a ,0 ),(0, b)( b ,0 ),(0, a)( c,0)(0, c)长半轴长为a,短半轴长为b.焦距为2c;a2=b2+c2例1已知椭圆方程为16x2+25y2=400, 它的长轴长是: 。短轴长是: 。
焦距是: 。 离心率等于: 。
焦点坐标是: 。顶点坐标是: 。 1086分析:椭圆方程转化为标准方程为:
练习(1) 若椭圆 的焦点在x轴上,离心率 ,则m= 。 若椭圆的长轴长不大于短轴长的2倍,则椭圆的离心率 。作业1.已知椭圆方程为6x2+y2=6它的长轴长是: 。短轴长是: 。
焦距是: 。 离心率等于: 。
焦点坐标是: 。顶点坐标是: 。 2.已知椭圆中心在原点,对称轴为坐标轴,焦点在y轴,长轴是短轴的2倍,焦距为2,离心率为 ,求椭圆的方程。
----------待定系数法.当2a>|F1F2|时,点M的轨迹是________;
当2a=|F1F2|时,点M的轨迹是________;
当2a<|F1F2|时,点M的轨迹是________.椭圆线段F1F2不存在求椭圆标准方程的步骤:
(1)确定焦点位置,设椭圆的标准方程
(2)求a,b(常建立方程 组)(3) 下结论一、椭圆的范围由说明:椭圆位于矩形之中。二、椭圆的对称性在之中,把 换成 ,把 换成 ,方程不变,说明:
椭圆关于 轴对称;
椭圆关于 轴对称;
椭圆关于 原点对称;
故,坐标轴是椭圆的对称轴,原点是椭圆的对称中心中心:椭圆的对称中心叫做椭圆的中心三、椭圆的顶点在中,令 x=0,得 y=?,说明椭圆与 y轴的交点?
令 y=0,得 x=?说明椭圆与 x轴的交点?*顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。
*长轴、短轴:线段A1A2、B1B2分别叫做椭圆的长轴和短轴。
a、b分别叫做椭圆的长半轴长和短半轴长。四、椭圆的离心率离心率:椭圆的焦距与长轴长的比:叫做椭圆的离心率。[1]离心率的取值范围:
因为 a > c > 0,所以1 >e >0[2]离心率对椭圆形状的影响:
1)e 越接近 1,c 就越接近 a,请问:此时椭圆的变化情况?
b就越小,此时椭圆就越扁 2)e 越接近 0,c 就越接近 0,请问:此时椭圆又是如何变化的?b就越大,此时椭圆就越圆 3)特殊地:当e =0时, 即c=0 ,则 a = b ,两个焦点重合,椭圆方程变为?
|x|≤ a,|y|≤ b|x|≤ b,|y|≤ a关于x轴、y轴成轴对称;关于原点成中心对称。( a ,0 ),(0, b)( b ,0 ),(0, a)( c,0)(0, c)长半轴长为a,短半轴长为b.焦距为2c;a2=b2+c2例1已知椭圆方程为16x2+25y2=400, 它的长轴长是: 。短轴长是: 。
焦距是: 。 离心率等于: 。
焦点坐标是: 。顶点坐标是: 。 1086分析:椭圆方程转化为标准方程为:
练习(1) 若椭圆 的焦点在x轴上,离心率 ,则m= 。 若椭圆的长轴长不大于短轴长的2倍,则椭圆的离心率 。作业1.已知椭圆方程为6x2+y2=6它的长轴长是: 。短轴长是: 。
焦距是: 。 离心率等于: 。
焦点坐标是: 。顶点坐标是: 。 2.已知椭圆中心在原点,对称轴为坐标轴,焦点在y轴,长轴是短轴的2倍,焦距为2,离心率为 ,求椭圆的方程。
