2018年高中数学新人教B版选修1-1课件:第二章圆锥曲线与方程2.2.2双曲线的几何性质课件(17张)
文档属性
| 名称 | 2018年高中数学新人教B版选修1-1课件:第二章圆锥曲线与方程2.2.2双曲线的几何性质课件(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 366.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-22 08:26:15 | ||
图片预览






文档简介
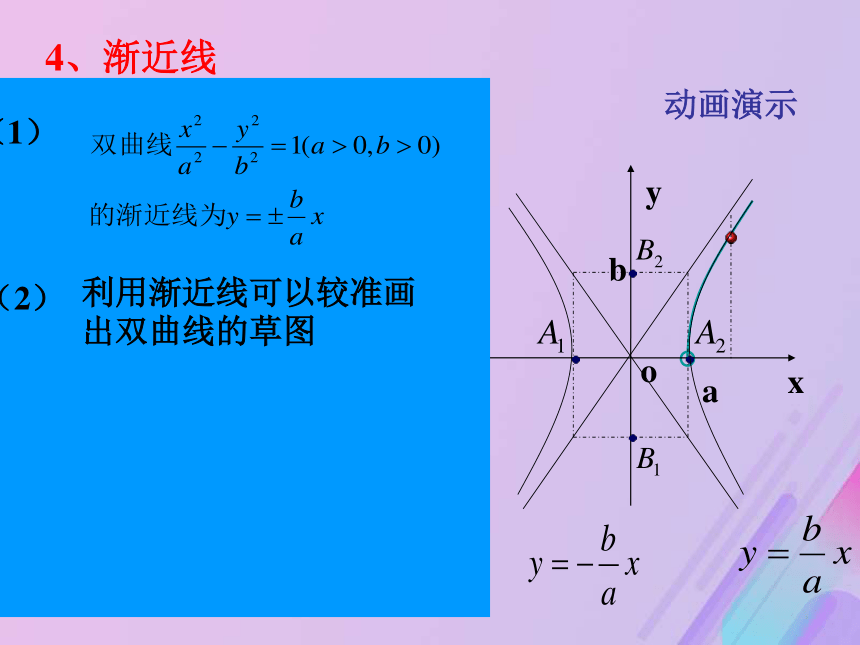
课件17张PPT。 双曲线的几何性质| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)F ( ±c, 0) F(0, ± c) 2、对称性 一、研究双曲线 的简单几何性质1、范围关于x轴、y轴和原点都是对称。x轴、y轴是双曲线的对称轴,原点是对称中心,
又叫做双曲线的中心。(-x,-y)(-x,y)(x,y)(x,-y)课堂新授 3、顶点(1)双曲线与对称轴的交点,叫做双曲线的顶点4、渐近线动画演示5、离心率离心率。c>a>0e >1e是表示双曲线开口大小的一个量,e越大开口越大(1)定义 :(2)e的范围:(3)e的含义:(4)等轴双曲线的离心率e= ?( 5 )(1)范围:(4)渐近线:(5)离心率:例1 求双曲线 16x2-9y2=144的实半轴长和虚半轴长、焦点坐标、离心率、渐进线方程.9例2 练习
1、2、 的渐近线方程为:_______ 的实轴长 虚轴长为_____ 顶点坐标为 ,焦点坐标为_________
离心率为_______4的渐近线方程为: 的渐近线方程为: 的渐近线方程为: 1112高考链接1.已知(2,0)是双曲线 的一个焦点,则 b=___
2.双曲线 的焦距是 ___ ,渐近线方程是___
3.已知双曲线 的一条渐近线为 ,则a=___13小 结或或关于坐标
轴和
原点
都对
称14练习:求出下列双曲线的标准方程15DA1617
又叫做双曲线的中心。(-x,-y)(-x,y)(x,y)(x,-y)课堂新授 3、顶点(1)双曲线与对称轴的交点,叫做双曲线的顶点4、渐近线动画演示5、离心率离心率。c>a>0e >1e是表示双曲线开口大小的一个量,e越大开口越大(1)定义 :(2)e的范围:(3)e的含义:(4)等轴双曲线的离心率e= ?( 5 )(1)范围:(4)渐近线:(5)离心率:例1 求双曲线 16x2-9y2=144的实半轴长和虚半轴长、焦点坐标、离心率、渐进线方程.9例2 练习
1、2、 的渐近线方程为:_______ 的实轴长 虚轴长为_____ 顶点坐标为 ,焦点坐标为_________
离心率为_______4的渐近线方程为: 的渐近线方程为: 的渐近线方程为: 1112高考链接1.已知(2,0)是双曲线 的一个焦点,则 b=___
2.双曲线 的焦距是 ___ ,渐近线方程是___
3.已知双曲线 的一条渐近线为 ,则a=___13小 结或或关于坐标
轴和
原点
都对
称14练习:求出下列双曲线的标准方程15DA1617
