2018年高中数学新人教B版选修1-1课件:第二章圆锥曲线与方程2.3.1抛物线级其标准方程课件(16张)
文档属性
| 名称 | 2018年高中数学新人教B版选修1-1课件:第二章圆锥曲线与方程2.3.1抛物线级其标准方程课件(16张) |

|
|
| 格式 | zip | ||
| 文件大小 | 369.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-22 00:00:00 | ||
图片预览





文档简介
课件16张PPT。2.3.1 抛物线及其标准方程(一)学习目标掌握抛物线的定义及焦点、准线的概念.
掌握抛物线的标准方程及其推导.
明确抛物线标准方程中p的几何意义,能解决简单的求抛物线标准方程问题.复习回顾(1)、建系设点;(2)、列方程;
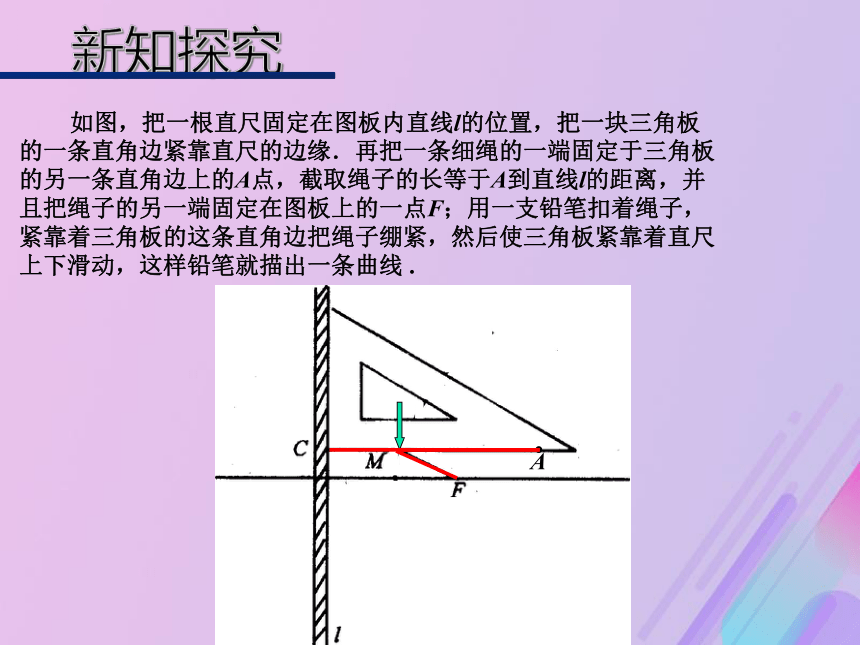
(3)、化简方程;(4)、检验完备性(可省略)对称性、单调性、顶点(最值)等1、椭圆和双曲线的定义分别是什么?对于椭圆、双曲线标准方程的求法包含了哪些步骤?2、对于初中所学抛物线它的解析式是______________,你能说出它有哪些性质吗? 如图,把一根直尺固定在图板内直线l的位置,把一块三角板
的一条直角边紧靠直尺的边缘.再把一条细绳的一端固定于三角板
的另一条直角边上的A点,截取绳子的长等于A到直线l的距离,并
且把绳子的另一端固定在图板上的一点F;用一支铅笔扣着绳子,
紧靠着三角板的这条直角边把绳子绷紧,然后使三角板紧靠着直尺
上下滑动,这样铅笔就描出一条曲线 .
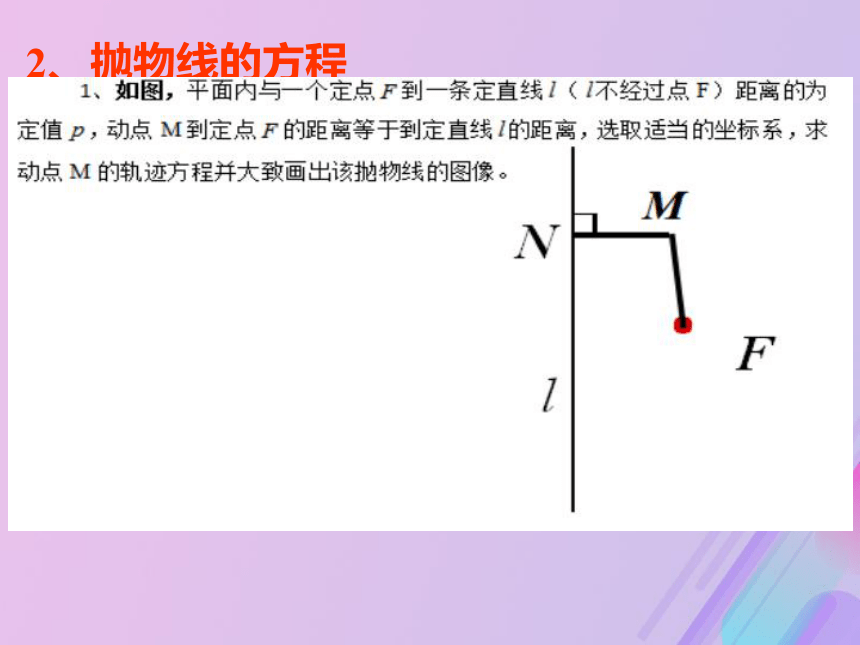
A 新知探究平面内与一个定点F和一条定直线 l(F不在l上)的距离相等的点的轨迹叫做抛物线.1、定义即:则点M的轨迹是抛物线 .定点F 叫做抛物线的焦点.
定直线l 叫做抛物线的准线. 想一想:若定点F在直线 上时,其它条件不变,动点M的轨迹是什么?2、抛物线的方程设︱KF︱= p (p>0),点 M(x,y), 由定义,|MF|=|MN|如图,建立直角坐标系:NN(1)(2)(3)标准方程 方程 y2 = 2px(p>0)叫做
抛物线的标准方程。其中p为正常数,它的几何意义是:它表示的抛物线的焦点在 x 轴的正半轴上,
坐标是 ,它的准线方程是 焦点到准线的距离但是,一条抛物线,由于它在坐标平面
内的位置不同,方程也不同,所以抛物
线的标准方程还有其它形式。3、抛物线的标准方程四种抛物线的标准方程: 例1. (1)已知抛物线的标准方程是 y2 = 6x,
求它的焦点坐标和准线方程;(2)已知抛物线的焦点坐标是F(0,-2),
求它的标准方程。(3)已知抛物线的方程是 y= 6x2,
求它的焦点坐标和准线方程. 例1. (1)已知抛物线的标准方程是 y2 = 6x,
求它的焦点坐标和准线方程;(2)已知抛物线的焦点坐标是F(0,-2),
求它的标准方程。解:(3)已知抛物线的方程是 y= 6x2,
求它的焦点坐标和准线方程.解:解:如图,在接收天线的轴截面所在平面内建立直角坐标系,使接收天线的顶点(即抛物线的顶点)与原点重合。设抛物线的标准方程是 由已知条件可得,点A的坐标是(0.5,2.4), 代入方程,得: 即所以,所求抛物线的标准方程是 ,焦点坐标是(2.88,0)解:设点C的坐标为由抛物线的定义可知:FC的长度等于C点到准线的距离,即由例2知: ,故而所以点C的坐标为课后思考抛物线 的焦点坐标和准线方程分别是多少?本堂小结 1、我们可以从哪些角度去判断一种曲线(轨迹)是否是抛物线?定义、方程2、求抛物线标准方程有哪些办法?直接法 定义法 待定系数法3、抛物线与椭圆、双曲线有哪些联系与区别?课后作业:教材73页 习题2.4 1、2、3、4 ;
练习册对应的活页
掌握抛物线的标准方程及其推导.
明确抛物线标准方程中p的几何意义,能解决简单的求抛物线标准方程问题.复习回顾(1)、建系设点;(2)、列方程;
(3)、化简方程;(4)、检验完备性(可省略)对称性、单调性、顶点(最值)等1、椭圆和双曲线的定义分别是什么?对于椭圆、双曲线标准方程的求法包含了哪些步骤?2、对于初中所学抛物线它的解析式是______________,你能说出它有哪些性质吗? 如图,把一根直尺固定在图板内直线l的位置,把一块三角板
的一条直角边紧靠直尺的边缘.再把一条细绳的一端固定于三角板
的另一条直角边上的A点,截取绳子的长等于A到直线l的距离,并
且把绳子的另一端固定在图板上的一点F;用一支铅笔扣着绳子,
紧靠着三角板的这条直角边把绳子绷紧,然后使三角板紧靠着直尺
上下滑动,这样铅笔就描出一条曲线 .
A 新知探究平面内与一个定点F和一条定直线 l(F不在l上)的距离相等的点的轨迹叫做抛物线.1、定义即:则点M的轨迹是抛物线 .定点F 叫做抛物线的焦点.
定直线l 叫做抛物线的准线. 想一想:若定点F在直线 上时,其它条件不变,动点M的轨迹是什么?2、抛物线的方程设︱KF︱= p (p>0),点 M(x,y), 由定义,|MF|=|MN|如图,建立直角坐标系:NN(1)(2)(3)标准方程 方程 y2 = 2px(p>0)叫做
抛物线的标准方程。其中p为正常数,它的几何意义是:它表示的抛物线的焦点在 x 轴的正半轴上,
坐标是 ,它的准线方程是 焦点到准线的距离但是,一条抛物线,由于它在坐标平面
内的位置不同,方程也不同,所以抛物
线的标准方程还有其它形式。3、抛物线的标准方程四种抛物线的标准方程: 例1. (1)已知抛物线的标准方程是 y2 = 6x,
求它的焦点坐标和准线方程;(2)已知抛物线的焦点坐标是F(0,-2),
求它的标准方程。(3)已知抛物线的方程是 y= 6x2,
求它的焦点坐标和准线方程. 例1. (1)已知抛物线的标准方程是 y2 = 6x,
求它的焦点坐标和准线方程;(2)已知抛物线的焦点坐标是F(0,-2),
求它的标准方程。解:(3)已知抛物线的方程是 y= 6x2,
求它的焦点坐标和准线方程.解:解:如图,在接收天线的轴截面所在平面内建立直角坐标系,使接收天线的顶点(即抛物线的顶点)与原点重合。设抛物线的标准方程是 由已知条件可得,点A的坐标是(0.5,2.4), 代入方程,得: 即所以,所求抛物线的标准方程是 ,焦点坐标是(2.88,0)解:设点C的坐标为由抛物线的定义可知:FC的长度等于C点到准线的距离,即由例2知: ,故而所以点C的坐标为课后思考抛物线 的焦点坐标和准线方程分别是多少?本堂小结 1、我们可以从哪些角度去判断一种曲线(轨迹)是否是抛物线?定义、方程2、求抛物线标准方程有哪些办法?直接法 定义法 待定系数法3、抛物线与椭圆、双曲线有哪些联系与区别?课后作业:教材73页 习题2.4 1、2、3、4 ;
练习册对应的活页
