2018年高中数学新人教B版选修1-1课件:第三章导数及其应用3.1.3导数的几何意义课件(19张)
文档属性
| 名称 | 2018年高中数学新人教B版选修1-1课件:第三章导数及其应用3.1.3导数的几何意义课件(19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-22 00:00:00 | ||
图片预览





文档简介
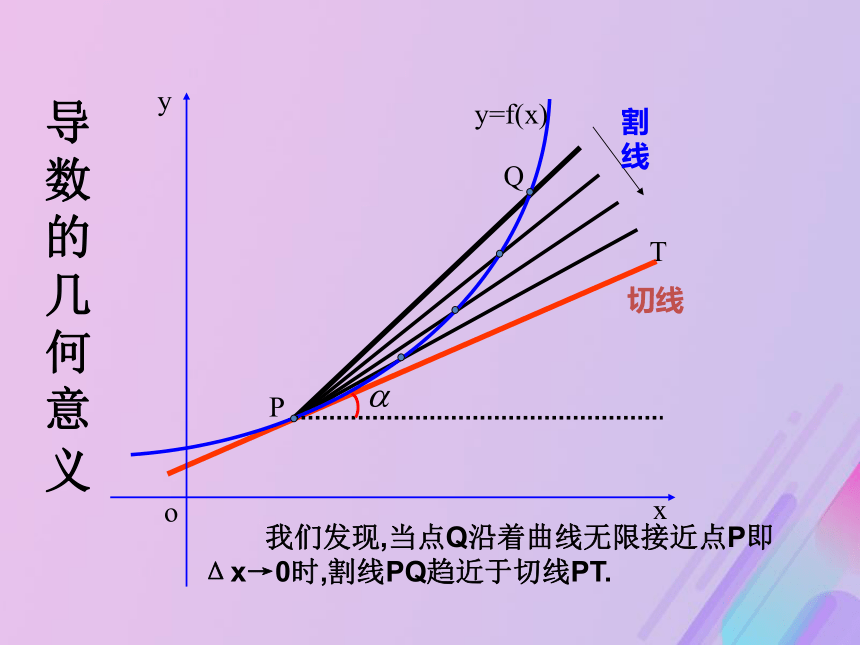
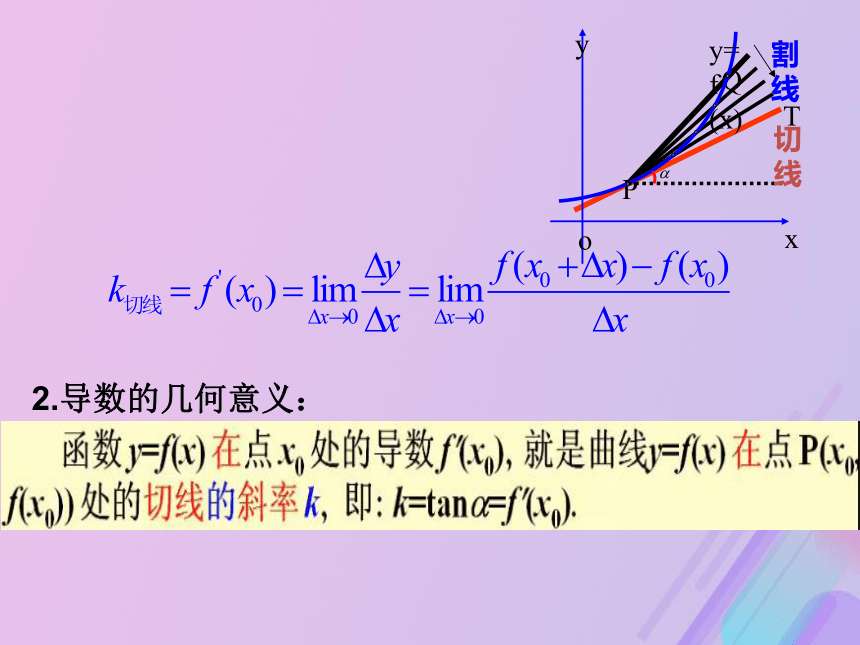
课件19张PPT。割线斜率2.导数的几何意义是什么呢?PQ切线T导数的几何意义 我们发现,当点Q沿着曲线无限接近点P即Δx→0时,割线PQ趋近于切线PT.2.导数的几何意义:
例一:
(1)求曲线y=x2+x+1在点x=1处的切点、导数、 斜率、 切线方程 解:把x=1带入y= x2+x+1 中得y=3故切点为(1,3) ∵y′=2x+1, ∴所求切线方程为y-3=3(x-1)即3x-y=0 思考:求切线的步骤?∴切线斜率k=3∴导数y′|x=1=2×1+1=31.求切点
2.利用求导公式求导数
3.求斜率
4.利用点斜式求切线方程求切线的步骤:练一:
(1)求曲线y=x2+x在点x=1处的切点、导数、 斜率、切线方程
(2)求曲线y=2x3在点(1,2)处的切线方程.
(3)求曲线y=x2 在点(1,1)处的切线方程. 解:(1)把x=1带入y= x2+x 中得y=2故切点为(1,2) ∵y′=2x+1 ∴所求切线方程为y-2=3(x-1)即y-3x+1=0 ∴切线斜率k=3∴导数y′|x=1=2×1+1=3 (2)求曲线y=2x3在点(1,2)处的切线方程.解: ∵(1,2)在曲线上y′=6x2∴切线斜率k=y′|x=1=6×1=6∴所求切线方程为y-2=6(x-1)即y-6x+4=0(3)求曲线y=x2 在点(1,1)处的切线方程.
解:(1) ∵(1,1)在曲线上,y′=2x
∴切线斜率k=y′|x=1=2×1=2
∴所求切线方程为y-1=2(x-1),
即y-2x+1=0例二:
(1)抛物线y=x2在点P处的切线与直线4x-y+2=0
平行,求P点的坐标及切线方程.解: 设切点P点坐标为(x0,y0) ∵ y′=2x. ∴y′|x=x0=2x0又由切线与直线4x-y+2=0平行∴2x0=4,∴x0=2∵P(2,y0)在抛物线y=x2上∴y0=4∴点P的坐标为(2,4)∴切线方程为y-4=4(x-2)即4x-y-4=0(2)抛物线y=x2在点P处的切线与直线4x-y+2=0垂直,求P点的坐标.解: 设切点P点坐标为(x0,y0),
∵ y′=2x. ∴y′|x=x0=2x0,
又由切线与直线4x-y+2=0垂直,
∴4×2x0 =-1,∴x0=-
∵P(- ,y0)在抛物线y=x2上,
∴y0=
∴点P的坐标为(- , ),
练习二:在曲线y=x2上过哪一点的切线,
(1)平行于直线y=4x-5?
(2)垂直于直线2x-6y+5=0?
(3)与x轴成135°的倾斜角?1.设f′(x0)=0,则曲线y=f(x)在点(x0,f(x0))处的切线( )
A.不存在 B.与x轴平行或重合
C.与x轴垂直 D.与x轴斜交
2.如果曲线y=f(x)在点(x0,f(x0))处的切线方程为x+2y-3=0,那么( )
A.f′(x0)>0 B.f′(x0)<0
C.f′(x0)=0 D.f′(x0)不存在
3.抛物线y=2x2在点P(1,2)处的切线l的斜率为___.
4.设曲线y=2ax3-a , 在点(1,a) 处的切线与直线2x-y+1=0
平行,则实数a的值为______
BB4思考:求过点(1,-1)与曲线y=x2+x+1相切的直线方程总结:1.导数的几何意义:2.求切线方程3.求切点(3)求过点(1,-1)与曲线y=x2+x+1相切的直线方程.解: ∵点(1,-1)不在曲线上,设切点坐标为(x0,y0),
又 y′=2x+1,则切线斜率为k=2x0+1,y0=x02+x0+1
故切线方程为y+1=(2x0+1)(x-1)
∵(x0,y0)在切线上,所以(x02+x0+1)+1=(2x0+1)(x0-1),
∴x0=3或x0=-1
当x0=3时,切线斜率k=7,
过(1,-1)的切线方程为y+1=7(x-1),即y-7x+8=0,
当x0=-1时,切线斜率k=-1,
过(1,-1)的切线方程为y+1=-1(x-1),即y+x=0.
故所求切线方程为y-7x+8=0或y+x=0. (2)求过点(-1,0)与曲线y=x2+x+1相切的直线方程. 解:∵点(-1,0)不在曲线上,设切点坐标为(x0,y0),
又 y′=2x+1,则切线斜率为k=2x0+1,y0=x02+x0+1
故切线方程为y-0=(2x0+1)(x+1)
∵(x0,y0)在切线上,所以(x02+x0+1)-0=(2x0+1)(x0+1),
∴x0=0或x0=-2
当x0=0时,切线斜率k=1,过(-1,0)的切线方程为y-0=1(x+1),
即y-x-1=0,
当x0=-2时,切线斜率k=-3,过(1,-1)的切线方程为y-0=-3(x+1), 即y+3x+3=0.
故所求切线方程为y-x-1=0或y+3x+3=0.例三:1.如图,函数 的图象在点P处的切线方程是y=-x+8, 则 ( )
A. B.1 C.2 D.0
2.曲线 在点 处的切线与两坐标轴所围成的三角形面积为( )
A、 B、 C、 D、
CD
例一:
(1)求曲线y=x2+x+1在点x=1处的切点、导数、 斜率、 切线方程 解:把x=1带入y= x2+x+1 中得y=3故切点为(1,3) ∵y′=2x+1, ∴所求切线方程为y-3=3(x-1)即3x-y=0 思考:求切线的步骤?∴切线斜率k=3∴导数y′|x=1=2×1+1=31.求切点
2.利用求导公式求导数
3.求斜率
4.利用点斜式求切线方程求切线的步骤:练一:
(1)求曲线y=x2+x在点x=1处的切点、导数、 斜率、切线方程
(2)求曲线y=2x3在点(1,2)处的切线方程.
(3)求曲线y=x2 在点(1,1)处的切线方程. 解:(1)把x=1带入y= x2+x 中得y=2故切点为(1,2) ∵y′=2x+1 ∴所求切线方程为y-2=3(x-1)即y-3x+1=0 ∴切线斜率k=3∴导数y′|x=1=2×1+1=3 (2)求曲线y=2x3在点(1,2)处的切线方程.解: ∵(1,2)在曲线上y′=6x2∴切线斜率k=y′|x=1=6×1=6∴所求切线方程为y-2=6(x-1)即y-6x+4=0(3)求曲线y=x2 在点(1,1)处的切线方程.
解:(1) ∵(1,1)在曲线上,y′=2x
∴切线斜率k=y′|x=1=2×1=2
∴所求切线方程为y-1=2(x-1),
即y-2x+1=0例二:
(1)抛物线y=x2在点P处的切线与直线4x-y+2=0
平行,求P点的坐标及切线方程.解: 设切点P点坐标为(x0,y0) ∵ y′=2x. ∴y′|x=x0=2x0又由切线与直线4x-y+2=0平行∴2x0=4,∴x0=2∵P(2,y0)在抛物线y=x2上∴y0=4∴点P的坐标为(2,4)∴切线方程为y-4=4(x-2)即4x-y-4=0(2)抛物线y=x2在点P处的切线与直线4x-y+2=0垂直,求P点的坐标.解: 设切点P点坐标为(x0,y0),
∵ y′=2x. ∴y′|x=x0=2x0,
又由切线与直线4x-y+2=0垂直,
∴4×2x0 =-1,∴x0=-
∵P(- ,y0)在抛物线y=x2上,
∴y0=
∴点P的坐标为(- , ),
练习二:在曲线y=x2上过哪一点的切线,
(1)平行于直线y=4x-5?
(2)垂直于直线2x-6y+5=0?
(3)与x轴成135°的倾斜角?1.设f′(x0)=0,则曲线y=f(x)在点(x0,f(x0))处的切线( )
A.不存在 B.与x轴平行或重合
C.与x轴垂直 D.与x轴斜交
2.如果曲线y=f(x)在点(x0,f(x0))处的切线方程为x+2y-3=0,那么( )
A.f′(x0)>0 B.f′(x0)<0
C.f′(x0)=0 D.f′(x0)不存在
3.抛物线y=2x2在点P(1,2)处的切线l的斜率为___.
4.设曲线y=2ax3-a , 在点(1,a) 处的切线与直线2x-y+1=0
平行,则实数a的值为______
BB4思考:求过点(1,-1)与曲线y=x2+x+1相切的直线方程总结:1.导数的几何意义:2.求切线方程3.求切点(3)求过点(1,-1)与曲线y=x2+x+1相切的直线方程.解: ∵点(1,-1)不在曲线上,设切点坐标为(x0,y0),
又 y′=2x+1,则切线斜率为k=2x0+1,y0=x02+x0+1
故切线方程为y+1=(2x0+1)(x-1)
∵(x0,y0)在切线上,所以(x02+x0+1)+1=(2x0+1)(x0-1),
∴x0=3或x0=-1
当x0=3时,切线斜率k=7,
过(1,-1)的切线方程为y+1=7(x-1),即y-7x+8=0,
当x0=-1时,切线斜率k=-1,
过(1,-1)的切线方程为y+1=-1(x-1),即y+x=0.
故所求切线方程为y-7x+8=0或y+x=0. (2)求过点(-1,0)与曲线y=x2+x+1相切的直线方程. 解:∵点(-1,0)不在曲线上,设切点坐标为(x0,y0),
又 y′=2x+1,则切线斜率为k=2x0+1,y0=x02+x0+1
故切线方程为y-0=(2x0+1)(x+1)
∵(x0,y0)在切线上,所以(x02+x0+1)-0=(2x0+1)(x0+1),
∴x0=0或x0=-2
当x0=0时,切线斜率k=1,过(-1,0)的切线方程为y-0=1(x+1),
即y-x-1=0,
当x0=-2时,切线斜率k=-3,过(1,-1)的切线方程为y-0=-3(x+1), 即y+3x+3=0.
故所求切线方程为y-x-1=0或y+3x+3=0.例三:1.如图,函数 的图象在点P处的切线方程是y=-x+8, 则 ( )
A. B.1 C.2 D.0
2.曲线 在点 处的切线与两坐标轴所围成的三角形面积为( )
A、 B、 C、 D、
CD
