2018年高中数学新人教B版选修1-1课件:第一章常用逻辑用语1.2.1“且”与“或”课件(20张)
文档属性
| 名称 | 2018年高中数学新人教B版选修1-1课件:第一章常用逻辑用语1.2.1“且”与“或”课件(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 81.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-22 00:00:00 | ||
图片预览








文档简介
课件20张PPT。小测:判断下列命题的真假1、28是2的倍数; 2、28是7的倍数;
3、11是143的因数; 4、11是1000的因数;
5、52>60; 6、62>60;
7、2是方程x+2=0的根; 8、2是方程x-1=0的根;
1.2.1 “且”与“或” 设命题 p: 2是质数;q: 2是偶数.
用“且”联结而构成新命题: 一般地,用逻辑联结词“且”把命题p和命题q联结起来,就得到一个新命题,
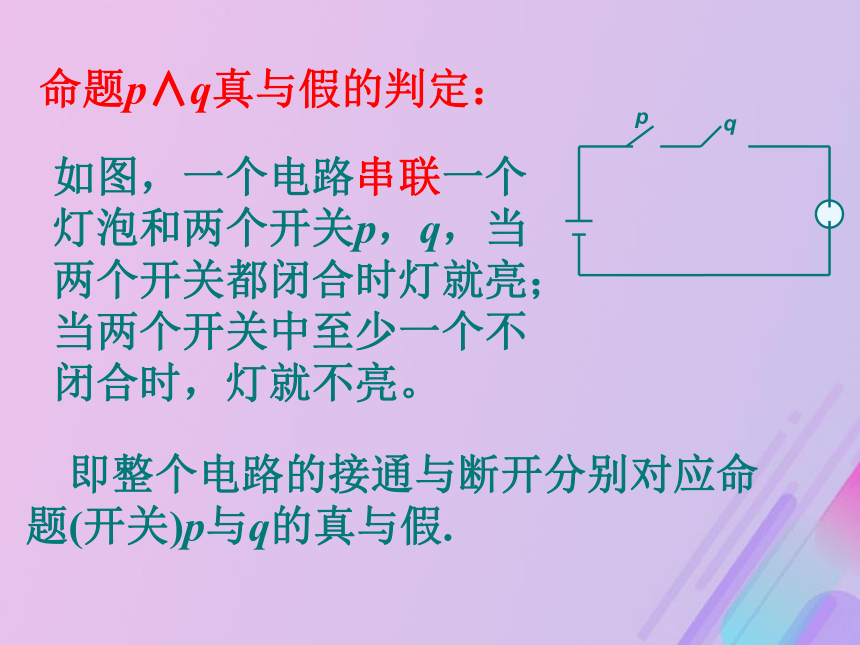
记作 p∧q. 读作“p且q”。2是质数且是偶数1. 且 逻辑联结词“且”与日常语言中的“并且” “及” “和”相当. 在日常语言中常用“且”联结两个语句。例如“他是共青团员,且学习成绩全班第一”,这个语句表达的意思是,这个同学既是共青团员,他的学习成绩又是全班第一。 显然,这个语句只有在以上两层意思都真时,它表达的才是真实的。否则只要有一层意思为假,它的表达就是不真实的.如图,一个电路串联一个灯泡和两个开关p,q,当两个开关都闭合时灯就亮;当两个开关中至少一个不闭合时,灯就不亮。 即整个电路的接通与断开分别对应命题(开关)p与q的真与假.命题p∧q真与假的判定:命题p∧q真与假的判定:规定:当p, q都是真命题时,p∧q是真命题;当p, q两个命题中有一个是假命题,p∧q是假命题。p∧q形式复合命题的真值表:真假假假小测:判断下列命题的真假1、p:28是2的倍数;(真) q:28是7的倍数; (真)
2、p:11是143的因数(真) q:11是1000的因数 (假)
3、p:52>60; (假) q:62>60; (真)
4、p:2是方程x+2=0的根(假) q:2是方程x-1=0的根(假)
例1. 把下列各组命题用“且”联结成新命题,并判断其真假:解:(1)因为lg0.1<0是真命题,lg11>0也是真命题,所以p∧q也是真命题。(1)p:lg0.1<0; q:lg11>0.
(2)p:y=cosx是周期函数;
q:y=cosx是奇函数. (2)因为y=cosx是周期函数是真命题,y=cosx是奇函数是假命题,所以p∧q是假命题例2:将下列命题用“且”联结成复合命题,并判断他们的真假。(1)p:平行四边形的对角线互相平分,q:平行四边形对角线的长相等;(2)p:菱形的对角线互相垂直, q:菱形的对角线互相平分;(3)p:35是15的倍数,q:35是7的倍数。p∧q是真p∧q是假p∧q是假例3:用逻辑联结词“且”改写下列命题,并判断它们的真假(1)1既是奇数,又是质数;(2)2和3都是质数。解:(1) 1是奇数且1是质数;假命题. (2)2是质数且3是质数;真命题.2. 或 逻辑联结词“或”的意义与日常用语中的“或者”是相当的,但是日常语言中“或者”有两种用法:其一是“不可兼”的“或”,如“向东走或向西走”,这里不可能同时向东又向西;
其二是“可兼”的“或”,如“要苹果或要香蕉”,这里可以理解为要香蕉不要苹果,也可以理解为不要香蕉要苹果,还可以理解为香蕉、苹果两者都要。设命题p:24是8的倍数;q:24是9的倍数.用“或”联结,可得新命题:24是8的倍数或24是9的倍数. 一般地,用逻辑联结词“或”把命题p和命题q联结起来,就得到一个新命题,
记作 p∨q. 读作“p或q”。 如图,一个电路并联一个灯泡和两个开关p,q,当两个开关至少一个闭合时灯就亮;当两个开关中都不闭合时,灯就不亮。命题p∨q真与假的判定:命题p∨q真与假的判定:规定:如果p, q两个命题中至少一个是真命题,则p∨q是真命题;只有当p, q两个命题都是假命题时,p∨q是假命题。p或q形式复合命题的真值表:真真真假小测:判断下列命题的真假1、p:28是2的倍数;(真) q:28是7的倍数; (真)
2、p:11是143的因数(真) q:11是1000的因数 (假)
3、p:52>60; (假) q:62>60; (真)
4、p:2是方程x+2=0的根(假) q:2是方程x-1=0的根(假)
例4. 把下列各组命题用“或”联结成新命题,并判断它们的真假.解:(1) 因为10=10为真,10<10为假,所以命题p∨q是真命题,通常记为10≤10.例5:判断下列命题的真假:(1)3≥3(3)周长相等的两个三角形全等或面积相等的两个三角形全等。(2)集合A是集合A∪B的子集或是集合A∩B的子集真命题真命题假命题例6. 判断下列命题的真假:
(1)?m∈R,m≥m;
(2)7≤7;
(3)3>2或4>5;
(4)3>2且4>5.真命题真命题真命题假命题思考:如果为p∧q真命题,那么p∨q一定是真命题吗?
反之,如果p∨q为真命题,那么p∧q一定是真命题吗?是不一定思考:如果为p∧q假命题,那么p∨q一定是假命题吗?
反之,如果p∨q为假命题,那么p∧q一定是假命题吗?是不一定小结:真值表p∧q :有假则假; p∨q:有真则真
3、11是143的因数; 4、11是1000的因数;
5、52>60; 6、62>60;
7、2是方程x+2=0的根; 8、2是方程x-1=0的根;
1.2.1 “且”与“或” 设命题 p: 2是质数;q: 2是偶数.
用“且”联结而构成新命题: 一般地,用逻辑联结词“且”把命题p和命题q联结起来,就得到一个新命题,
记作 p∧q. 读作“p且q”。2是质数且是偶数1. 且 逻辑联结词“且”与日常语言中的“并且” “及” “和”相当. 在日常语言中常用“且”联结两个语句。例如“他是共青团员,且学习成绩全班第一”,这个语句表达的意思是,这个同学既是共青团员,他的学习成绩又是全班第一。 显然,这个语句只有在以上两层意思都真时,它表达的才是真实的。否则只要有一层意思为假,它的表达就是不真实的.如图,一个电路串联一个灯泡和两个开关p,q,当两个开关都闭合时灯就亮;当两个开关中至少一个不闭合时,灯就不亮。 即整个电路的接通与断开分别对应命题(开关)p与q的真与假.命题p∧q真与假的判定:命题p∧q真与假的判定:规定:当p, q都是真命题时,p∧q是真命题;当p, q两个命题中有一个是假命题,p∧q是假命题。p∧q形式复合命题的真值表:真假假假小测:判断下列命题的真假1、p:28是2的倍数;(真) q:28是7的倍数; (真)
2、p:11是143的因数(真) q:11是1000的因数 (假)
3、p:52>60; (假) q:62>60; (真)
4、p:2是方程x+2=0的根(假) q:2是方程x-1=0的根(假)
例1. 把下列各组命题用“且”联结成新命题,并判断其真假:解:(1)因为lg0.1<0是真命题,lg11>0也是真命题,所以p∧q也是真命题。(1)p:lg0.1<0; q:lg11>0.
(2)p:y=cosx是周期函数;
q:y=cosx是奇函数. (2)因为y=cosx是周期函数是真命题,y=cosx是奇函数是假命题,所以p∧q是假命题例2:将下列命题用“且”联结成复合命题,并判断他们的真假。(1)p:平行四边形的对角线互相平分,q:平行四边形对角线的长相等;(2)p:菱形的对角线互相垂直, q:菱形的对角线互相平分;(3)p:35是15的倍数,q:35是7的倍数。p∧q是真p∧q是假p∧q是假例3:用逻辑联结词“且”改写下列命题,并判断它们的真假(1)1既是奇数,又是质数;(2)2和3都是质数。解:(1) 1是奇数且1是质数;假命题. (2)2是质数且3是质数;真命题.2. 或 逻辑联结词“或”的意义与日常用语中的“或者”是相当的,但是日常语言中“或者”有两种用法:其一是“不可兼”的“或”,如“向东走或向西走”,这里不可能同时向东又向西;
其二是“可兼”的“或”,如“要苹果或要香蕉”,这里可以理解为要香蕉不要苹果,也可以理解为不要香蕉要苹果,还可以理解为香蕉、苹果两者都要。设命题p:24是8的倍数;q:24是9的倍数.用“或”联结,可得新命题:24是8的倍数或24是9的倍数. 一般地,用逻辑联结词“或”把命题p和命题q联结起来,就得到一个新命题,
记作 p∨q. 读作“p或q”。 如图,一个电路并联一个灯泡和两个开关p,q,当两个开关至少一个闭合时灯就亮;当两个开关中都不闭合时,灯就不亮。命题p∨q真与假的判定:命题p∨q真与假的判定:规定:如果p, q两个命题中至少一个是真命题,则p∨q是真命题;只有当p, q两个命题都是假命题时,p∨q是假命题。p或q形式复合命题的真值表:真真真假小测:判断下列命题的真假1、p:28是2的倍数;(真) q:28是7的倍数; (真)
2、p:11是143的因数(真) q:11是1000的因数 (假)
3、p:52>60; (假) q:62>60; (真)
4、p:2是方程x+2=0的根(假) q:2是方程x-1=0的根(假)
例4. 把下列各组命题用“或”联结成新命题,并判断它们的真假.解:(1) 因为10=10为真,10<10为假,所以命题p∨q是真命题,通常记为10≤10.例5:判断下列命题的真假:(1)3≥3(3)周长相等的两个三角形全等或面积相等的两个三角形全等。(2)集合A是集合A∪B的子集或是集合A∩B的子集真命题真命题假命题例6. 判断下列命题的真假:
(1)?m∈R,m≥m;
(2)7≤7;
(3)3>2或4>5;
(4)3>2且4>5.真命题真命题真命题假命题思考:如果为p∧q真命题,那么p∨q一定是真命题吗?
反之,如果p∨q为真命题,那么p∧q一定是真命题吗?是不一定思考:如果为p∧q假命题,那么p∨q一定是假命题吗?
反之,如果p∨q为假命题,那么p∧q一定是假命题吗?是不一定小结:真值表p∧q :有假则假; p∨q:有真则真
