2018年高中数学新人教B版选修1-1课件:第一章常用逻辑用语1.3.1推出与充分条件、必要条件课件(18张)
文档属性
| 名称 | 2018年高中数学新人教B版选修1-1课件:第一章常用逻辑用语1.3.1推出与充分条件、必要条件课件(18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 163.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-22 00:00:00 | ||
图片预览






文档简介
课件18张PPT。推出与充分条件、必要条件请同学们判断下列命题的真假。
(1) 如果x=y,则x2=y2
(2)如果x2=y2 ,则x=y
(3)如果ab = 0,则a = 0
(4)如果a = 0 ,则ab = 0
(5)如果x=1或x=2,则x2-3x+2=0
(6)如果x2-3x+2=0 ,则x=1或x=2
(1) (4) (5) (6)真(2) (3) 假 若p 则q读作: p推出q读作: p推不出q充分条件与必要条件:a = 0 ab=0
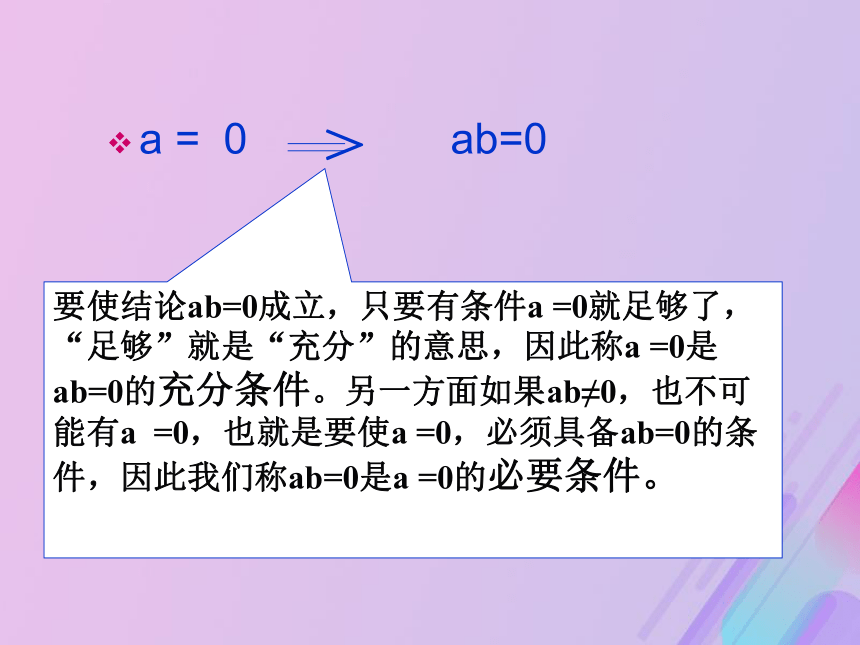
要使结论ab=0成立,只要有条件a =0就足够了,“足够”就是“充分”的意思,因此称a =0是ab=0的充分条件。另一方面如果ab≠0,也不可能有a =0,也就是要使a =0,必须具备ab=0的条件,因此我们称ab=0是a =0的必要条件。
例1:指出下列各组命题中,p是q的什么条件, q是p的什么条件:
(1) p:x-1=0;q:(x-1)(x+2)=0.
(2) p:两条直线平行;q:内错角相等.
(3) p:a>b;q:a2>b2
一般地,如果既有p q,又有q p,就记作p q,这时,p既是q的充分条件,又是q的必要条件,我们就说p是q的充分必要条件,简称充要条件. 充要条件由上述各组命题的充分条件、必要条件的判断过程,可知两个命题间的因果关系应有几种? p q 但 q pp是q的充分不必要条件p是q的必要不充分条件p是q的充要条件p是q的既不充分又不必要条件p q 但q pp q p q 且 q pP是q的什么条件的判断:思 考:已知:若q p,那么:p是q的( ) A、充分非必要条件 B、必要非充分条件
C、充要条件 D、既非充分也非必要条件要小心哦?BP足以导致q,也就是说条件p充分了;
q是p成立所 必须具备的前提。 从集合角度理解:例2.填表例3:如图1,有一个圆A,在其内又含有一个圆B. 请回答 ⑴命题:若“A为绿色”,则“B为绿色”中,“A为绿色”是“B为绿色”的什么条件;
“B为绿色”又是“A为绿色”的什么条件. ⑵命题:若“红点在B内”,则“红点一定在A内”中,“红点在B内”是“红点在A内”的什么条件;
“红点在A内”又是“红点在B内”的什么条件. 例4:已知p是q的充分条件,s是p的充分条件,r是q 的必要条件,又是s的充分条件,问s是q的什么条件?p是s 的什么条件? 【分析】本题中各条件都是抽象的,不容易得出它们之间的关系,可以借助图象直观表示,将有助于作出正确的判断。但要注意递推符号的正确使用和传递关系。课堂小结:(1)充分条件、必要条件、充分必要条件的概念.
(2)判断充分、必要条件的基本方法.
探讨下列生活中名言名句的充分、必要关系。( 1 )水滴石穿( 2 ) 骄兵必败( 3 ) 有志者事竟成( 4 ) 头发长,见识短谢谢各位!谢谢各位!
(1) 如果x=y,则x2=y2
(2)如果x2=y2 ,则x=y
(3)如果ab = 0,则a = 0
(4)如果a = 0 ,则ab = 0
(5)如果x=1或x=2,则x2-3x+2=0
(6)如果x2-3x+2=0 ,则x=1或x=2
(1) (4) (5) (6)真(2) (3) 假 若p 则q读作: p推出q读作: p推不出q充分条件与必要条件:a = 0 ab=0
要使结论ab=0成立,只要有条件a =0就足够了,“足够”就是“充分”的意思,因此称a =0是ab=0的充分条件。另一方面如果ab≠0,也不可能有a =0,也就是要使a =0,必须具备ab=0的条件,因此我们称ab=0是a =0的必要条件。
例1:指出下列各组命题中,p是q的什么条件, q是p的什么条件:
(1) p:x-1=0;q:(x-1)(x+2)=0.
(2) p:两条直线平行;q:内错角相等.
(3) p:a>b;q:a2>b2
一般地,如果既有p q,又有q p,就记作p q,这时,p既是q的充分条件,又是q的必要条件,我们就说p是q的充分必要条件,简称充要条件. 充要条件由上述各组命题的充分条件、必要条件的判断过程,可知两个命题间的因果关系应有几种? p q 但 q pp是q的充分不必要条件p是q的必要不充分条件p是q的充要条件p是q的既不充分又不必要条件p q 但q pp q p q 且 q pP是q的什么条件的判断:思 考:已知:若q p,那么:p是q的( ) A、充分非必要条件 B、必要非充分条件
C、充要条件 D、既非充分也非必要条件要小心哦?BP足以导致q,也就是说条件p充分了;
q是p成立所 必须具备的前提。 从集合角度理解:例2.填表例3:如图1,有一个圆A,在其内又含有一个圆B. 请回答 ⑴命题:若“A为绿色”,则“B为绿色”中,“A为绿色”是“B为绿色”的什么条件;
“B为绿色”又是“A为绿色”的什么条件. ⑵命题:若“红点在B内”,则“红点一定在A内”中,“红点在B内”是“红点在A内”的什么条件;
“红点在A内”又是“红点在B内”的什么条件. 例4:已知p是q的充分条件,s是p的充分条件,r是q 的必要条件,又是s的充分条件,问s是q的什么条件?p是s 的什么条件? 【分析】本题中各条件都是抽象的,不容易得出它们之间的关系,可以借助图象直观表示,将有助于作出正确的判断。但要注意递推符号的正确使用和传递关系。课堂小结:(1)充分条件、必要条件、充分必要条件的概念.
(2)判断充分、必要条件的基本方法.
探讨下列生活中名言名句的充分、必要关系。( 1 )水滴石穿( 2 ) 骄兵必败( 3 ) 有志者事竟成( 4 ) 头发长,见识短谢谢各位!谢谢各位!
