2018年高中数学第2章平面解析几何初步2.1.3两条直线的平行与垂直课件4苏教版必修2(14张)
文档属性
| 名称 | 2018年高中数学第2章平面解析几何初步2.1.3两条直线的平行与垂直课件4苏教版必修2(14张) |  | |
| 格式 | zip | ||
| 文件大小 | 140.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-22 08:38:44 | ||
图片预览






文档简介
课件14张PPT。两直线的位置关系---两直线平行课首自学:1.你知道用什么来刻画直线的倾斜程度吗?
2.那能否用倾斜角,斜率来刻画两
条直线的位置关系呢?
课中共学:结论:已知直线l1∥l2,
①若l1,l2的斜率存在,
设l1:y=k1x+b1,l2:y=k2x+b2
则k1=k2,且b1≠b2;
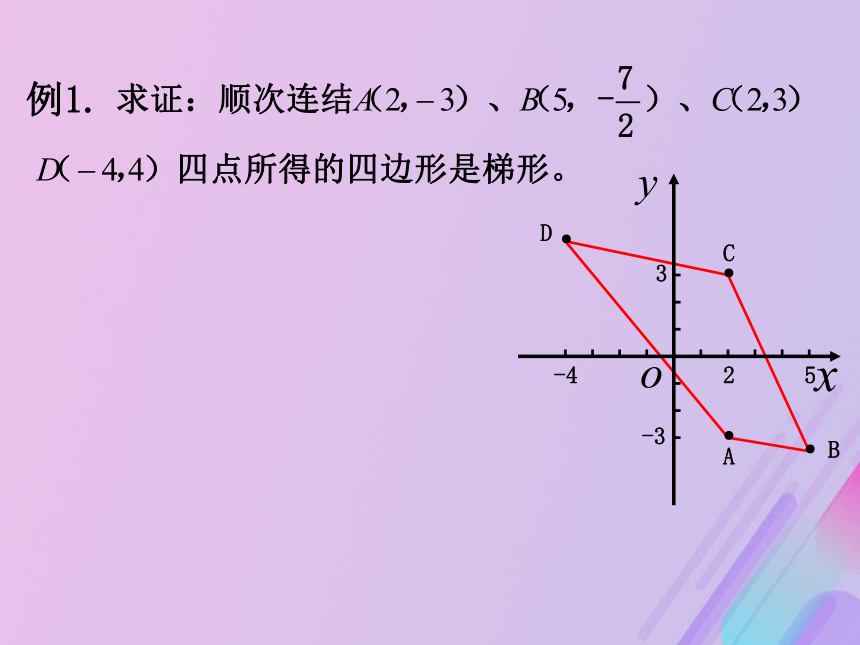
②l1,l2的斜率均不存在, a1 ≠ a2.例1. ∴直线AB平行于CD,而直线BC与DA不平行。已知直线l1∥l2,
③若l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,(A1,B1不全为零,A2,B2不全为零),则A1B2-A2B1=0且 B1C2-B2C1≠0
或 A1B2-A2B1=0且A1C2 - A2C1≠0
结论:y=3x+1与2y-6x+4=0
4x-3y=5与8x-6y=10
x+y-1=0与2x-y+1=0
x+1=0与x-4=0
练习:例2.已知两条直线:l1:x+ay+3=0与
l2: ax+4y+6=0,a为何值时,两直线平行?
练习:直线l1:2x+(m+1)y+4=0与l2:mx+3y-2=0平行,求m的值.注意:练习:求过点A(2,-3),且与直线2x+y-5=0平行的直线的方程.
1.已知直线l1:mx+y-(m+1)=0,l2:x+my-2m=0,当m为何值时,直线l1与l2互相平行?课尾检学:2.若直线l与直线2x+y-5=0平行,并且在两坐标轴截距之和为6.求直线l的方程.
小结:2.利用两直线的一般式方程判断两直线的平行关系.
l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,则
l1∥l2 ? A1B2-B1A2=0,且A1C2-C1A2≠0或B1C2-B2C1≠0 .1.利用两直线的斜率关系判断两直线的平行关系.
①斜率存在, l1∥l2 ? k1=k2,且截距不等;
②斜率都不存在.
注:若用斜率判断,须对斜率的存在性加以分类讨论.3.利用直线系解题.
已知l1∥l2,且l1的方程为Ax+By+C=0,则设l2的方程为Ax+By+m=0(C ≠m) 。
2.那能否用倾斜角,斜率来刻画两
条直线的位置关系呢?
课中共学:结论:已知直线l1∥l2,
①若l1,l2的斜率存在,
设l1:y=k1x+b1,l2:y=k2x+b2
则k1=k2,且b1≠b2;
②l1,l2的斜率均不存在, a1 ≠ a2.例1. ∴直线AB平行于CD,而直线BC与DA不平行。已知直线l1∥l2,
③若l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,(A1,B1不全为零,A2,B2不全为零),则A1B2-A2B1=0且 B1C2-B2C1≠0
或 A1B2-A2B1=0且A1C2 - A2C1≠0
结论:y=3x+1与2y-6x+4=0
4x-3y=5与8x-6y=10
x+y-1=0与2x-y+1=0
x+1=0与x-4=0
练习:例2.已知两条直线:l1:x+ay+3=0与
l2: ax+4y+6=0,a为何值时,两直线平行?
练习:直线l1:2x+(m+1)y+4=0与l2:mx+3y-2=0平行,求m的值.注意:练习:求过点A(2,-3),且与直线2x+y-5=0平行的直线的方程.
1.已知直线l1:mx+y-(m+1)=0,l2:x+my-2m=0,当m为何值时,直线l1与l2互相平行?课尾检学:2.若直线l与直线2x+y-5=0平行,并且在两坐标轴截距之和为6.求直线l的方程.
小结:2.利用两直线的一般式方程判断两直线的平行关系.
l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,则
l1∥l2 ? A1B2-B1A2=0,且A1C2-C1A2≠0或B1C2-B2C1≠0 .1.利用两直线的斜率关系判断两直线的平行关系.
①斜率存在, l1∥l2 ? k1=k2,且截距不等;
②斜率都不存在.
注:若用斜率判断,须对斜率的存在性加以分类讨论.3.利用直线系解题.
已知l1∥l2,且l1的方程为Ax+By+C=0,则设l2的方程为Ax+By+m=0(C ≠m) 。
