2018年高中数学第2章平面解析几何初步2.1.5平面上两点间的距离课件2苏教版必修2(14张)
文档属性
| 名称 | 2018年高中数学第2章平面解析几何初步2.1.5平面上两点间的距离课件2苏教版必修2(14张) |  | |
| 格式 | zip | ||
| 文件大小 | 151.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-22 08:39:11 | ||
图片预览




文档简介
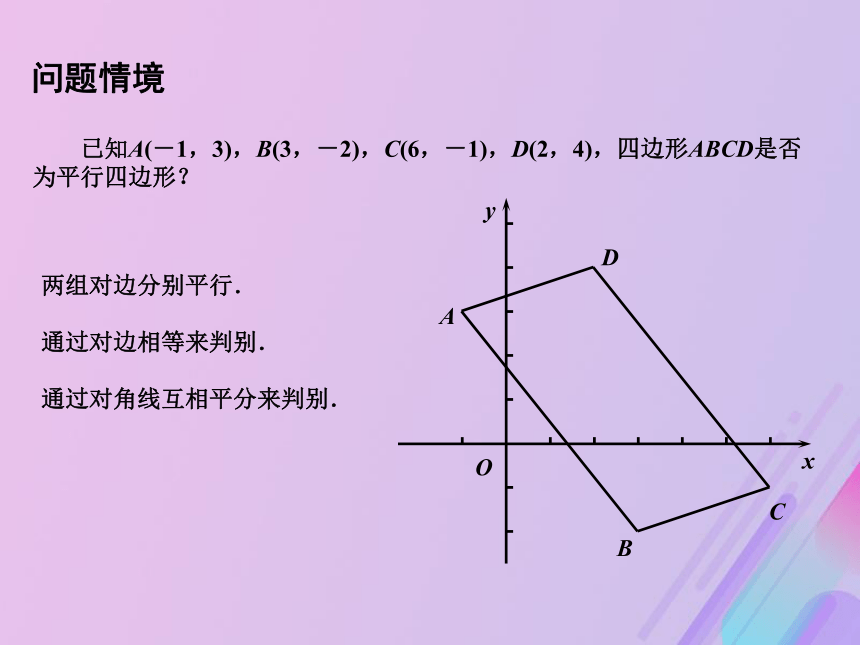
课件14张PPT。2.1.5 平面上两点间的距离 已知A(-1,3),B(3,-2),C(6,-1),D(2,4),四边形ABCD是否为平行四边形? xyOABCD两组对边分别平行.通过对边相等来判别. 通过对角线互相平分来判别. 问题情境x轴上两点P1(x1,0), P2(x2,0)的距离.
| P1P2|=|x2-x1|.
y轴上两点Q1(0,y1), Q2(0,y2)的距离.
| Q1Q2|=|y2-y1|.
推广:
M1(x1,a),M2(x2,a)的距离| M1M2|=|x2-x1|.
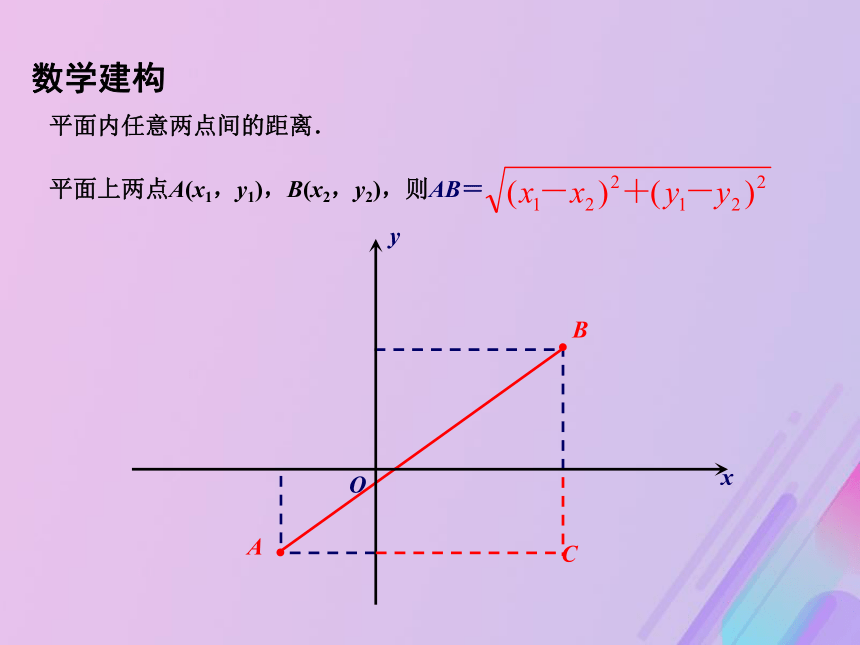
N1(0,y1), N2(0,y2)的距离| N1N2|=|y2-y1|.xyOP1P2M1M2N1N2Q1Q2数学建构坐标轴上两点间的距离.平面上两点A(x1,y1),B(x2,y2),则AB=数学建构平面内任意两点间的距离.例1.(1)求(-1,3),(2,5)两点间的距离;
(2)若(0,10),(a,-5)两点间的距离是,求实数a的值. 数学应用(1)已知(a,0)到(5,12)的距离为13,则a=________.
(2)若x轴上的点M到原点及到点(5,-3)的距离相等,则M的坐标为
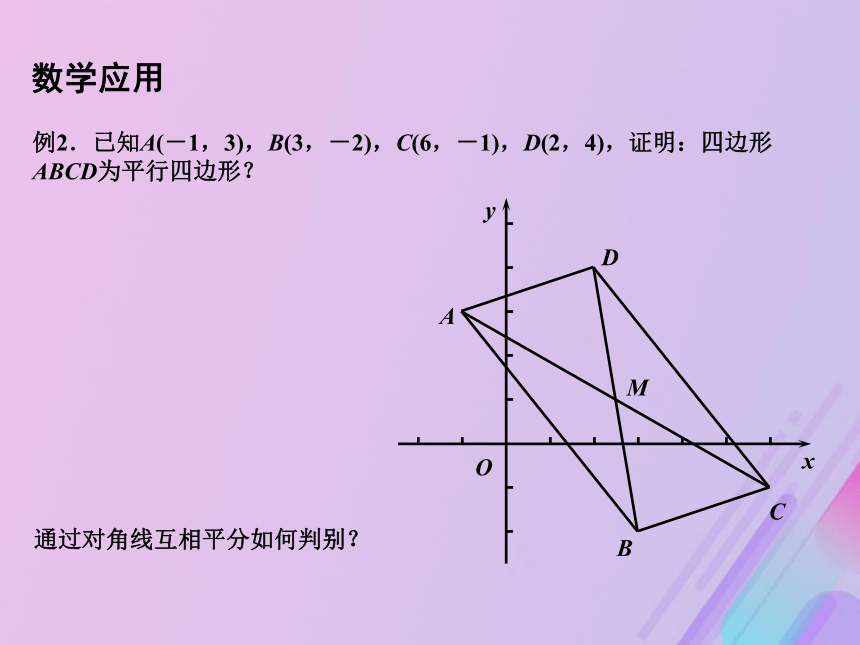
______ .例2.已知A(-1,3),B(3,-2),C(6,-1),D(2,4),证明:四边形ABCD为平行四边形? xyOABCD通过对角线互相平分如何判别?M数学应用x-2y+4=0数学建构中点坐标公式.练习:一直线被两坐标轴所截线段中点坐标为(-2,1),则该直线的方程为
_______________. 一般地,对于平面上的两点P1(x1,y1),P2(x2,y2),线段P1P2的中点是M(x0,y0),则:x0=y0=xyOP1(x1,y1)P2(x2,y2)P0(x0,y0)证明分两步完成:第一步 证明点M在直线P1P2上第二步 证明P1M= MP2. 例2.已知△ABC的顶点坐标为A(-1,5),B(-2,-1), C(4,7),求BC边上的中线AM的长和AM所在直线的方程. xyOABCM思考:如何求△ABC的重心坐标呢?N数学应用 已知平行四边形ABCD的三个顶点分别是A(1,2),B(-1,3), C(-3,-1),求第四个顶点D 的坐标.xyOABC数学应用 已知矩形ABCD两个顶点A(-1,3),B(-3,1),若它的对角线交点M在x轴上,求C,D两点的坐标. 数学应用 已知点A(1,2),B(2, ),试在x轴上求一点P,使PA=PB,并求此时PA的值.数学应用 已知A,B两点都在直线y=2x+1上,且A,B两点的横坐标之差为 ,A,B两点之间的距离为__________. 数学应用例4.已知△ABC是直角三角形,斜边BC的中点为M,建立适当的坐标
系,证明:AM= BC. 数学应用AB=设A(x1,y1),B(x2,y2)是平面上任意两点.设线段AB的中点是P(x0,y0),则:x0=y0=小结1.平面内两点间距离公式. 2.中点坐标公式.
| P1P2|=|x2-x1|.
y轴上两点Q1(0,y1), Q2(0,y2)的距离.
| Q1Q2|=|y2-y1|.
推广:
M1(x1,a),M2(x2,a)的距离| M1M2|=|x2-x1|.
N1(0,y1), N2(0,y2)的距离| N1N2|=|y2-y1|.xyOP1P2M1M2N1N2Q1Q2数学建构坐标轴上两点间的距离.平面上两点A(x1,y1),B(x2,y2),则AB=数学建构平面内任意两点间的距离.例1.(1)求(-1,3),(2,5)两点间的距离;
(2)若(0,10),(a,-5)两点间的距离是,求实数a的值. 数学应用(1)已知(a,0)到(5,12)的距离为13,则a=________.
(2)若x轴上的点M到原点及到点(5,-3)的距离相等,则M的坐标为
______ .例2.已知A(-1,3),B(3,-2),C(6,-1),D(2,4),证明:四边形ABCD为平行四边形? xyOABCD通过对角线互相平分如何判别?M数学应用x-2y+4=0数学建构中点坐标公式.练习:一直线被两坐标轴所截线段中点坐标为(-2,1),则该直线的方程为
_______________. 一般地,对于平面上的两点P1(x1,y1),P2(x2,y2),线段P1P2的中点是M(x0,y0),则:x0=y0=xyOP1(x1,y1)P2(x2,y2)P0(x0,y0)证明分两步完成:第一步 证明点M在直线P1P2上第二步 证明P1M= MP2. 例2.已知△ABC的顶点坐标为A(-1,5),B(-2,-1), C(4,7),求BC边上的中线AM的长和AM所在直线的方程. xyOABCM思考:如何求△ABC的重心坐标呢?N数学应用 已知平行四边形ABCD的三个顶点分别是A(1,2),B(-1,3), C(-3,-1),求第四个顶点D 的坐标.xyOABC数学应用 已知矩形ABCD两个顶点A(-1,3),B(-3,1),若它的对角线交点M在x轴上,求C,D两点的坐标. 数学应用 已知点A(1,2),B(2, ),试在x轴上求一点P,使PA=PB,并求此时PA的值.数学应用 已知A,B两点都在直线y=2x+1上,且A,B两点的横坐标之差为 ,A,B两点之间的距离为__________. 数学应用例4.已知△ABC是直角三角形,斜边BC的中点为M,建立适当的坐标
系,证明:AM= BC. 数学应用AB=设A(x1,y1),B(x2,y2)是平面上任意两点.设线段AB的中点是P(x0,y0),则:x0=y0=小结1.平面内两点间距离公式. 2.中点坐标公式.
