2018年高中数学第2章平面解析几何初步2.1.6点到直线的距离课件3苏教版必修2(15张)
文档属性
| 名称 | 2018年高中数学第2章平面解析几何初步2.1.6点到直线的距离课件3苏教版必修2(15张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-22 00:00:00 | ||
图片预览






文档简介
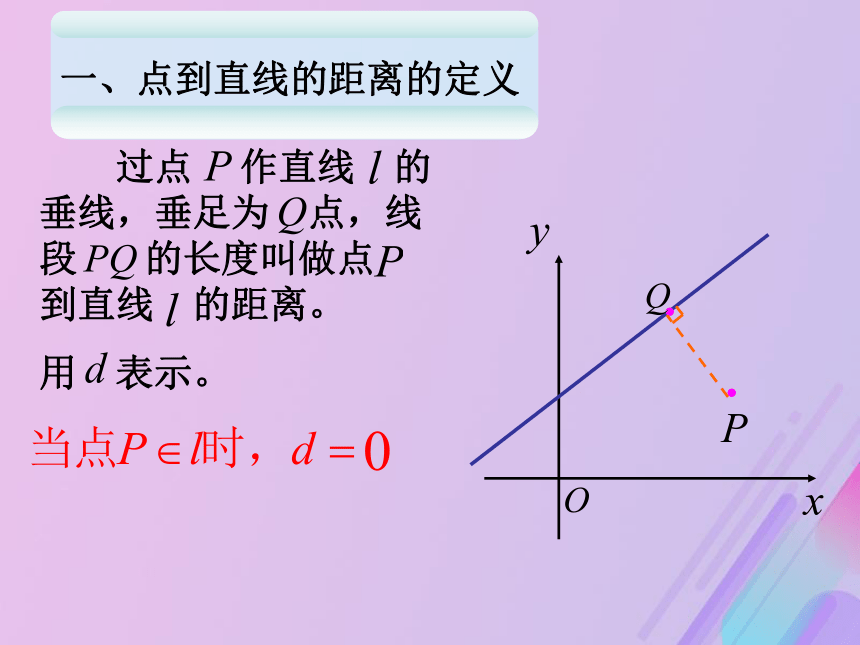
课件15张PPT。点到直线的距离一、点到直线的距离的定义问题一、求点到下列直线的距离:提问:
问题一:求线段长度可以构造图形吗? 问题二:什么图形?如何构造?问题三:三角形第三个顶点选在什么位置? 问题四:特殊情况与一般情况有联系吗? ?小结:
方法一:利用定义。
方法二:构造三角形,利用边角关系,借助直线的倾斜角。方法一:利用定义(算法如下) 确定直线 的斜率求过点 P且垂直于 的直线 的方程 求 与 的交点求出点 与点 的距离 求与 垂直直线的斜率
·方法二、利用等面积法(算法如下) 利用勾股定理求出 二、点到直线的距离公式 点 到直线
( )的距离为提问:
①上式是由 条件下得出,
对 成立吗?
②点P在直线上成立吗?
③公式结构特点是什么?用公式时直线方程是什么形式?
?例. 求点P(?1,2)到下列直线的距离:
(1)y=-2x+10;(2)3x=2;(3)2y+1=0用点到直线的距离公式,先将直线方程化为一般式。?P特殊位置的直线可数形结合解决。?P三、公式应用求点P(3,1)到下列直线的距离:
(1)3x+4y?5=0;(2)5x+2=0;(3)3y?1=0课堂练习:2. 已知△ABC的三个顶点坐标分别为A(2,1)、B(5,3)、C(?1,5),求△ABC的 BC边上的高。 点A到BC所在直线的距离。解:直线BC的方程为x+3y?14=0,四、总结(1)知识概括:
(2)数学思想方法:(3)收获:类比、转化、数形结合、特殊到一般等思想方法。点到直线的距离公式的推导和应用。字母的运算。五、作业 (1)写出求点到直线距离公式的多种算法,并选 择你最喜欢的一种算法推导公式。
(2)课本习题2.1的7、9、10、11。
问题一:求线段长度可以构造图形吗? 问题二:什么图形?如何构造?问题三:三角形第三个顶点选在什么位置? 问题四:特殊情况与一般情况有联系吗? ?小结:
方法一:利用定义。
方法二:构造三角形,利用边角关系,借助直线的倾斜角。方法一:利用定义(算法如下) 确定直线 的斜率求过点 P且垂直于 的直线 的方程 求 与 的交点求出点 与点 的距离 求与 垂直直线的斜率
·方法二、利用等面积法(算法如下) 利用勾股定理求出 二、点到直线的距离公式 点 到直线
( )的距离为提问:
①上式是由 条件下得出,
对 成立吗?
②点P在直线上成立吗?
③公式结构特点是什么?用公式时直线方程是什么形式?
?例. 求点P(?1,2)到下列直线的距离:
(1)y=-2x+10;(2)3x=2;(3)2y+1=0用点到直线的距离公式,先将直线方程化为一般式。?P特殊位置的直线可数形结合解决。?P三、公式应用求点P(3,1)到下列直线的距离:
(1)3x+4y?5=0;(2)5x+2=0;(3)3y?1=0课堂练习:2. 已知△ABC的三个顶点坐标分别为A(2,1)、B(5,3)、C(?1,5),求△ABC的 BC边上的高。 点A到BC所在直线的距离。解:直线BC的方程为x+3y?14=0,四、总结(1)知识概括:
(2)数学思想方法:(3)收获:类比、转化、数形结合、特殊到一般等思想方法。点到直线的距离公式的推导和应用。字母的运算。五、作业 (1)写出求点到直线距离公式的多种算法,并选 择你最喜欢的一种算法推导公式。
(2)课本习题2.1的7、9、10、11。
