2018年高中数学第1章立体几何初步1.2.1平面的基本性质课件2苏教版必修2(31张)
文档属性
| 名称 | 2018年高中数学第1章立体几何初步1.2.1平面的基本性质课件2苏教版必修2(31张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-23 08:18:47 | ||
图片预览











文档简介
课件31张PPT。§1.2.1
平面的基本性质(一)将一把直尺置于桌面上,通过是否漏光就能检查桌面是否平整;
用两个合页和一把锁就可以固定一扇门,
为什么?问题2:平静的湖面,广阔的草原,会给你留下怎样的印象呢? 很大、很平.问题3:还有哪些面留给我们平面的形象
呢?桌面、黑板、地面等.1. 平面的特点以上例子给我们“平面”的直观,平面是一个不加定义的概念,具有“无大小”、“无限延展”、“无厚薄”的特点.【例1】已知命题:
①10个平面重叠起来,要比5个平面
重叠起来厚;
②有一个平面的长是50m,宽是20m;
③黑板面是平面;
④平面是绝对的平,没有大小、没有
厚度,可以无限延展的抽象的数学
概念.
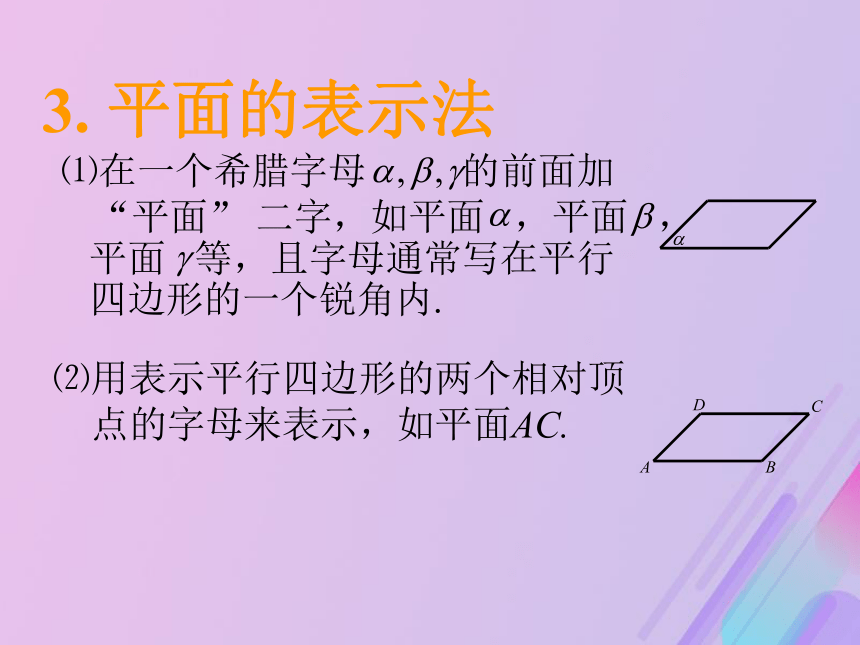
其中正确的的命题是__________.④问题3:如何形象直观的在纸上表示平面?数学中怎样来表示一个平坦的、没有薄厚的、而且无限延伸的画面呢?想一想?通常画平行四边形来表示平面.2. 平面的画法3. 平面的表示法⑴在一个希腊字母 的前面加
“平面” 二字,如平面 ,平面 ,
平面 等,且字母通常写在平行
四边形的一个锐角内.⑵用表示平行四边形的两个相对顶
点的字母来表示,如平面AC.如果把桌面看作一个平面,把你的直尺看作
是一条直线的话,你觉得在什么情况下,
才能使你的直尺所代表的直线上所有的点都
能在桌面上?
··数学实验1观察下列问题,你能得到什么结论?数学实验1结论:如果一条直线上的两个点在一个平面内,
那么这条直线上所有的点都在这个平面内.文字语言:
公理1:如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内.图形语言:4. 平面的基本性质 空间中的点、直线、平面的位置关系,可
以借用集合中的符号来表示.
例如:在长方体 ABCD—A1B1C1D1中P ∈ AB
M ∈ 平面ACAB∩BC = B
文字语言:
公理1:如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内.图形语言:符号语言:公理1可以帮助我们解决哪些几何问题?⑴判定直线或点是否在平面内;
⑵说明平面的无限延伸;
(3) 检验平面。将一把直尺置于桌面上,通过是否漏光就能
检查桌面是否平整.把一本书的一角立在桌面上,观察这本书所在的平面与桌面所在平面有几个公共点?数学试验2如果两个平面有一个公共点,那么它们还有其他公共点,这些公共点的集合是经过这个公共点的一条直线.数学实验2结论:文字语言:图形语言:符号语言:公理2.如果两个平面有一个公共点,那么它们还有其它公共点,这些公共点的集合是经过这个公共点的一条直线。
公理2可以帮助我们解决哪些几何问题?1、判定点在直线上;
2、判定两个平面相交;
3、找两个平面的交线的依据;
4、说明平面的无限延伸。
数学试验3观察思考:照相机的支架为什么只需三条腿?数学试验3观察思考:照相机的支架为什么只需三条腿?结论:经过不在同一条直线上的三点,有且只有一个平面.公理3:经过不在同一条直线上的三点,有且
只有一个平面.图形语言:符号语言:如何理解公理3中的“有且只有一个”?“有”是说图形存在,“只有一个”是说图形惟一.公理3可以帮助我们解决哪些几何问题?⑴确定平面;
⑵证明两个平面重合.用两个合页和一把锁就可以固定一扇门BD1课 堂 练 习课堂练习1.平面的概念、表示和记法;2.空间中点、线、面位置关系的图3.平面的三个公理及用途.形及符号表示;谢谢指导!
平面的基本性质(一)将一把直尺置于桌面上,通过是否漏光就能检查桌面是否平整;
用两个合页和一把锁就可以固定一扇门,
为什么?问题2:平静的湖面,广阔的草原,会给你留下怎样的印象呢? 很大、很平.问题3:还有哪些面留给我们平面的形象
呢?桌面、黑板、地面等.1. 平面的特点以上例子给我们“平面”的直观,平面是一个不加定义的概念,具有“无大小”、“无限延展”、“无厚薄”的特点.【例1】已知命题:
①10个平面重叠起来,要比5个平面
重叠起来厚;
②有一个平面的长是50m,宽是20m;
③黑板面是平面;
④平面是绝对的平,没有大小、没有
厚度,可以无限延展的抽象的数学
概念.
其中正确的的命题是__________.④问题3:如何形象直观的在纸上表示平面?数学中怎样来表示一个平坦的、没有薄厚的、而且无限延伸的画面呢?想一想?通常画平行四边形来表示平面.2. 平面的画法3. 平面的表示法⑴在一个希腊字母 的前面加
“平面” 二字,如平面 ,平面 ,
平面 等,且字母通常写在平行
四边形的一个锐角内.⑵用表示平行四边形的两个相对顶
点的字母来表示,如平面AC.如果把桌面看作一个平面,把你的直尺看作
是一条直线的话,你觉得在什么情况下,
才能使你的直尺所代表的直线上所有的点都
能在桌面上?
··数学实验1观察下列问题,你能得到什么结论?数学实验1结论:如果一条直线上的两个点在一个平面内,
那么这条直线上所有的点都在这个平面内.文字语言:
公理1:如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内.图形语言:4. 平面的基本性质 空间中的点、直线、平面的位置关系,可
以借用集合中的符号来表示.
例如:在长方体 ABCD—A1B1C1D1中P ∈ AB
M ∈ 平面ACAB∩BC = B
文字语言:
公理1:如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内.图形语言:符号语言:公理1可以帮助我们解决哪些几何问题?⑴判定直线或点是否在平面内;
⑵说明平面的无限延伸;
(3) 检验平面。将一把直尺置于桌面上,通过是否漏光就能
检查桌面是否平整.把一本书的一角立在桌面上,观察这本书所在的平面与桌面所在平面有几个公共点?数学试验2如果两个平面有一个公共点,那么它们还有其他公共点,这些公共点的集合是经过这个公共点的一条直线.数学实验2结论:文字语言:图形语言:符号语言:公理2.如果两个平面有一个公共点,那么它们还有其它公共点,这些公共点的集合是经过这个公共点的一条直线。
公理2可以帮助我们解决哪些几何问题?1、判定点在直线上;
2、判定两个平面相交;
3、找两个平面的交线的依据;
4、说明平面的无限延伸。
数学试验3观察思考:照相机的支架为什么只需三条腿?数学试验3观察思考:照相机的支架为什么只需三条腿?结论:经过不在同一条直线上的三点,有且只有一个平面.公理3:经过不在同一条直线上的三点,有且
只有一个平面.图形语言:符号语言:如何理解公理3中的“有且只有一个”?“有”是说图形存在,“只有一个”是说图形惟一.公理3可以帮助我们解决哪些几何问题?⑴确定平面;
⑵证明两个平面重合.用两个合页和一把锁就可以固定一扇门BD1课 堂 练 习课堂练习1.平面的概念、表示和记法;2.空间中点、线、面位置关系的图3.平面的三个公理及用途.形及符号表示;谢谢指导!
