2018年高中数学第2章平面解析几何初步2.1.1直线的斜率课件3苏教版必修2(15张)
文档属性
| 名称 | 2018年高中数学第2章平面解析几何初步2.1.1直线的斜率课件3苏教版必修2(15张) |

|
|
| 格式 | zip | ||
| 文件大小 | 496.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-23 00:00:00 | ||
图片预览




文档简介
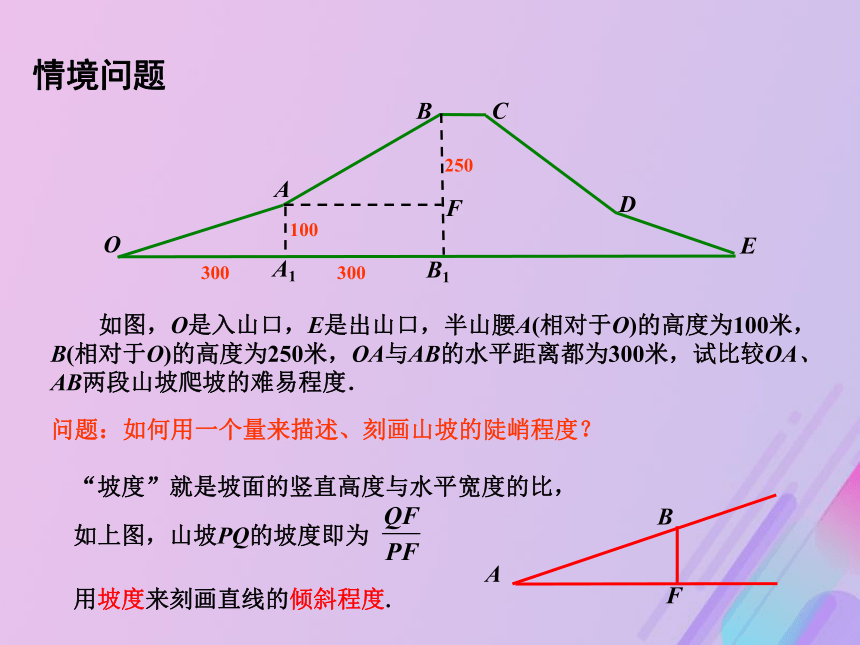
课件15张PPT。 直线的斜率情境创设现实世界中,到处有美妙的曲线.从飞逝的流星到雨后彩虹,从古代的石拱桥到现代的立交桥……这些曲线都和方程息息相关. 情境问题问题1 .如何将这些曲线与方程联系起来呢? 引进平面直角坐标系,用有序数对(x,y)表示平面内的点.根据曲线的几何性质,可以得到关于x,y的一个代数方程f(x,y)=0.反过来,把代数方程f(x,y)=0的解(x,y)看做平面上点的坐标,这些点的集合是一条曲线. 如果代数与几何各自分开发展,那么它的进步将十分缓慢,而且应用范围也很有限.但若两互相结合而共同发展,则就者会相互加强,并以快速的步伐向着完美化的方向猛进.——拉格朗日 解析几何的本质是用代数方法研究几何图形的性质,即通过引进直角坐标系,建立点与坐标、曲线与方程之间的对应关系,将几何问题转化为代数问题,从而用代数方法研究几何问题.解析几何的基本思想是数形结合. 情境问题问题2 .解析几何与几何的本质区别是什么呢? 本章研究的基本几何图形——直线与圆 本章研究的基本问题: 1.如何建立它们的方程? 2.如何通过方程来研究它们的性质?——位置关系(平行、相交、…) 本节课研究的问题: 1.如何确定直线?2.如何用一个代数的量来刻画直线的方向(倾斜程度)? ——两个要素(两点、点与方向) 如图,O是入山口,E是出山口,半山腰A(相对于O)的高度为100米,B(相对于O)的高度为250米,OA与AB的水平距离都为300米,试比较OA、AB两段山坡爬坡的难易程度.情境问题100250300300F问题:如何用一个量来描述、刻画山坡的陡峭程度?“坡度”就是坡面的竖直高度与水平宽度的比,
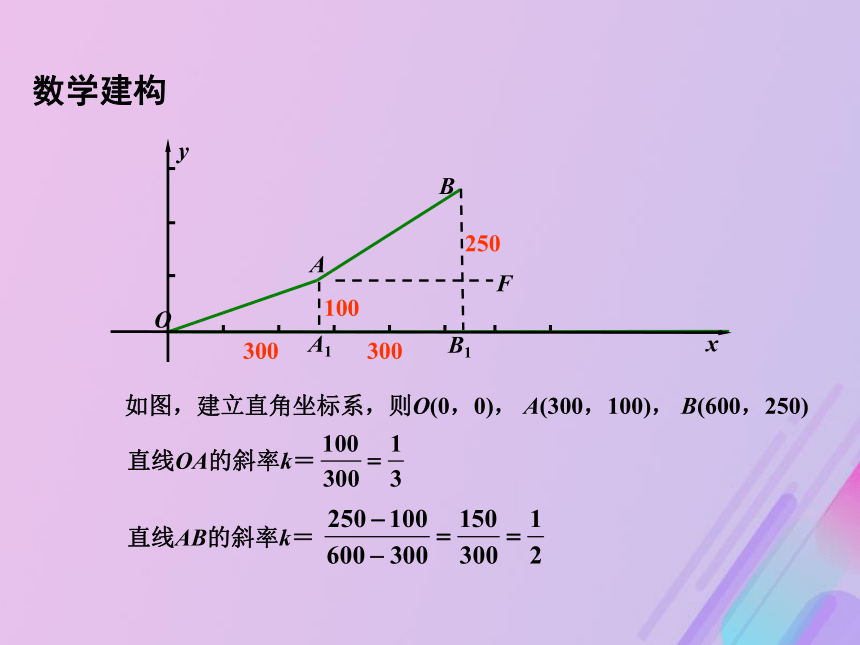
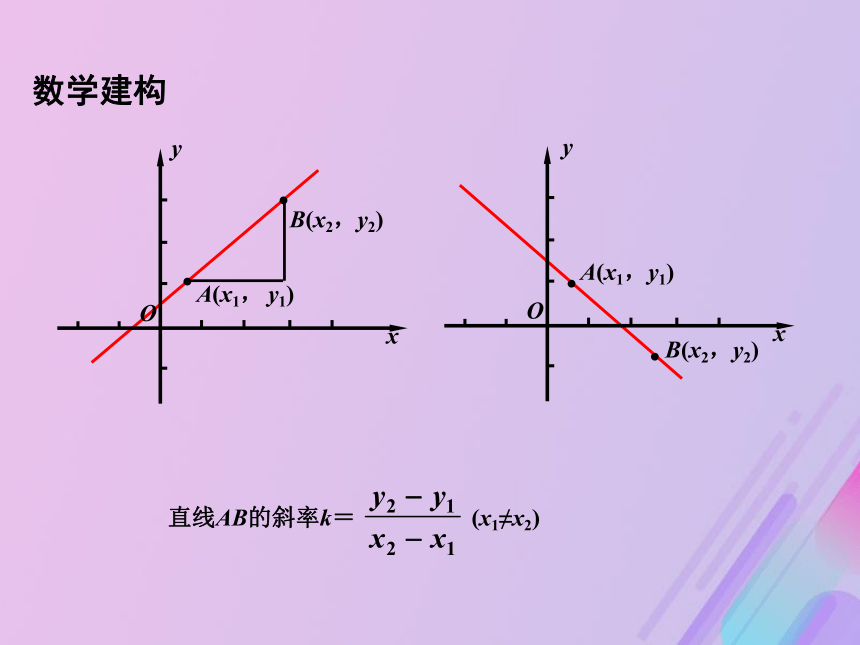
如上图,山坡PQ的坡度即为用坡度来刻画直线的倾斜程度.Fxy如图,建立直角坐标系,则O(0,0), A(300,100), B(600,250)直线OA的斜率k=直线AB的斜率k=数学建构直线AB的斜率k=A(x1, y1)OxyB(x2,y2)yA(x1,y1)OxB(x2,y2)(x1≠x2) 数学建构3. 直线AB的斜率与所选择直线上两点的位置无
关.定直线的斜率是确定的. 2. 直线AB的斜率与A,B两点的顺序无关.1.x1≠x2,若 x1=x2 ,即直线垂直于x轴,此
时,斜率不存在. 数学建构例1 如图,直线l1 ,l2 , l3都经过点P(3,2),又分别过点Q1(-2,-1)、Q2(2,6) , Q3(-3,2), 试计算直线 l1 , l2 , l3的斜率.解: 设k1、k2、k3分别表示直线l1 、l2、l3的斜率,
则 k2=-4, k3=0, (1)当直线的斜率为正时,直线从左下方向右上方倾斜(l1);由图可以看出(2)当直线的斜率为负时,直线从左上方向右下方倾斜(l2);(3)当直线的斜率为0时,直线与x轴平行或重合(l3).反之也成立. 数学应用 解: 故A , B , C 三点共线.已知三点A(-1,4)、B(2,1)、 C(-2,5),判断这三点是否共线?数学应用变式:若三点A(4,5) , B(-2a,-3) , C(1,a)共线,则a=________.小结:若三点A(4,5) , B(-2a,-3) , C(1,a)共线,则a=________.例2 经过点P(3,2)画直线,且使直线的斜率分别为: 解:(1)直线l1即为所求.(2)直线l2即为所求.P数学应用①与x轴相交的直线;
②绕交点按逆时针方向旋转;
③最小正角;
④规定:与x轴平行或重合的直线倾斜角为0?;
⑤{? |0?≤?<180?}. 直线的倾斜角和直线的斜率一样,也是刻画直线倾斜程度的量,但直线的倾斜角侧重于直观形象,直线的斜率则侧重于数量关系.
任何直线都有倾斜角,但不是任何直线都有斜率.数学建构直线的倾斜角①与x轴垂直的直线斜率不存在,倾斜角为90?;
②一条与x轴不垂直的定直线斜率为定值;
③k=tan?.数学建构直线的倾斜角与斜率的关系:④ tan?=-tan(180?-?);
⑤ ?=0?时,k=0;
0?<?<90? 时,k>0,且k随着?的增大而增大;
?=90?时,k不存在;
90?<?<180?时,k<0,且k随着?的增大而增大.例3 根据下列条件,分别画出经过点P,且斜率为k的直线,并写出倾斜角?: 数学应用(1)P(1,2),k=1; (2)P(-1,3),k=0;
(3)P(0,-2),k= ;(4)P(1,2),斜率不存在. 作业:P80练习1,2,3,5.
如上图,山坡PQ的坡度即为用坡度来刻画直线的倾斜程度.Fxy如图,建立直角坐标系,则O(0,0), A(300,100), B(600,250)直线OA的斜率k=直线AB的斜率k=数学建构直线AB的斜率k=A(x1, y1)OxyB(x2,y2)yA(x1,y1)OxB(x2,y2)(x1≠x2) 数学建构3. 直线AB的斜率与所选择直线上两点的位置无
关.定直线的斜率是确定的. 2. 直线AB的斜率与A,B两点的顺序无关.1.x1≠x2,若 x1=x2 ,即直线垂直于x轴,此
时,斜率不存在. 数学建构例1 如图,直线l1 ,l2 , l3都经过点P(3,2),又分别过点Q1(-2,-1)、Q2(2,6) , Q3(-3,2), 试计算直线 l1 , l2 , l3的斜率.解: 设k1、k2、k3分别表示直线l1 、l2、l3的斜率,
则 k2=-4, k3=0, (1)当直线的斜率为正时,直线从左下方向右上方倾斜(l1);由图可以看出(2)当直线的斜率为负时,直线从左上方向右下方倾斜(l2);(3)当直线的斜率为0时,直线与x轴平行或重合(l3).反之也成立. 数学应用 解: 故A , B , C 三点共线.已知三点A(-1,4)、B(2,1)、 C(-2,5),判断这三点是否共线?数学应用变式:若三点A(4,5) , B(-2a,-3) , C(1,a)共线,则a=________.小结:若三点A(4,5) , B(-2a,-3) , C(1,a)共线,则a=________.例2 经过点P(3,2)画直线,且使直线的斜率分别为: 解:(1)直线l1即为所求.(2)直线l2即为所求.P数学应用①与x轴相交的直线;
②绕交点按逆时针方向旋转;
③最小正角;
④规定:与x轴平行或重合的直线倾斜角为0?;
⑤{? |0?≤?<180?}. 直线的倾斜角和直线的斜率一样,也是刻画直线倾斜程度的量,但直线的倾斜角侧重于直观形象,直线的斜率则侧重于数量关系.
任何直线都有倾斜角,但不是任何直线都有斜率.数学建构直线的倾斜角①与x轴垂直的直线斜率不存在,倾斜角为90?;
②一条与x轴不垂直的定直线斜率为定值;
③k=tan?.数学建构直线的倾斜角与斜率的关系:④ tan?=-tan(180?-?);
⑤ ?=0?时,k=0;
0?<?<90? 时,k>0,且k随着?的增大而增大;
?=90?时,k不存在;
90?<?<180?时,k<0,且k随着?的增大而增大.例3 根据下列条件,分别画出经过点P,且斜率为k的直线,并写出倾斜角?: 数学应用(1)P(1,2),k=1; (2)P(-1,3),k=0;
(3)P(0,-2),k= ;(4)P(1,2),斜率不存在. 作业:P80练习1,2,3,5.
