2018年高中数学第2章平面解析几何初步2.1.5平面上两点间的距离课件3苏教版必修2(14张)
文档属性
| 名称 | 2018年高中数学第2章平面解析几何初步2.1.5平面上两点间的距离课件3苏教版必修2(14张) |  | |
| 格式 | zip | ||
| 文件大小 | 437.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-23 08:33:12 | ||
图片预览



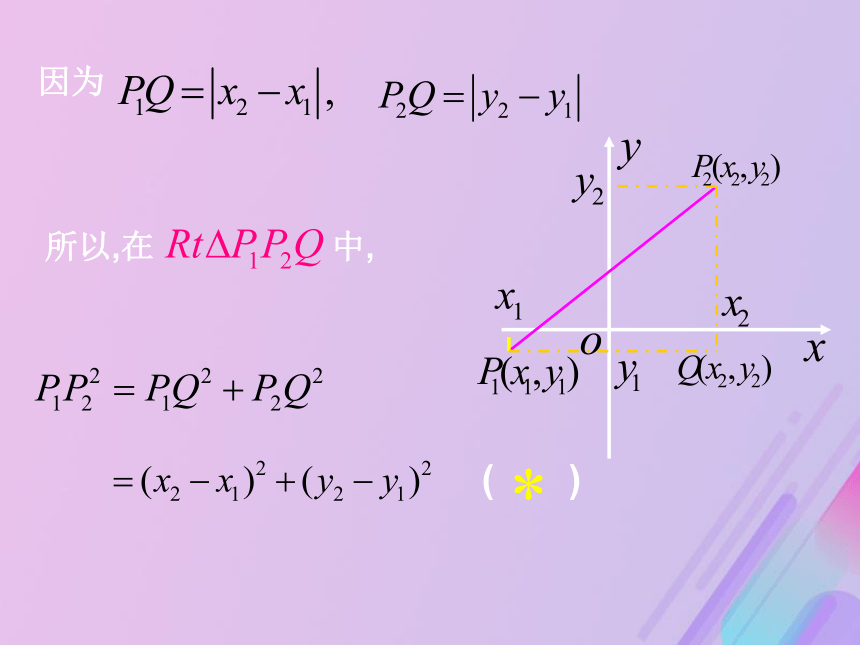


文档简介
课件14张PPT。平面上两点间的距离 已知四点A(-1,3),B(3,-2),
C(6,-1),D(2,4),则四边形ABCD
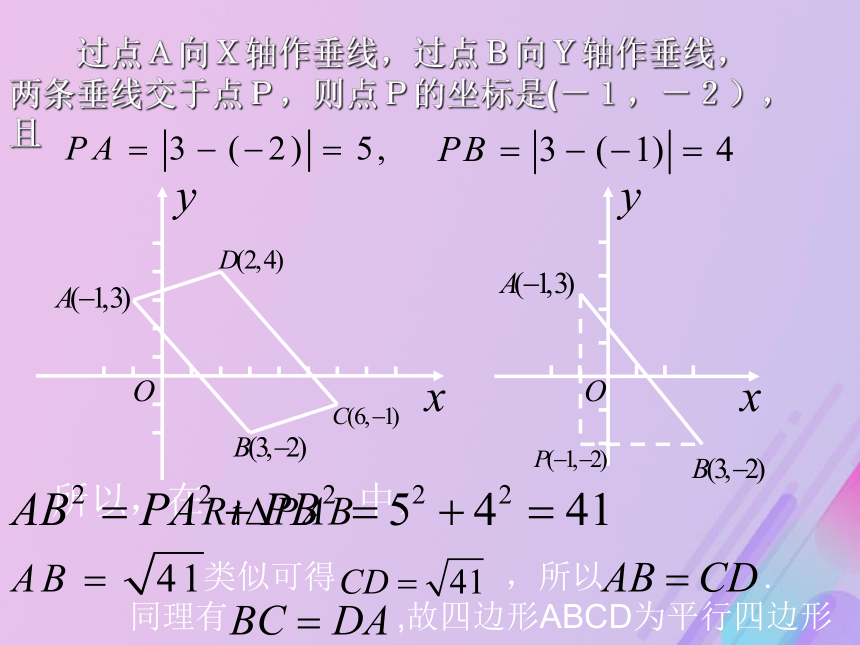
是否为平行四边形?分析:如何判断一个四边形是否为平行四边形?1.判断两组对边是否对应平行2.判断一组对边是否平行且相等问题:如何计算两点间的距离?3.对角线互相平分的四边形为平行四边形 过点A向X轴作垂线,过点B向Y轴作垂线,
两条垂线交于点P,则点P的坐标是(-1,-2),
且因此,A,B间的距离合作探究分析:利用距离公式例1例题讲解现在再来考察本节开头的问题,由于两条对角线互相平分的四边形是平行四边形,所以,只需说明对角线AC和BD的中点相同,即可推得四边形ABCD为平行四边形.那怎样求线段AC中点的坐标呢?此即中点坐标公式中点坐标公式的证明可仿照上例的推导过程加以证明,亦可用距离公式及斜率公式证明.分析:1.先利用中点坐标公式求出点M的坐标,3.可利用两点式求中线AM所在直线的方程2.再利用两点间距离公式求得中线AM的长
例2.例3由两点间距离公式易证得分析:练 习P92练习 1,2,3小 结:
C(6,-1),D(2,4),则四边形ABCD
是否为平行四边形?分析:如何判断一个四边形是否为平行四边形?1.判断两组对边是否对应平行2.判断一组对边是否平行且相等问题:如何计算两点间的距离?3.对角线互相平分的四边形为平行四边形 过点A向X轴作垂线,过点B向Y轴作垂线,
两条垂线交于点P,则点P的坐标是(-1,-2),
且因此,A,B间的距离合作探究分析:利用距离公式例1例题讲解现在再来考察本节开头的问题,由于两条对角线互相平分的四边形是平行四边形,所以,只需说明对角线AC和BD的中点相同,即可推得四边形ABCD为平行四边形.那怎样求线段AC中点的坐标呢?此即中点坐标公式中点坐标公式的证明可仿照上例的推导过程加以证明,亦可用距离公式及斜率公式证明.分析:1.先利用中点坐标公式求出点M的坐标,3.可利用两点式求中线AM所在直线的方程2.再利用两点间距离公式求得中线AM的长
例2.例3由两点间距离公式易证得分析:练 习P92练习 1,2,3小 结:
