2018年高中数学第2章平面解析几何初步2.1.6点到直线的距离课件4苏教版必修2(16张)
文档属性
| 名称 | 2018年高中数学第2章平面解析几何初步2.1.6点到直线的距离课件4苏教版必修2(16张) |

|
|
| 格式 | zip | ||
| 文件大小 | 320.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-23 00:00:00 | ||
图片预览





文档简介
课件16张PPT。点到直线的距离已知A(-1,3),B(3,-2),C(6,-1),D(2,4)
问题1:四边形ABCD是否为平行四边形?
问题2:如何计算它的面积?
E一 问题情境:大家觉得如何求点D到直线AB的距离呢?思考:方法1 通过求点E的坐标,用两点间距离公式求DE第二步 写出DE所在直线的方程 第一步 由DE垂直AB,可知DE所在直线的斜率为第三步 由AB和DE所在直线方程联立方程组
第四步 利用两点间距离公式,求出点D到直线AB的距离
解得垂足E的坐标二 建构数学:方法2 如图,过点D作x轴的平行线,交直线AB于M,
过点D作y轴的平行线,交直线AB于N,
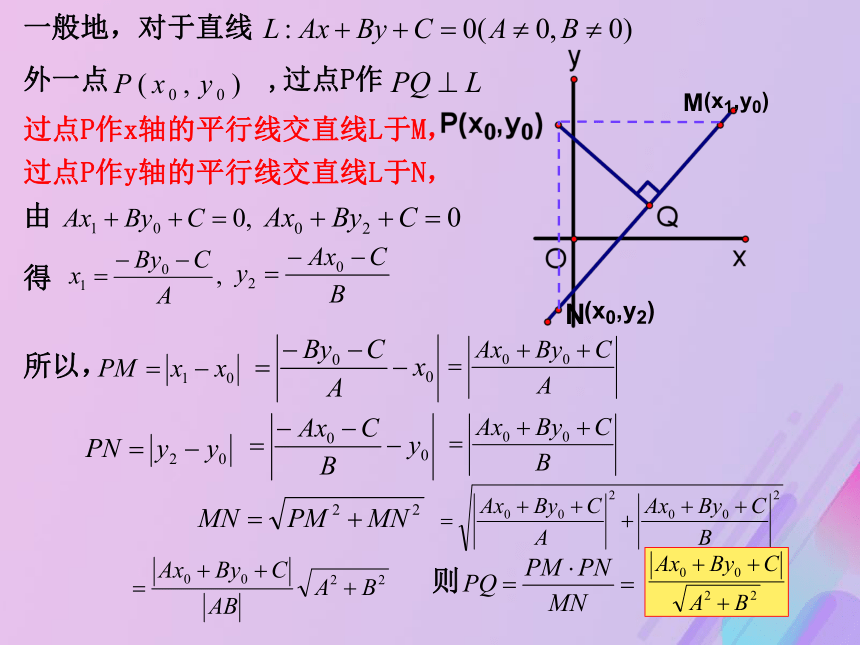
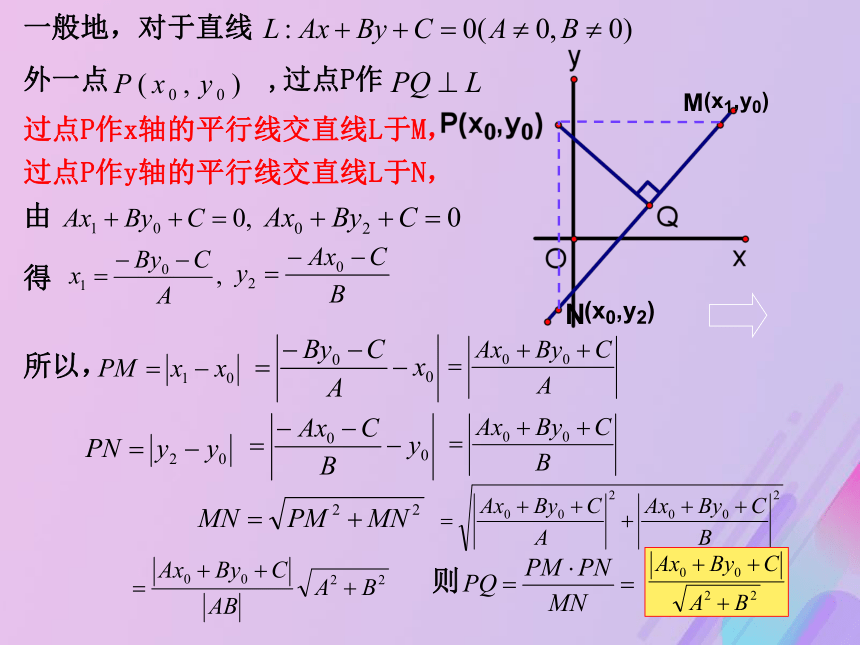
第一步 求出第二步 计算MN第三步 计算第四步 求出一般地,对于直线
外一点 ,过点P作 过点P作x轴的平行线交直线L于M,
过点P作y轴的平行线交直线L于N,
由得 所以,则一般地,对于直线
外一点 ,过点P作 过点P作x轴的平行线交直线L于M,
过点P作y轴的平行线交直线L于N,
由得 所以,则 由此,我们得到,点 到直线
的距离为思考:(1)当A=0或B=0时,该公式是否仍适用? 由此,我们得到,点 到直线
的距离为(2)你还能通过其他途径求点P到直线L的距离吗?思考:(1)当A=0或B=0时,该公式是否仍适用?三 数学运用例1、求点P(-1,2)到下列直线的距离:解:(1)根据点到直线的距离公式,得(2)注意:(1)直线方程必须化为一般式;(2)当A=0或B=0时,公式仍适用例2 求两条平行直线 与
之间的距离解:在直线 上取点P(4,0),则点P(4,0)到直线 距离d就是两条平行直线之间的距离所以,两条平行线间的距离为d一般地,已知两条平行直线怎样求直线 和 之间的距离呢?设 为直线 上一点,则 到 的距离则思考:解:(1)(2)直线 化为 ,
再化为所以,(2) 与(1)直线方程必须为一般式(2)两直线 和 的系数必须保持一致 注意:四 课堂小结:1.点到直线的距离:2.两平行直线之间的距离:五 课后作业:1.尝试用其他方法推导点到直线的距离公式2.完成书本课后习题
问题1:四边形ABCD是否为平行四边形?
问题2:如何计算它的面积?
E一 问题情境:大家觉得如何求点D到直线AB的距离呢?思考:方法1 通过求点E的坐标,用两点间距离公式求DE第二步 写出DE所在直线的方程 第一步 由DE垂直AB,可知DE所在直线的斜率为第三步 由AB和DE所在直线方程联立方程组
第四步 利用两点间距离公式,求出点D到直线AB的距离
解得垂足E的坐标二 建构数学:方法2 如图,过点D作x轴的平行线,交直线AB于M,
过点D作y轴的平行线,交直线AB于N,
第一步 求出第二步 计算MN第三步 计算第四步 求出一般地,对于直线
外一点 ,过点P作 过点P作x轴的平行线交直线L于M,
过点P作y轴的平行线交直线L于N,
由得 所以,则一般地,对于直线
外一点 ,过点P作 过点P作x轴的平行线交直线L于M,
过点P作y轴的平行线交直线L于N,
由得 所以,则 由此,我们得到,点 到直线
的距离为思考:(1)当A=0或B=0时,该公式是否仍适用? 由此,我们得到,点 到直线
的距离为(2)你还能通过其他途径求点P到直线L的距离吗?思考:(1)当A=0或B=0时,该公式是否仍适用?三 数学运用例1、求点P(-1,2)到下列直线的距离:解:(1)根据点到直线的距离公式,得(2)注意:(1)直线方程必须化为一般式;(2)当A=0或B=0时,公式仍适用例2 求两条平行直线 与
之间的距离解:在直线 上取点P(4,0),则点P(4,0)到直线 距离d就是两条平行直线之间的距离所以,两条平行线间的距离为d一般地,已知两条平行直线怎样求直线 和 之间的距离呢?设 为直线 上一点,则 到 的距离则思考:解:(1)(2)直线 化为 ,
再化为所以,(2) 与(1)直线方程必须为一般式(2)两直线 和 的系数必须保持一致 注意:四 课堂小结:1.点到直线的距离:2.两平行直线之间的距离:五 课后作业:1.尝试用其他方法推导点到直线的距离公式2.完成书本课后习题
