2018年高中数学第2章平面解析几何初步2.2.2直线与圆的位置关系课件5苏教版必修2(16张)
文档属性
| 名称 | 2018年高中数学第2章平面解析几何初步2.2.2直线与圆的位置关系课件5苏教版必修2(16张) |

|
|
| 格式 | zip | ||
| 文件大小 | 260.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-23 08:35:25 | ||
图片预览




文档简介
课件16张PPT。直线和圆的位置关系
·直线和圆的位置关系掌握直线和圆的位置关系及其研究方法:
1、几何特征—数形结合法2、代数特征—方程组解的个数复习目标:直线和圆的位置关系知识点梳理:几何特征代数特征1、直线x-y-1=0与圆x2+y2=4的位置关系是:______。 (1)直线x-y+m=0与圆x2+y2=4的相交,求m 的取值范
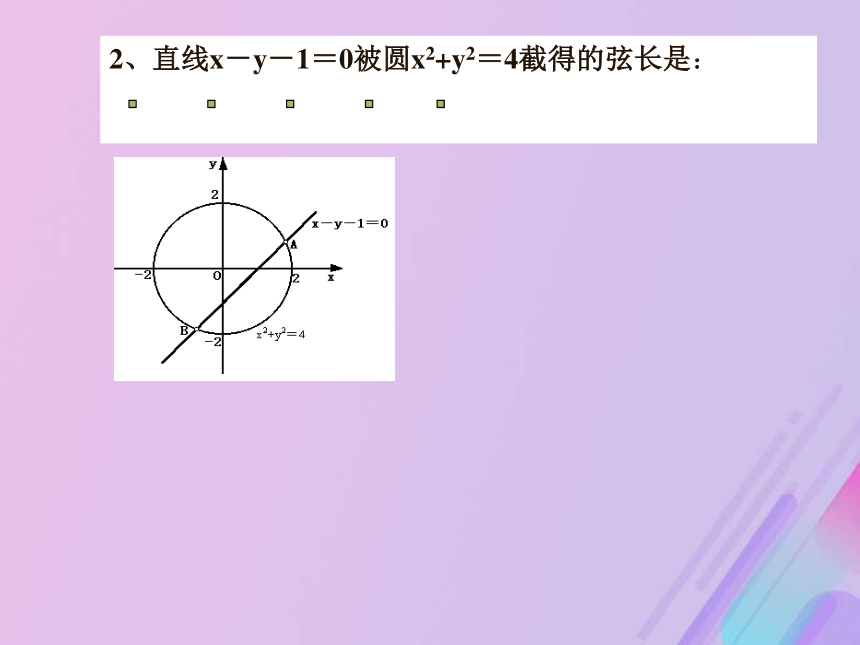
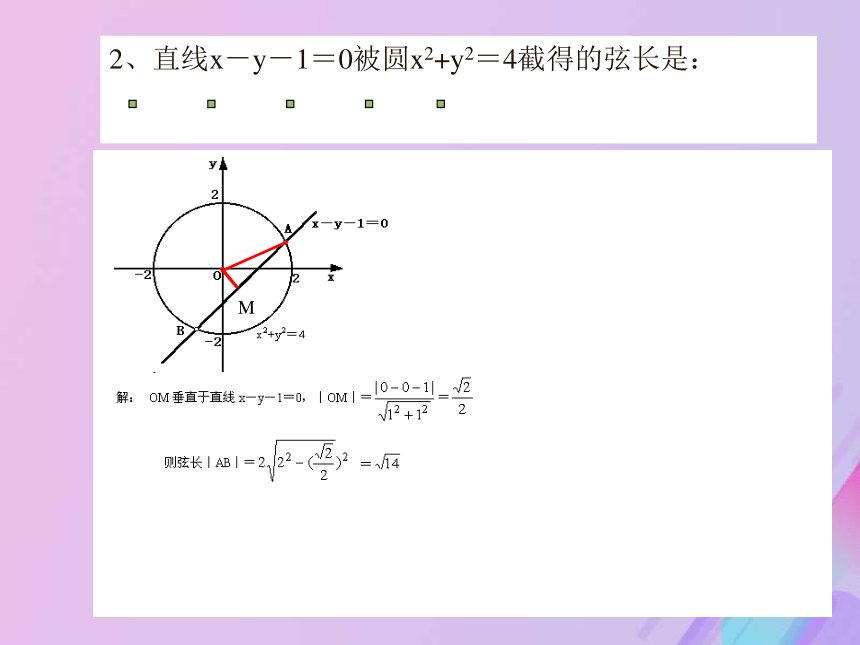
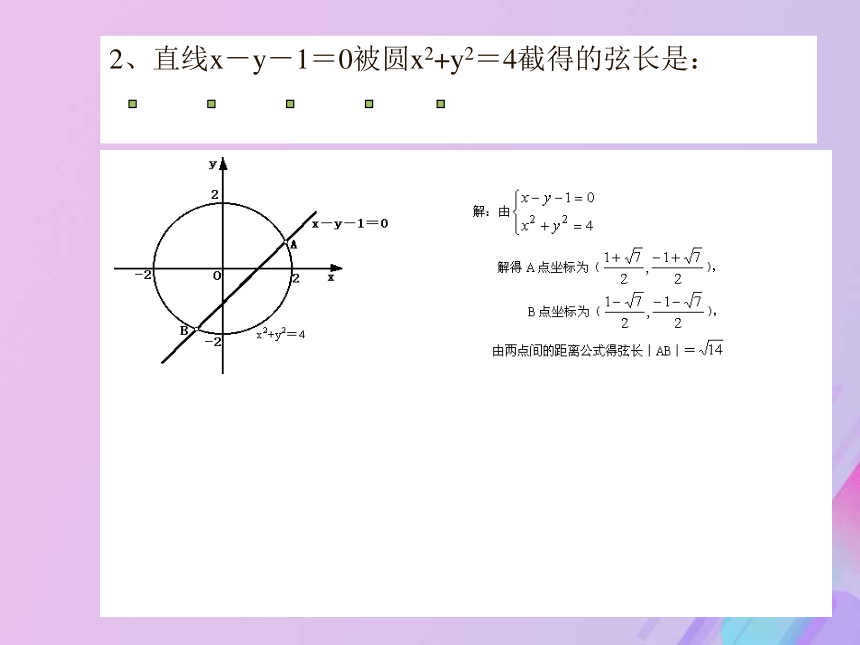
围:_____。 变题(2)直线x-y+m=0与圆x2+y2=4的相切,求m 的值:__; (3)直线x-y+m=0与圆x2+y2=4的相离,求m 的取值范围:______________________。 相交练习 :直线5x+12y-8=0与圆x2-2x+y2+6y+2=0的位置关系是___________.相离2、直线x-y-1=0被圆x2+y2=4截得的弦长是: 2、直线x-y-1=0被圆x2+y2=4截得的弦长是: M2、直线x-y-1=0被圆x2+y2=4截得的弦长是: 2、直线x-y-1=0被圆x2+y2=4截得的弦长是: 2、直线x-y-1=0被圆x2+y2=4截得的弦长是: 因为M(x0,y0)在圆上,所以x02+y02=r2,所求切线方程是3、已知圆的方程是x2+y2=r2,求经过圆上一点M(x0,y0)的切线的方程.
解:如图,设切线的斜率为k,半径OM的斜率为k1.因
为圆的切线垂直于过切点的半径,于是k=- .
经过点M的切线方程是整理得 x0x+y0y=x02+y02.x0x+y0y=r2当点M在坐标轴上时,可以验证上面方程同样适用3、已知圆的方程是x2+y2=r2,求经过圆上一点M(x0,y0)的切线的方程.
解:如图,设P为该切线上一点,因为M(x0,y0)在圆上,所以x02+y02=r2,所求切线方程是整理得 x0x+y0y=x02+y02.x0x+y0y=r24、直线3x+4y+m=0与圆x2+y2-5y=0交于两点A、B,且OA OB(O为原点),求m的值.
4、直线3x+4y+m=0与圆x2+y2-5y=0交于两点A、B,且OA OB(O为原点),求m的值. 解:
4、直线3x+4y+m=0与圆x2+y2-5y=0交于两点A、B,且OA OB(O为原点),求m的值. 解:设直线与圆的交点为A(x1,y1)和B(x2,y2),
练习1、过点P(6,-4)被圆x2+y2=20 截得的弦长是6 的弦所在的直线方程是____________;2、由点P(1,3)引圆x2+y2=9的切线长是__________3、直线mx+y+m+1=0与圆x2+y2=2的位置关系 是____________;直线和圆的位置关系小结:几何特征代数特征
·直线和圆的位置关系掌握直线和圆的位置关系及其研究方法:
1、几何特征—数形结合法2、代数特征—方程组解的个数复习目标:直线和圆的位置关系知识点梳理:几何特征代数特征1、直线x-y-1=0与圆x2+y2=4的位置关系是:______。 (1)直线x-y+m=0与圆x2+y2=4的相交,求m 的取值范
围:_____。 变题(2)直线x-y+m=0与圆x2+y2=4的相切,求m 的值:__; (3)直线x-y+m=0与圆x2+y2=4的相离,求m 的取值范围:______________________。 相交练习 :直线5x+12y-8=0与圆x2-2x+y2+6y+2=0的位置关系是___________.相离2、直线x-y-1=0被圆x2+y2=4截得的弦长是: 2、直线x-y-1=0被圆x2+y2=4截得的弦长是: M2、直线x-y-1=0被圆x2+y2=4截得的弦长是: 2、直线x-y-1=0被圆x2+y2=4截得的弦长是: 2、直线x-y-1=0被圆x2+y2=4截得的弦长是: 因为M(x0,y0)在圆上,所以x02+y02=r2,所求切线方程是3、已知圆的方程是x2+y2=r2,求经过圆上一点M(x0,y0)的切线的方程.
解:如图,设切线的斜率为k,半径OM的斜率为k1.因
为圆的切线垂直于过切点的半径,于是k=- .
经过点M的切线方程是整理得 x0x+y0y=x02+y02.x0x+y0y=r2当点M在坐标轴上时,可以验证上面方程同样适用3、已知圆的方程是x2+y2=r2,求经过圆上一点M(x0,y0)的切线的方程.
解:如图,设P为该切线上一点,因为M(x0,y0)在圆上,所以x02+y02=r2,所求切线方程是整理得 x0x+y0y=x02+y02.x0x+y0y=r24、直线3x+4y+m=0与圆x2+y2-5y=0交于两点A、B,且OA OB(O为原点),求m的值.
4、直线3x+4y+m=0与圆x2+y2-5y=0交于两点A、B,且OA OB(O为原点),求m的值. 解:
4、直线3x+4y+m=0与圆x2+y2-5y=0交于两点A、B,且OA OB(O为原点),求m的值. 解:设直线与圆的交点为A(x1,y1)和B(x2,y2),
练习1、过点P(6,-4)被圆x2+y2=20 截得的弦长是6 的弦所在的直线方程是____________;2、由点P(1,3)引圆x2+y2=9的切线长是__________3、直线mx+y+m+1=0与圆x2+y2=2的位置关系 是____________;直线和圆的位置关系小结:几何特征代数特征
